III Предел функции
Определение 3.1
Число
называется
пределом функции при 
стремящемся
к
,
если какую бы последовательность {
},
сходящуюся к
мы ни взяли, соответствующая
последовательность функций стремится
к
.
Итак,
если 
,
то 
(3.1)
Если
мы возьмем две последовательности,
сходящиеся к 
а соответствующие последовательности
функций сходятся к разным пределам
,
то предела у функции в этой точке не
существует.
Покажем это на примерах.
Пример 3.1
не существует
Возьмем
последовательности 
= 5 + 
= 
= 
при 
= 5
-
, 
= 
= 
при
Пример 3.2
Рассмотрим предел
Вновь возьмем две последовательности
= 
= 
= 
= 
то есть на разных последовательностях стремящихся к нулю, предел последовательности функций будет разным.
Следовательно, не существует.
Так как мы сформулировали определение предела функции в точке на «на языке последовательности», то арифметические свойства предела числовой последовательности будут справедливы и для предела функции в точке.
Пусть
, 
Тогда:
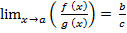если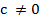 
если
Замечательные пределы
= 
(3.2)
Доказательство
проведем для
> 0. Для
< 0 доказательство аналогичное путем
замены –
=
Итак, любое положительное число можно заключить между двумя натуральными числами
Запишем очевидную цепочку неравенств
(3.2)
Преобразуем эти неравенства так, чтобы мы могли воспользоваться пределом (2.10)
Применяя (2.7), получим
=
Этот предел можно записать в следующих формах
=
(3.3)
= 
замена 
Этот предел можно применить для вычисления следующих пределов.
Покажем, что:
= 1 (3.4)
= 
= 
=
(по свойству логарифма степени)
Вычислим
,
сделаем замену
, 
,
=
= 1 (с учетом 3.4)
Рассмотрим применение формулы
=
Пусть
банк начисляет проценты на вклады каждый
день исходя из заданной ставки годового
процента 
.
Вклад 
по будням будет расти следующим образом
, 
…….
,
Поэтому
банк должен будет выплатить через год
Так,
если
= 0,5 то 
При
этом оказывается ,что это превосходит
сумму 
,
которую банк обязуется выплатить клиенту
через год, исходя из ставки
годового процента. Значит, при непрерывном
исчислении процентов надо исходить из
заниженной ставки q
годового процента, так чтобы 
.Так при
= 0,5 
0,
375
IV Непрерывность функции
Пусть
функция определена в области 
–
произвольная точка этой области 
.
Определение 4.1
Функция
называется непрерывной в точке
,
если предел функции в этой точке
существует и равен значению функции в
этой точке
(4.1)
Дадим еще одно определение
Обозначим
- приращение функции в точке
Определение 4.2
Функция
называется
непрерывной в точке
,
если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
Покажем, как работает это определение на некоторых функциях.
Примеры
= 2 
|
= |
Итак,
, то 
- 
= 2 
+ 
, то
Исходя из определения (4.1), мы видим, что арифметические действия не выводят из класса непрерывных функций.
Определение 4.3
Функция называется непрерывной в области, если она непрерывна в произвольной точке этой области.
Теорема 4.1
Все элементарные функции непрерывны в области определения.
Приведем некоторые свойства непрерывных функций.
Теорема 4.2
Пусть
функция 
непрерывна в точке 
и 
,
тогда существует окрестность этой
точки, в которой функция сохраняет знак.
Из
определения предела следует, что для
любого 
существует, что для точки
,
в которой выполняется неравенство
(4.2)
Пусть
для определенности 
> 0. В силу произвольности
это число можно взять таким, что 
>
0 тогда из неравенство (4.2) и следует
теорема 4.2.
Теорема 4.3
Пусть
функция
непрерывна на отрезке [a,b]
и на концах этого отрезка принимает
значения разных знаков. Тогда обязательно
найдется точка
из данного интервала, в которой функция
обращается в нуль, то есть
(4.3)
Доказательство проведем конструктивно.
Разделим отрезок [a,b] пополам.
Можем
сразу попасть с точку 
.
Пусть будет не так. Тогда выберем тот
из двух образовавшихся сегментов тот,
на концах которого функция принимает
значение разных обозначим его [
,
].
Вновь проделаем предыдущую процедуру.
Получим последовательность отрезков
[
,
],
[
,
],
…………..[
,
],
обладающую следующими свойствами
,
,
Длина отрезков равна
,
так как последовательности концов образуют монотонные и ограниченные последовательности,
то
(4.4)
Пусть
для определенности 
и 
то
из теоремы 4.2 следует 
0 или
0, откуда
= 0
Этот алгоритм можно запрограммировать для нахождения корня уравнения
= 0 (4.5)
Вычислить пределы
Вопросы для самоподготовки
Сходится ли монотонная последовательность? Приведите примеры, иллюстрирующие ответ.
Будет ли последовательность бесконечно большой, если она не ограничена? Привести примеры
Указать, какие из приведенных ниже последовательностей
а) сходятся;
б) ограничены;
в) являются бесконечно малыми;
г) являются бесконечно большими;
, 
, 
, 
Можно ли утверждать, что произведение бесконечно большой последовательности на бесконечно малую будет:
а) бесконечно большой;
б) бесконечно малой;
в) сходящейся;
г) ограниченной.
Привести соответствующие примеры.