Лабораторна робота № 2 вивчення механічного осцилятора з одним ступенем вільності

Мета роботи – ознайомитися з характером коливань; розрахувати основні характеристики механічного осцилятора, що зумовлюють процес коливань.

Прилади та обладнання: штатив зі шкалою, пружиною і тягарцем масою m; секундомір; освітлювач.

Теоретичні відомості

У механіці найпростішим осцилятором з одним ступенем вільності є пружинний маятник – тіло масою m, що підвішене на невагомій абсолютно пружній пружині довжиною l.

На рис.1 показано тягарець m, підвішений до пружини l, який перебуває у спокої. В цьому положенні на нього діють сили тяжіння ( ) та пружності ( ). При цьому відповідно до закону Гука, маємо:

д

Рис. 1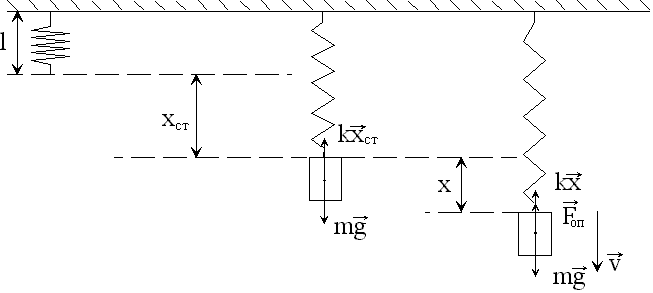

е x_ст – статична деформація пружини.

Охарактеризуємо зміщення тіла від стану рівноваги координатою x, причому вісь x спрямуємо вздовж вертикалі вниз, а нуль осі з’єднаємо з положенням рівноваги тіла.

Якщо вивести тіло з положення рівноваги, подовживши пружину на величину x вниз (рис.1) зовнішньою силою, то в пружині виникне додаткова сила пружності , де – вектор зміщення тіла. Якщо після цього припинити дію зовнішньої сили , то в системі пружина–тіло виникне коливний рух. За другим законом Ньютона, маємо:

. (1).

Так як прискорення .

Тоді

.

Приймемо позначення і отримуємо диференційне рівняння незгасаючих коливань пружинного маятника

(2)

з розв’язком

, (3)

де x – зміщення тягарця m від положення рівноваги, x₀ – амплітуда коливань, ₀ – початкова фаза.

В реальних умовах при коливаннях необхідно приймати до уваги опір середовища. Для малих швидкостей руху сила опору середовища , де r – коефіцієнт опору.

Тоді рівняння руху набуває вигляду:

,

або

.

Введемо позначення і дістанемо диференційне рівняння згасаючих коливань пружинного маятника: (4)

з розв’язком

, (5)

де x₀ – початкова амплітуда коливань, – амплітуда згасаючих коливань у момент часу t , e – основа натуральних логарифмів,  – коефіцієнт згасання. Графік цих коливань показаний на рис. 2.

Маса тягарця m, коефіцієнт опору r і жорсткість пружини k називаються параметрами осцилятора (коливальної системи), що розглядається, а величини x₀ і ₀ є константи, які визначаються початковими умовами.

Циклічна частота власних коливань маятника (при =0 – н

Рис. 2

езгасаючі коливання) ,

звідки період власних коливань .

Циклічна частота згасаючих коливань пружинного маятника

.

Внаслідок згасання такі коливання не є суворо періодичними. Тому під їх періодом розуміють інтервал часу між двома послідовними максимальними відхиленнями від положення рівноваги в один бік.

Період згасаючих коливань

.

Логарифмічний декремент згасання  характеризує згасання (зменшення амплітуди) за один період і визначається як натуральний логарифм відношення двох амплітуд, які рознесені в часі через період T_З

.

Для N коливань .

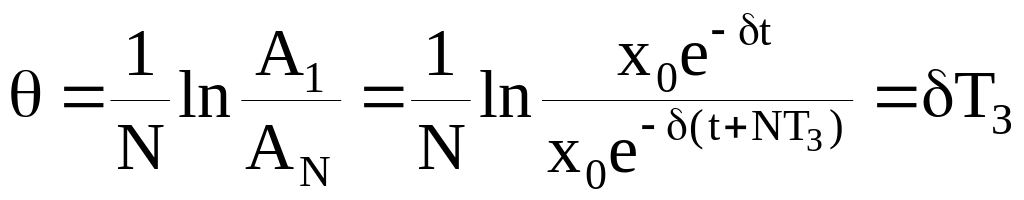Часом релаксації  називається проміжок часу, за який амплітуда коливань зменшується в e разів. Оскільки , то =1, або , тобто час релаксації  є обернено пропорційний коефіцієнту згасання коливань.

Якщо ввести N_e – число коливань, за яке амплітуда осцилятора зменшується в e разів, то =T_ЗN_e і логарифмічний декремент згасання

.

Для характеристики коливних систем вводиться поняття добротності системи Q: .

При малих згасаннях (  ₀ ) період згасаючих коливань T_З дорівнює періоду власних коливань, тобто T₀ , тому

.

Таким чином, чим більша добротність системи, тим повільніше затухають коливання.