5 Расчет и конструирование колонны

Верхняя часть ступенчатой колонны обычно проектируется сплошной, двутаврового сечения, нижняя часть принимается сплошной при ширине до 1 м, а при большей ширине ее экономичнее делать сквозного сечения.

В раме ригель имеет жесткое крепление, поэтому для подбора симметричного сечения верхней части колонны расчетная комбинация усилий М, N устанавливается по сечению 1-1. Для подбора несимметричного сечения сплошной или сквозной нижней части следует рассмотреть несколько возможных комбинаций усилий: расчетные комбинации с + М в нижнем сечении колонны, при котором изгибающий момент догружает наружную ветвь и с -М в сечении под уступом, здесь изгибающий момент догружает подкрановую ветвь.

Расчетные длины верхней и нижней частей колонны в плоскости рамы

l_ef= μ * 1.

В большинстве случаев при 0,3 ≥I_в/I_н ≥ 0,05, Н_в/Н_н ≤0,6, N_в/N_н ≥ 3, поэтому μ_в= 3 > μ_н=2.

Материал колонны – сталь С235, при толщине листового проката t£20 мм, Rу=230Мпа

Так как Н_в/Н_н = 4000/10200=0,392< 0,6;

N_н/N_в=684,42/153,36=4,46> 3; и

I_в/I_н=0,1 принимаем m_в = 3, m_н = 2

Расчетные длины для нижней и верхней частей колонны в плоскости рамы

l_efx^н =Н_н · m_н =10.2*2.0 =20.4 м;

l_efx^в = Н_в · m_в = 4.0*3,0=12 м.

Расчетные длины колонны из плоскости рамы

l_efу^в = Н_в – h_б =4.0-1=3.0 м.

l_efу^н = Н_н=10.2 м.

Подбор и проверка сечений верхней (надкрановой ) части колонны

Расчетная комбинация усилий: М_max, N_соотв.(сечение 1-1, нагрузки 1,2,3*,4(-М),5*

М= -350.49 кН, N= - 153.36кН

е_х= М / N = 350.49/153.36=2.29м .

Подбор сечения колонны из условия устойчивости в плоскости действия момента. Требуемая площадь сечения

А_тр= N /(j_еRуg_с),

Здесь g_с =1,0; j_е = f(l_x,m);

`l_x = l_x Ö R_у/E; l_x= l_efx^в / i_x.

Для симметричного двутавра

i_x =0,42 * h=0,42* 50=21 см; lx =1200/21=57: l_x = 57* Ö230/(21х10⁴)= 1.83

ядровое расстояние r_x=0,35* h =0,35х50=17.5 см

Относительный эксцентриситет m_x=e_x/r_x=229/17.5=13.09

Предварительно прием A_f\A_w³1,0 .

При 0£`l £ 5 и 5< m £20

h=1,4-0,02`l= 1,4-0,02*1.85=1.36

Приведенный эксцентриситет

m_ef=hm_x=1,36*13.06=17.8

При`l_x = 1.88 и m_ef =17.8 j_е =0.097

Требуемая площадь сечения

A_тр=N/(j_eR_yg_c)=153.36*10/(0,0762*230*1)= 87.5 см ²

Компоновка сечения

Предварительно принимаем толщину полок t_f =1.6см, тогда высота стенки колонны

h_w=h-2 t_f= 50-2*1.6=46.8 см.

Минимальная толщина стенки из условия местной устойчивости при `l>0,8

и m ³ 1 по [1] табл14.2.

t_{w min}=(h_w)/[(0,9+0,5`l) Ö(E/R_y)]=(46.8)/ [(0,9+0,5*1.88) Ö2,06х10⁵/230)] =0.84см.

Принимаем t_f =0,8 см (h_w / t_w =80/….120).

Включаем в расчетную площадь сечения колонны два крайних участка стенки шириной по

0,85 t_wÖ E/R_y =0,85х0,8хÖ20,6+10⁴ /230=21 см.

Расчетная площадь сечения стенки

A_w= 2*0,8*21=33.6 см²

Требуемая площадь полки

A_{f тр}=(A _тр-A_w)/2= (87.5-33.6)/2=27 см²

Из условия устойчивости верхней колонны из плоскости действия момента ширина полки

b_{f min}=l_efy^в/20=300/20=15 см

а из условия местной устойчивости сжатой полки

(b_ef/t_f) £ [(0,36+0,1`lх)Ö (E/R_y)]=(0,36+0,1*1.88)х Ö20,6х10⁴/230=16.6

где b_ef = (b_f-t_w)/ 2

Принимаем b_f = 22см; t_w =1,2см.

b_f /t_w =( b_f-t_w)/(2 x t_r)= (22-0,8)/(2*1.2)=8.83<16.6

A_f=22 x 1,2=26.4 см²

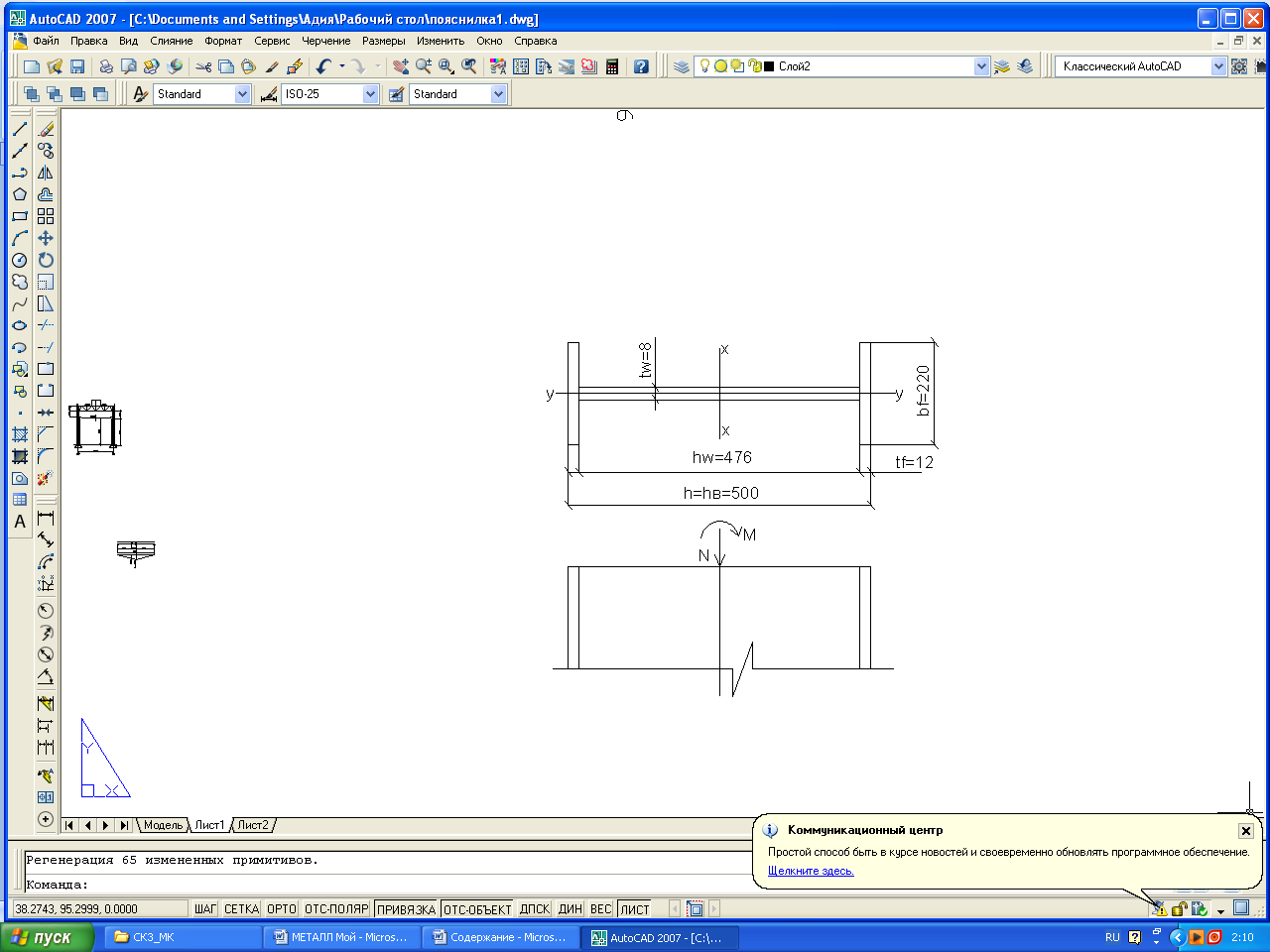
Рис.7 Сечение верхней (надкрановой) части колонны

Геометрические характеристики сечения

Полная площадь сечения A₀=2b_f t_f+h_w*t_w=2*22*1,6+47.6*0,8=90.88 см²

>А_ТР=113 см²

где h_w=h-2 t_f=50-2*1.2=47.6 см

Расчетная площадь сечения при учете только устойчивой части стенки

A= 2b_f x t_f +A_w =2*22.1.2+33.6=86.4 см²

При определении геометрических характеристик учитывается полно сечение

I_x= t_w h_w³/12 + 2 b_f t_f (h/2- t_f /2)²= 0,8*47.6³/12+2*22*1.2(50/2-1,2/2)²=

=38625см ⁴

I_y=2 t_f b_f³/12=2*1.2*22³/12 = 2129.6 см ⁴

W_x=I_x/0,5h=38625/25 =1545см³

r_x=W_x/A₀=1545 /90.88=17см

i_x=Ö I_x/A₀=Ö38625/99.88=21м

i_y=Ö I_y/A₀=Ö2129.6 /99.88=5 см

A_f/A_w= 26.4/0,8*47.6=0.7

Проверка устойчивости верхней части колонны в плоскости действия момента (относительно оси Х-Х)

l_x= l_efy^в/ i_x=1200/21=57

`l_x=l_хÖ E/R_y=57Ö230/(20,6*10 ⁴) =1.88

m_x=e_x/r_x=229/17=13.47

Так как A_f/A_w>1 (см. табл.7 приложения)

h=1,4-0,02 x `l_x =1,4-0,02*1.88=1.36

m_ef = hm_x = 1.36*13.47=18.35

Из табл.8 приложения находим j_е=0,0781

Проверим устойчивость сечения

б=N/(j_е A)=153.36*10/(0,0781*86.4) =227.27 МПа < Ry=230 МПа

Недонапряжение составляет

(230-227.27)/230х100=1.2%<5 %

Проверка устойчивости верхней части колонны из плоскости действия момента (относительно оси У-У)

Расчетный момент в сечении 2-2 соответствующий сочетанию нагрузок сечения 1-1 (1, 2, 3*,4(-М),5* )

М₂=-43.81-18.396+25.55-25.91-34.01=-96.58 кН м

Максимальный момент в пределах средней трети расчетной длины стержня

М_х=M₂ + (M₁-M₂)/H_в(H_в - l_efy^в/3 )=-96.58+(-350.49)-(-96.58)/4* (4-3/3)=238.72кНм

Значение М_х принимается не менее половины наибольшего по длине стержня момента

М_х=238.72 кНм > M_max/2=350.49/2=175.25 кНм

m_х = M_x A₀/(N W_x)=23872*90.88/(153.36*1545)=9 см

При m_x≤5

С=С₅=β/(1+α m_x)

где α и β – коэффициенты, принимаемые по табл. 10 (2).

При m_x≥10

С=С₁₀=1/(1+φ_у m_x/φ_в);

При 5 < m_x < 10

С=С₅(2 – 0.2*m_x) + C₁₀(0.2*m_x-1).

В данном расчете m_x=7,1. Принимая m_x=5 определим значение коэффициента α

α=0.65+0.05 m_x=0.65+0.05*5=0.9

λ_у=l_efу^в/i_у=300/5=60,

Так как λ_у=60< λ_с=95 в соответствии с табл. 10 β=1

С₅=β/(1+α m_x)=1/(1+0.9*5)=0.18

При λ_у=60 φ_у=0.811 (табл. 9 приложения)

Коэффициент снижения расчетного сопротивления при потере устойчивости балок в большинстве случаев при проверке колонн принимают φ_в=1.

С₁₀=1/(1+φ_у m_x/φ_в)=1/(1+10*0.811/1)=0,1

здесь принимают m_x=10.

С=С₅(2 – 0.2*m_x) + C₁₀(0.2*m_x-1)=0.18(2-0,2∙9)+0,1*(0.2*9-1)=0,116

h_w/t_w=47,6/0.8=59,5 <

поэтому в расчетное сечение включается полное сечение стенки.

б=N/(Сj_yA₀)=153,36*10/(0,116*0,811*90,88)=179 МПа< R_y=230 МПа

Подбор сечения нижней (подкрановой) части колонны

Расчетные комбинации усилий (сечения 3-3, 4-4)

М₁= -250,24кН, N₁= - 698,07кН (нагрузки (1,3,4 (-М));

М₂= 796,73 кН, N₂ = -684,42кН (нагрузки (1,2,3,4(+М));

Сечение нижней части колонны сквозное, состоящие из двух ветвей, соединенных решеткой. Подкрановую ветвь принимаем из широкополочного двутавра, а наружную – составного сварного сечения из трех листов.

Определим ориентировочное положение центра тяжести. Принимаем z₀=5см.

h₀=h_H - z₀=100-5=95 см

y₁=[çM₂ê/çM₁ç+çM₂ç]h₀=796,73/(250,24+796,73)*95=72см

у₂ = h₀ - у₁ = 95 – 72 =23 см.

Усилие в наружной ветви

N_в2=|N₂|у₁/h ₀+M₂/h ₀ =684,42*72/95 +79673/95=1357кН

Усилие в подкрановой ветви

N_в1=|N₁|у₂/h ₀+M₁/h ₀ =698,07*23/95+25024/95=432кН

Определяем требуемую площадь ветвей и назначаем сечение. Из условия устойчивости при центральном сжатии для подкрановой ветви:

А_в1= N_в1/ j R_yγ_с γ_с=1,0

значение коэффициента j можно принимать в пределах j = 0,7...0,9, тогда

А_в1= 423*10/(0,7*230*1) =26см²

По сортаменту (табл. 10 приложения) подбираем двутавр N 35Б1

А_в1= 48.7 см²; i_х= 3,35 см; i_у=14.3см.

Для наружной ветви:

А_в2=N_в2/ j R_yγ_с= 1357*10/(0,7*230*1)=84см²

Для удобства прикрепления элементов решетки расстояние между внутренними гранями полок принимаем таким же, как в подкрановой ветви

h _w’=h–2t=346.6-2*8.8 = 329мм,

где соответственно высота сечения подкрановой ветви и толщина ее полки.

Толщину стенки швеллера для удобства соединения ее вcтык c полкой подкрановой части колонны, принимаем равной t _w = 1,2 мм, т.е. одинаковый c толщиной полки надкрановой части. А высоту стенки швеллера назначаем с учетом толщины полок и сварных швов h _w =360 мм.

Требуемая площадь полок

А_f= (А_т2(в2)- t _w h _w)/2= (84– 1.2*36)/2 =20.4см²

Из условия местной устойчивости полки швеллера (при l= 0,8...4)

_{bf £(0,43+0,08`l) Ö E/Ry≈15}

_{bf = 15*tf; bf = tf*15tf =20.4 см2}

_{tf Ö20.4/15 =1.17см.}

_{принимаем tf = 1,2 см, bf =Аf/tf – 20.4/1,2 =17см,}

_{Принимаем bf =18см}

Геометрические характеристики ветви:

_Ав2= t _w h _w +2 _{bf tf =1,2*36+2*1,2*18=86см2}

z₀= (t _w h _w 0.5 t _w +2 _{bf tf} (0.5 b_f+ t_w) )/ А_в2=

=(1,2*36*0,5*1.2+2*1,2*18(0,5*18+1,2))/86=5.4см

I_X2 = (z₀-0.5 t _w)²+2 b_f t_f(0.5 z₂ -0.5 z₁) ²+ 2t_f b_f³ / 12

_где z₁₌ z₀ - t _w= 5.4-1.2=4.2 см

_z2 = _{bf -z1 = 18-4.2 =13.8 см}

I _X2 = 1.2*36*(2-0.5*1.2)²+2*18*1,2х(0,5*13.8-0,5*4.2)²+ 2+1,2*18³/12= 2430см ⁴

I _у =t _wh _w³ /12+2t_f b_f((h _w’ + t _w)/2)²=

=1.2*36³/12 + 2*1,2*18*((32.9+1,2)/2)²=17224см ⁴

i_х2=_ÖI_X2/А_в2=_{Ö2430/86=5.32 см;}

_iу=_ÖI_у/А_в2=_{Ö17224/86 = 14.15 см.}

Уточняем положение центра тяжести сечения колонны:

h₀=h_H-z₀=100-5.4=94.6см

_у1=А_в2/₍А_в1+А_в2)h₀=86/(48.7+86)*94.6=60.4см

у₂=h₀-у₁= 94.6-60.4=34.2см.

Отличие от первоначально принятых размеров велико, поэтому усилия в ветвях пересчитываем:

Усилие в наружной ветви

N_в2=|N₂|у₁/h ₀+M₂/h ₀ =684,42*60,4/94,6 +79673/94,6=1279кН

Усилие в подкрановой ветви

N_в1=|N₁|у₂/h ₀+M₁/h ₀ =698,07*34,2/94,6+25024/94,6=517кН

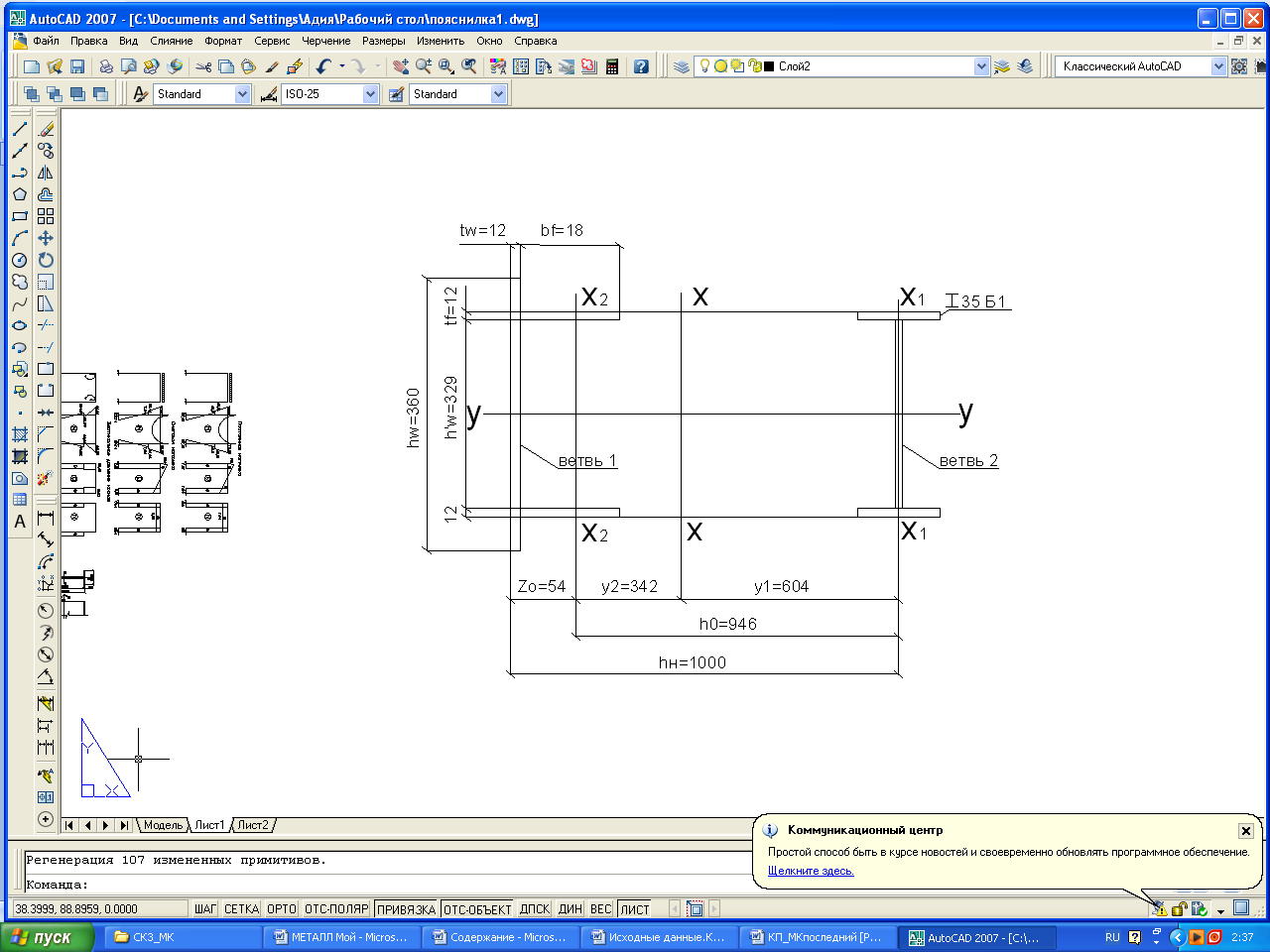
Рис.9 Сечение нижней (подкрановой) части колонны

Проверка устойчивости ветвей колонны из плоскости рамы

(относительно оси у-у)

l_efy^н = 1020 см.

Подкрановая ветвь:

l_y= l_efy^н/i_y= 1020/14.3=71

Из таблицы 9 приложения находим при R_y=230 МПа и l_y=71 j_у =0,755

σ=N_в1/ j_у А_в1=517*10/0,755*748,7=141 МПа < R_y=230 МПа

Наружная ветвь:

l_y= l_efy^н/i_y= 1020/14,15=72

Из таблицы 9 приложения находим при R_y=230 МПа и l_y=72 j_у =0,748

σ=N_в2/ j_у А_в2=1279*10/0,748*86=192МПа < R_y=230 МПа

Из условия равноустойчивости подкрановой ветви в плоскости и из плоскости рамы определяем требуемое расстояние между узлами решетки

l_х1= ℓ_в1/i_х1 = l_y=71

ℓ_в1^(тр) 71 i_х1 =71*3,35=238 cм

Разделив нижнюю часть колонны на целое число панелей

примем l_в1 < l_в1^тр

ℓ_в1= (Н_н- h_тр-10)/5=(1020-80-10)/5 =186см < 238 cм

Проверка устойчивости ветвей колонны в плоскости рамы

(относительно осей х₁-х₁ и х₂ – х₂).

Для подкрановой ветви:

l_х1= ℓ_в1/i_х1 =186/3,35=54

По таблице 9 приложения j_х1 =0,829

б=N_в1/ j_х1 А_в1= 517*10/0,829*48.7=128МПа < R_y=230 МПа

Для наружной ветви

l_х2= ℓ_в1/i_х2 =186/5,32=35 j_х2=0,915

б=N_в2/ j_х2 А_в2= 1279*10/0,915*86=163 МПа < R_y=230МПа

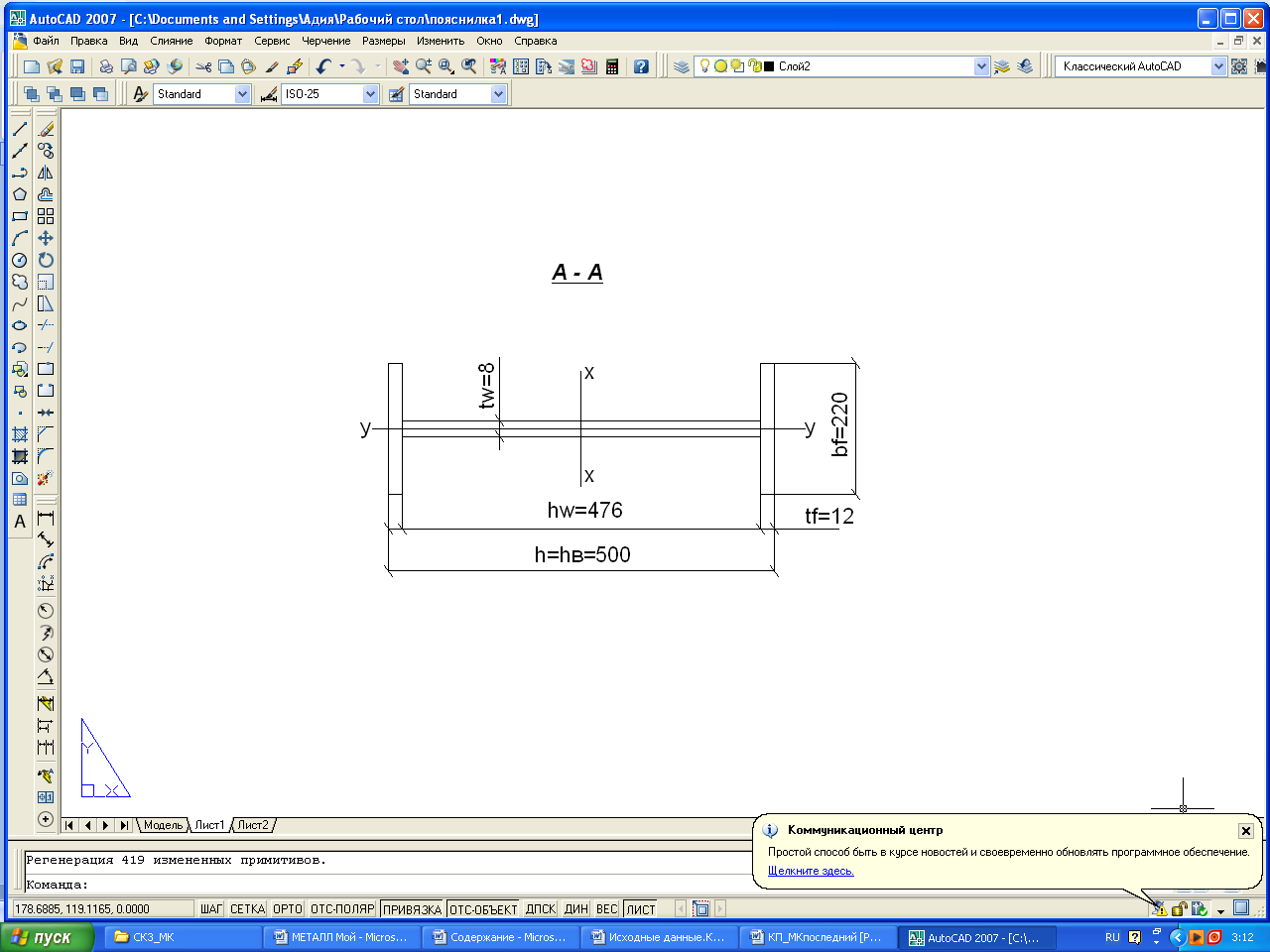
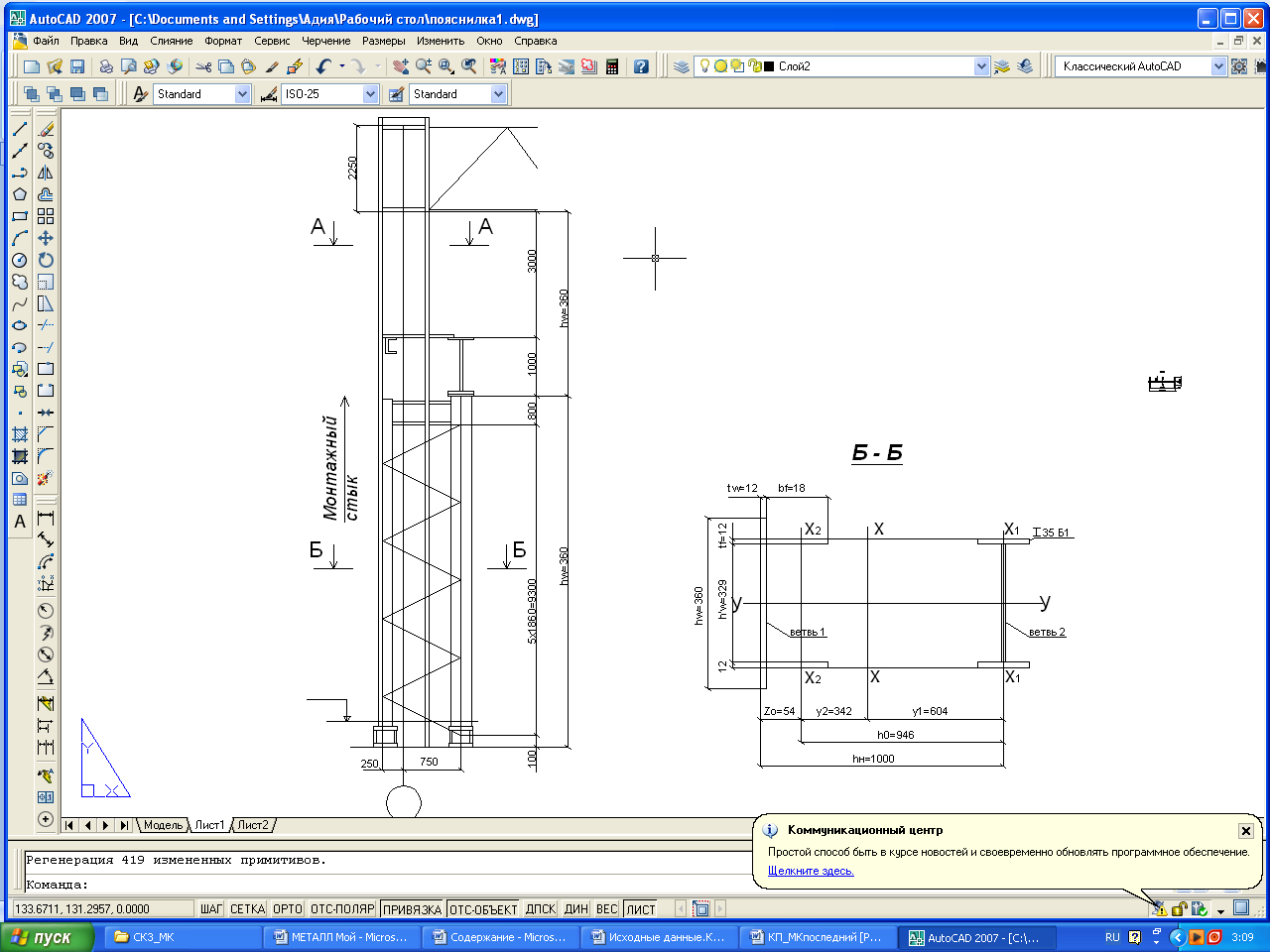
Рис.10

Расчет решетки подкрановой части колонны

Поперечная сила в сечении 4-4 колонны Q_mах=131,12кН (нагрузки 1,2,3.4(-Q),5*)

Условная поперечная сила

Q_fic=7,15*10^-6(2330- E/R_y) N/j,

где А = А_в1+А_в2=48,7+86=134,7см²

В соответствии с таблицей 8,2 R_y=230 МПа

Q_fic= 0.24 A = 0.24*134,7=32 кН < Q_mах=131,12кН

Расчет решетки производим на действие силы Q_mах

Усилие сжатия в раскосе N_р

N_р= Q_mах/ (2sinα)

Sinα= h_H/ℓ_p= h_H/_Ö h_H²+ (ℓ_в1/2)²= 100/Ö100²+(186/2)²=0,74

N_р=131,12/2*0,74=89 кН

Принимаем гибкость раскоса равной l_р= 100, тогда j=0,56

Для раскоса из одиночного уголка требуемая площадь

А_р.тр = N_р /j R_yγ_с=89*10/(0,56*230*0,75)=9,2см²

Для сжатого уголка, прикрепляемого одной полкой γ_с = 0,75.

По сортаменту [1, приложение 14, таблица 3] принимаем уголок 80х6

А_р=9,38 см²; i_min =i_y=1,58cм

l_max= ℓ_p/i_max=136,6/1,58 =86;тогда j=0,654

Напряжение в раскосе

σ=N_p/ jА=89*10/0,654*9,38=145МПа< R_yγ_с=230*0,75=172 MПа

Геометрические характеристики всего сечения:

А = А_в1+А_в2=134,7см²

I_x=А_в1y₁²+А_в2y₂²=48,7*60,4 ²+86*34,2²= 278254cм ⁴

i_x=_ÖI_x/ А=_Ö278254/134,7=45,5см.

l_x= l_efх^н/i_х=2040/45,5=45

Приведенная гибкость

l_ef=_Öl_x² + α₁ А/А_{р1 ,}

где α₁ коэффициент, зависящий от угла наклона раскосов,

при α = 45...60⁰ можно принять α₁ – 27

А_р1 - площадь сечения раскосов по двум граням сечения колонны

А_р1=2 А_р=2 *9,38 = 18,76 см²

l_ef=_Ö45²+27*134,7/18,76=47

Приведенная условная гибкость

`l_ef=l_{ef Ö Ry/ E=47Ö230/206000=1,56}

Проверка на комбинации усилий в сечении 4-4, догружающих наружную ветвь:

М₂=798,73 кН м, N₂=-684,42кН, у₂=34,2см, Z₀=5,4см

М₂A/|N₂|I_x(у₂+z₀)= 79873*134,7/684,42*278254*(34,2+5,4)=2,24см

По таблице 11 приложения определим j_е= 0,290

σ=N₂/ j_е А=684,42*10/0,290*134,7=175МПа<R_y=230 МПа

Проверка на комбинацию 3-3 усилий в сечении 3-3,: догружавших подкрановую ветвь:

М₁=-250,24 кН м ; N₁=-698,07 кН

m = М₁A/N₁I_xу₂= [25024*134,7/(698,07*278254)]*60,4=1

j_e =0,45

σ=N₁/ j_еА=698,07*10/(0,45*134,7)=115МПа<R_y=230 МПа

Устойчивость сквозной колонны как единого стержня из плоскости действия момента проверять не нужно, так как она обеспечена проверкой устойчивости отдельных ветвей.

Расчет и конструирование узла сопряжения верхней и нижней части колонны

Расчетные комбинации усилий в сечении 2-2 над уступом:

1)+ M_max= +84,37 кНм; N_соотв=108кН;

2) -M_max= -64,25кНм; N_соотв=158,4кН;

Давление кранов D_mах =590,07кН.

Прочность стыкового шва (w₁) проверяем по нормальным напряжениям в крайних точках сечения надкрановой части колонны. Площадь шва равна площади сечения колонны.

Первая комбинация усилий M и N:

здесь R_wy=R_y

внутренняя полка

Вторая комбинация усилий M и N:

наружная полка

внутренняя полка

толщину стенки траверсы определяем из условия смятия

s=D_max/(l_ef*t_wtp) R_pγ_c

где ℓ_ef=b_o.p+2t_пл – длина сминаемой поверхности;

t_пл – толщина плиты, которую принимаем t_пл =2см,

b_o.p – ширина одного ребра подкрановой балки, b_op=30см

t_wтр – толщина стенки траверсы;

R_p – расчётное сопротивление стали снятию торцевой поверхности

R_p=R_un/ _m=360/1,025=350Мпа

L_ef=b_op+2*t_пл=30+2*2=34см

t_wtr D_max/(l_ef*R_p*γ_c)=590.07/(34*35*1)=0,5см

Принимаем t_wтр=0.8см

Усилия во внутренней полке верхней части колонны (вторая комбинация)

Длина шва крепления вертикального ребра траверсы к стенке траверса (W2) при приварке четырьмя швами

применяем полуавтоматическую сварку проволокой марки Cв-08А, d=1,4….2мм.

Из таблицы 12 приложения находим β_f=0,9 β_z=1.05

назначаем k_f=6мм,

R_wz=0.45*R_un=0.45*360=162Мпа=16,2кН/см²

По таблице 13 приложения

R_wf=180Мпа=18кН/см²

β_fR_wfγ_wf=0.9*18=16.2 кН/см²< β_zR_wzγ_wz=1.05*16.2=17 кН/см²

l_w2<85β_fk_f=85*0.9*0.4=30,6см

В стенке подкрановой ветви делаем прорезь, в которую заводим стенку траверсы.

Для расчета шва крепления траверсы к подкрановой ветви (w3) составляем комбинацию усилий, дающую наибольшую реакцию траверсы. Такой комбинацией будет являться сочетание 1,2,3*,4(-), 5,

N=153,36кН, М=-20,986кНм

F=N h_в/2h_H-М/ h_H+0,9 D_mах=153,36*50/(2*100) - (-2098,6)/100 + 0,9*

*590,07=590,39кН,

здесь коэффициент "0,9" учитывает, что усилия N и М приняты для второго основного сочетания нагрузок.

Требуемая длина шва

l_w3^треб= F/(4β_f k_f R_wf γ_wf =)=590,39/(4*0,4*16,2) = 23cм

l_w3^треб<85β_f k_f=85*0,9*0,4 =30,6см,

Из условия прочности срезу стенки подкрановой ветви, в месте крепления траверсы, определяем высоту траверсы

h_тр≥F/2t_wв R_s γ_c=590,39/2*0.6*13*1=38cм,

где t_wв=0,6 толщина стенки подкрановой ветви (35Б1);

R_s - расчетное сопротивление стали срезу;

R_s=0,58*R_yn/γ _m=0,58*235/1,025 = 130 МПа = 13 кН/см²

Принимаем h_тр=80см

Проверим прочность траверсы как балки, нагруженной усилиями М, N и D_mах (смотри рис. 4.5). Ширина нижнего пояса траверсы b_тр = h _w’-3мм=376-3=373 мм.

Ширина верхнего горизонтального ребра траверсы

b_р =(h_w’-t_wтр)/2-(20...30мм) = (329-8)/2-20=140мм.

Конструктивно принимаем нижний пояс траверсы из листа размерами 326х12мм, верхние горизонтальные ребра из двух листов 140х12мм.

Найдем геометрические характеристики траверсы

Положение центра тяжести сечения траверсы;

y_н=(2*14*1,2*64,4+0,8*78,8*40,6+1,2*32,6*0,6)/( 2*23*1,2+0,8*78,8+1,2*32,6)=30см.

I_x=0,8*78,8³/12 + 78,8*0,8*10,6²+1,2*32,6*29,4² +2*14*1,2*34,4²=

=113278см⁴.

W_min =I_x/ y_в= 113278/50=2266 cм³

y_в= h_тр – у_н=80-30=50 см.

Максимальный изгибающий момент в траверсе возникает при второй комбинации усилий:

M_тр=F_тр1(h_н–h_в)=[-М/h_н+h_в/(2 h_н)](h_н–h_в)=

=[6425/100+158,4*50/(2*100)]*(100 - 50) = 5193кН.cм

σ_тр=M_тр/W_min=5193 /2266=2,3кН / см <Ry=23 кН/cм²

Максимальная поперечная сила в траверсе (с учетом усилия от кранов) возникает при комбинации усилий 1,2,3*,4 (см. расчет шва 3):

Q_mах =Nh_в/(2h_н)-M/h_н +k D_mах0.9/2=153,36*50/(2*100)-(-2098,6)/100+

+1,2*590,07*0.9/2= 378 кH

Здесь коэффициент k=1,2 учитывает неравномерную передачу усилия D_mах

τ _тр = Q_mах /(t _wтр h _wтр )= 378/(0,8*78,8) =6кН/см² < Rs = 23 кН/см².

Расчет и конструирование базы колонны

Ширина нижней части донны больше одного метра, поэтому базу проектируем раздельного типа.

Исходные данные:

опорную плиту базы колон принимаем из стали С235, у и второй при толщине проката

20 < t< 40 мм расчетное сопротивление R_у = 220 МПа =22кН/см²;

Материал фундамента - бетон В7,5; расчетные комбинации усилий в нижнем сечении колонны (сечение 4-4, табл. 2.3);

а) для расчета базы подкрановой ветви принимаем комбинацию уси­лий N_mах, - М_соотв.

Здесь сне­говая нагрузка не учитывается, так как она разгружает подкрановую ветвь

N_mах1 = 684,42-45,36=639,06кН; - М₁ = -497,09+26,77= -470,32кН м;

б) для расчета базы наружной ветви принимаем комбинацию усилий

N_mах,+М_соотв

N_mах2 = 684,42кН; + М₂ = 796,73 кН м.

Определим усилия в ветвях колонны

N_в1=|N₁|y₂/h₀ +|M₁|/h₀ = 639,06*34,2/94,6 +47032/94,6 =728 кН;

N_в2=|N₂|y₁/h₀ +|M₂|/h₀ = 684,42*60,4/ 94,6+ 79673/94,6=1279 кН;

База наружной ветви

Рассчитывается как база центрально сжатой колонны.

Определим размеры опорной плиты. Требуемая площадь плиты

А_пл^тр = N_в2 / R_ф = 1279 / 0,54= 2369см²,

где R_ф =γ R_б = 1,2*0,45 = 0,54 кН/см², для бетона класса В 7,5

R_б = 0,45кН/см².

Талица.3

Класс бетона	В 7,5	В 10	В 12,5	В 15
Расчетное сопротивление бетона осевому сжатию, Rб МПа	4,5	6,0	7,5	8,5

По конструктивным соображениям свес плиты С₂ должен быть не менее 4 см. Тогда ширина плиты

В > b_K + 2C₂ =35,3 + 2* 4 =43,3 см,

где b_к = h_w^' + 2 t_f = 32,9 + 2*1.2=35,3 см

Принимаем В =50 см.

Требуемая длина плиты

L_треб = А_пл ^тр / В = 2369/50 = 47,38см,

Принимаем L =50 см.

А_пл = 50 х 50 = 2500см² > А_пл ^тр = 2369 см².

Среднее напряжение в бетоне под плитой базы

σ_ф = N_Β2 / А_пл = 1279 / 2500 = 0,51 кН/см²

По условиям симметричного расположения траверс относительно центра тяжести ветви, находим расстояние между траверсами в свету

ℓ = 2(b_f + t_w – z₀) = 2*(18 + 1,2 – 5,4) =27,6 см.

При толщине траверсы t_тр=1,2 см.

С₁ = (L - ℓ – 2t_тр) / 2 = (50 – 27,6 - 2 *1,2) / 2 = 10см

Для определения толщины плиты подсчитаем изгибающие моменты на отдельных ее участках (см.рис.4.6);

в защемлении консольного свеса плиты на участке 1

М₁=σ_ф С₁²/2=0,51*10²/2 =25,5кН см;

в защемлении консольного свеса плиты на участке 2

М₂=σ_фС₂²/2= 0,581*7²/2 = 12,5 кН см.

где С₂ = (В - b_к)/2 = (50 – 35,3)/2=7см.

Участок 3 – плита опертая на четыре канта при

b/а = h_w^'/ b_f = 32.9 /18 = 1.83

М₃ = α σ_ф а² = 0,1* 0,51*18² =16.52 кН см.

Коэффициент α для расчета на изгиб плит, опертых на четыре канта

Таблица.4

b/a	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2	>2
α	0.048	0.055	0.063	0.069	0.075	0.081	0.086	0.091	0.094	0.098	0.1	0.12

участок 4 - плита, опертая на четыре канта, при

b/a= h _w’/(l-b_f - t_wтр)= 32.9/(27.6-18– 1,2) =3.92>2

α = 0.125

М₄ = α σ_ф а² =0,125 *0,51*8.4² =4.5кН см.

Для расчета принимаем максимальное значение изгибающего момента

М_mах = М₁ =25.5 кН см;

Требуемая толщина плиты

t_пл^тр = √6 М_mах / R_y=√6*25.5/22=2.6 см

Принимаем t_пл =30мм.

Высоту траверсы определяем из условия размещения шва крепления траверсы к ветви колонны. Будем считать, что все усилие в ветви передается на траверсу через четыре угловых шва. Применяем полуавтоматическую сварку проволокой Св-08А α=1,4...2 мм, k_f=6мм.

Из условия сопротивления срезу

l_w=N_Β2/(4 k_f β_f R_wf γ_wf γ_c)=1279/(4 *0.6*0,9*18) =33см

l_w<85 β_f k_f =85*0,9*0,6= 61 см

Требуемая высота траверсы

h_тр ^трeб =l_w+1см=33 + 1=34см,

принимаем h_тр = 35см.

База подкрановой ветви рассчитывается на усилия, возникавшие в нижнем сечении этой ветви, в описанном выше порядке.

Анкерные болты

Рассмотрим анкерные болты, закрепляющие подкрановую ветвь.

Для расчета учитываем комбинации усилий двух типов в сечений 4-4

1)+ M_max= 766.67кНм; N _соотв. = - 323.42кН;

2)N _min= -108кН; +М _соотв. = 724.09 кН м.

Из условия равновесия по моментам определим усилие растяжения болтов

Z= (М - |N| а)/у;

Z₁= (766.67-323.42*0.342)/0.946 =694 кН;

Z₂= (724.09-108*0.342) / 0.946= 728 кН

Z_мах = Z₂=728кН;

Для болтов принимаем сталь Вст3кп2. Расчетное сопротивление растяжению анкерных болтов из этой стали

R_ва = 185 МПа =18,5 кН /см²

Требуемая площадь сечения анкерных болтов.

∑ A_bn = Z_мах/R_ва =728/18.5=40 cм²

Принимаем 2 болта диаметром 56мм по

A_bn = 2х20.5=41 см ²

Таблица 5

D, mm	30	36	42	48	56	64	72	80	90	100
Abn см 2	5.6	8.2	11.2	14.7	20.5	26.9	34.7	43.5	56.0	72.0