2.2.2. Обратное преобразование Лапласа

Обратное преобразование Лапласа позволяет перейти от изображений к оригиналам. Из теории функции комплексного переменного известно, что если функция F(p) аналитична и интегрируема в пределах от c - j до c + j, то существует интеграл

f(t) = (1/2j) ^.  F(p) ^. e^pt dp. (2.7)

Эта формула, носящая название обратного преобразования Лапласа, представляет собой решение интегрального уравнения (2.6) относительно функции f(t). Переход F(p)  f(t) непосредственно по формуле (2.7) не всегда удобен из-за сложности, поэтому на практике используют различные приближенные методы оценки вида функции f(t). При анализе сложных электрических цепей чаще всего применяют теорему о вычетах (теорему разложения), которая позволяет представить подынтегральное выражение в (2.7) в виде суммы ряда простых слагаемых и заменить операцию интегрирования операцией суммирования этих слагаемых. Другой путь реализации обратного преобразования Лапласа заключается в использовании специальных таблиц, связывающих оригиналы и изображения. Эти таблицы составлены для множества функций F(p) и f(t) и приводятся в справочной математической литературе, в учебниках по теоретическим основам электротехники, теории сигналов и цепей. В табл. 2.1 приведена выписка некоторых преобразований.

3. Типовые структуры электронных устройств и их свойства

3.1. Последовательная структура и ее свойства

При последовательном соединении (рис. 3.1а) блоков входной сигнал X системы умножается на коэффициент передачи К1 первого блока. Выходной сигнал X1 первого блока умножается на коэффициент передачи К2 второго блока и таким образом формируется выходной сигнал Y всей системы. В общем случае коэффициенты передачи К1 и К2 являются комплексными величинами и их можно представить в показательной форме: К1 = k₁[exp(j₁)] и К2 = k₂[exp(j₂)]. С учетом этого уравнение преобразования для последовательной структуры можно записать в виде

Y = KX = k₁k₂[exp(j(₁+₂))]X = k[exp(j)] X.

Из полученного уравнения следует, что при последовательном соединении блоков: 1) k = k₁k₂ – общий коэффициент передачи равен произведению коэффициентов передачи отдельных блоков; 2)  = ₁+₂ – общий сдвиг фаз равен сумме сдвигов фаз отдельных блоков.

Используя первое свойство, проанализируем погрешность коэффициента передачи системы при последовательном соединении блоков. Обозначим символами ₁ и ₂ погрешности коэффициентов передачи первого и второго блоков соответственно. Прологарифмируем и продифференцируем формулу для общего коэффициента передачи, чтобы перейти от величин k, k₁, k₂ к их относительным приращениям , ₁, ₂. В результате имеем

k = k₁k₂; lnk = lnk₁+lnk₂; (k/k) = (k₁/k₁) + (k₂/k₂);  = ₁ + ₂.

Таким образом, относительная погрешность общего коэффициента передачи равна сумме относительных погрешностей коэффициентов передачи отдельных блоков. Эта погрешность является мультипликативной по характеру, т.к. ее относительное значение не зависит от входной величины X.

Чтобы получить формулу для расчета погрешности смещения нуля, предположим, что каждый блок имеет собственную погрешность смещения нуля: X₀₁, X₀₂. Обычно наличие данной погрешности отображается на структурной схеме блока введением на входе идеального сумматора. На один вход сумматора подается основной сигнал, а на другой – сигнал, соответствующий смещению нуля данного блока. При этом считается, что блок уже не содержит никаких погрешностей и осуществляет преобразование сигналов с номинальным коэффициентом передачи (рис. 3.1г). Уравнение преобразования, учитывающее наличие погрешностей X₀₁, X₀₂, в этом случае принимает вид Y_p = ((X + X₀₁) k₁+X₀₂) k₂ = k₁k₂  X+Y₀.

Вэтом уравнении первое слагаемое определяет полезный сигналY, а второе – погрешность, приведенную к выходу системы Y₀ = k₁k₂^.X₀₁+k₂X₀₂. Погрешность Y₀ носит аддитивный характер, т.к. ее абсолютное значение не зависит от входной величины X.

Рис. 3.1. Типовые структурные схемы: а) последовательная; б) параллельная; в) встречно-параллельная; г) эквивалентная схема,

учитывающая наличие у блока смещения нуля Х₀

В схемотехнике аддитивные погрешности принято оценивать, предварительно приведя их ко входу блока или системы. С этой целью необходимо значение погрешности, приведенное к выходу Y₀, разделить на общий коэффициент передачи K = k₁k₂. В результате имеем X₀ = Y₀/K = X₀₁ + X₀₂/k₁.

Таким образом, при последовательном соединении блоков системы общая аддитивная погрешность практически полностью определяется аддитивной погрешностью первого блока. Влияние же аддитивных погрешностей последующих блоков уменьшается пропорционально общему коэффициенту передачи предыдущих блоков.

Чтобы решить вопрос о форме амплитудно-частотной характеристики (АЧХ) последовательного соединения, необходимо задать форму АЧХ первого и второго блоков. Для простоты предположим, что блоки являются апериодическими звеньями первого порядка. При этом возможны следующие сочетания АЧХ:

1. оба блока имеют АЧХ интегрирующего типа, когда

K1(p) = k₁/(1+p₁) и K2(p) = k₂/(1+p₂);

2. оба блока имеют АЧХ дифференцирующего типа, когда

K1(p)=k₁^. p₁/(1+p₁) и K2(p) = k₂ ^. p₂/(1+p₂);

3) один блок имеет АЧХ интегрирующего типа, а другой – дифференцирующего, когда

K1(p) = k₁/(1+p₁) и K2(p) = k₂^p₂/(1+p₂).

В формулах для передаточных функций использованы обозначения: р = j – оператор Лапласа; ₁, k₁ и ₂, k₂ – постоянные времени и коэффициенты передачи первого и второго блоков соответственно.

Поскольку при последовательном соединении передаточные функции перемножаются, то нетрудно получить следующие выражения для передаточной функции последовательного соединения:

1) K(p) = k₁k₂/[(1+p²₁₂)+p(₁+₂)];

2) K(p) = k₁k₂ ^. p²₁₂/[(1+ p²₁₂)+p(₁+₂)];

3) K(p) = k₁k₂ ^. p₂/[(1+ p²₁₂)+p(₁+₂)].

Чтобы перейти к АЧХ, необходимо заменить в К(р) оператор р на j, полученное комплексное выражение привести к стандартному виду, выделив действительную и мнимую части, и найти модуль комплексного выражения.

Р

Основные выводы из этого анализа заключаются в следующем.

Для 1-го и 2-го вариантов форма АЧХ остается апериодической (монотонно убывающей или монотонно возрастающей) с частотой среза, определяемой наименьшей из двух частот:

f₁ = 1/2₁ или f₂ = 1/2₂.

Крутизна результирующей АЧХ возрастает в два раза по сравнению с крутизной АЧХ одного блока.

Для 3-го варианта форма результирующей АЧХ становится резонансной с максимумом

(макс К) = k₁k₂/(1+f₂/f₁)

на частоте f = (f₁f₂)^0,5.

езультаты качественного анализа АЧХ К() для всех трех сочетаний представлены на рис. 3.2.

относительная частота f = (f₁f₂)^0,5

1

2

3

Рис. 3.2. АЧХ двух последовательно соединенных апериодических звеньев

(k₁ = 5, ₁ = 0,001 с, k₂ = 10, ₂=0,01 с): 1 – интегрирующего, 2 – дифференцирующего, 3 – смешанного типов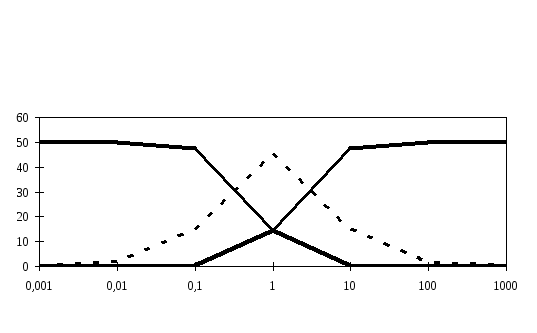

Таким образом, при последовательном соединении блоков:

1. коэффициенты передачи перемножаются;

2. фазовые сдвиги суммируются;

3. относительные погрешности коэффициента передачи суммируются;

4. аддитивная погрешность определяется погрешностью смещения и дрейфа нуля первого блока;

5. форма амплитудно-частотной характеристики зависит от формы АЧХ отдельных блоков и их сочетания.