7.1.5. Применение операционных усилителей

Преобразователи сопротивления в напряжение (ПСН) используются для согласования цепей с резистивными датчиками различных физических величин. Основными требованиями к ПСН являются: 1) обеспечение линейной и стабильной функции преобразования измеряемой физической величины через сопротивление датчика в выходное напряжение; 2) исключение влияния линии, соединяющей датчик, обычно расположенный на объекте измерения, со входом системы регулирования; 3) получение малого выходного сопротивления ПСН, при котором обеспечивается его удобное согласование со входом аналого-цифрового преобразователя. В литературе по операционным усилителям описано много вариантов построения ПСН, ориентированных на различные условия применения.

На рис. 7.3б представлена типовая схема ПСН, используемая для подключения датчиков температуры – термометров сопротивления, имеющих характеристику вида R_t = R₀  (1 + T), где R₀ – сопротивление датчика при начальной температуре, когда T = 0,  – температурный коэффициент сопротивления, определяющий чувствительность датчика, T – изменение измеряемой температуры относительно начальной.

Термометр сопротивления соединен с остальной цепью ПСН четырехпроводной линией с сопротивлениями r₁-r₄. Порядок величины сопротивлений линии связи совпадает с сопротивлением датчика, составляющим примерно 50 Ом. Измерительная цепь ПСН построена так, чтобы уменьшить влияние линии на результат измерения температуры.

Рис. 7.3

С помощью ОУ А2 на нижнем конце резистора R_t поддерживается нулевой потенциал, независимо от падения напряжения на линии r₂. Влияние линий r₃, r₄ исключается за счет того, что они включены последовательно с очень большими входными сопротивлениями ОУ А1 и А2 соответственно. Чтобы линия r₁ не оказывала существенного влияния, необходимо сопротивление R выбирать из условия R >> r₁. ОУ А1 выполняет две функции: во-первых, совместно с резистором R и стабилитроном V он задает ток I₀ = U₀/R для питания датчика и, во-вторых, с его помощью падение напряжения на датчике передается на выход ПСН. Уравнение преобразования ПСН имеет вид Uвых = U₀R_t/R, где U₀ – напряжение стабилизации стабилитрона. В соответствие с этим уравнением точность преобразования зависит от точности задания и стабильности параметров U₀ и R.

Преобразователи емкости в напряжение (ПЕН) используются для преобразования сигналов с емкостных датчиков физических величин. Принцип действия емкостных датчиков основан на том, что под воздействием измеряемой величины Х могут изменяться следующие параметры датчика: (Х) – относительная диэлектрическая проницаемость, А(Х) – площадь перекрытия пластин или d(X) – расстояние между пластинами. Емкость Cx = ₀(Х)^.А(Х)/d(X) датчика прямо пропорциональна (Х) и А(Х) и обратно пропорциональна d(X). Здесь символом ₀ обозначена электрическая постоянная.

На рис. 7.3в изображена типовая схема ПЕН. В зависимости от того, какой из параметров датчика изменяется под воздействием входной величины, датчик включается либо на входе ОУ – для (Х) и А(Х), либо в цепи обратной связи – для d(X). Тем самым обеспечивается линейная функция преобразования относительно величины Х. Поскольку данная схема представляет типовое инвертирующее включение ОУ А, то уравнение преобразования в операторной форме имеет вид

Uвых(р) = - Uвх(р)^. Z₂(р)/Z₁(p),

где Z₂(р) = 1/pC₀, Z₁(p) = 1/pCх. После подстановки получаем

Uвых(р) = - Uвх(р) ^. Сх/C₀.

Таким образом, коэффициент передачи ПЕН прямо пропорционален емкости Сх датчика. Т-образная цепь, состоящая из двух резисторов сопротивлением R и конденсатора емкостью Сф, необходима для создания связи по постоянному току инвертирующего входа и выхода ОУ. Тем самым обеспечивается правильный режим работы ОУ. На функцию преобразования Т-образная цепь при достаточно больших значениях R (порядка единиц МОм) влияния не оказывает. Точность преобразования определяется точностью задания и стабильностью амплитуды входного сигнала и емкости обратной связи С₀.

Компенсационный стабилизатор напряжения (КСН) используется для получения высокостабильных уровней напряжения, необходимых для питания различных электронных блоков и устройств. Понятие стабильности включает в данном случае такое свойство КСН, при котором его выходное напряжение почти не зависит от колебаний напряжения питающей сети и изменений сопротивления нагрузки КСН.

Основными параметрами КСН являются:

1) коэффициент стабилизации, который показывает, во сколько раз относительная нестабильность Uвх/Uвх напряжения на входе стабилизатора больше относительной нестабильности Uвых/Uвых напряжения на выходе:

Кст = (Uвх/Uвх)/(Uвых/Uвых);

2) выходное сопротивление, которое показывает, на сколько вольт изменяется выходное напряжение КСН при изменении выходного тока на 1 А:

Rвых = Uвых/Iвых;

3) температурный коэффициент выходного напряжения, который показывает, на сколько процентов изменяется выходное напряжение КСН при изменении температуры среды на 1^оС:

ТКвых = (Uвых/Uвых)/T.

Чем больше Кст и меньше Rвых и ТКвых, тем выше качество стабилизатора. Если в параметрических стабилизаторах Кст  5-50, Rвых  (5–20) Ом, то в КСН, построенных на базе ОУ, несложно получить Кст  500-5000, Rвых составляет сотые доли ом при выходных токах от 1 мА до 10 А. На рис. 7.3г показана схема простейшего КСН, основой которого является неинвертирующий усилитель постоянного тока на ОУ. Входным сигналом этого усилителя служит напряжение U₀, снимаемое со стабилитрона V. Транзистор VT используется для увеличения выходного тока ОУ. Цепь ООС замыкается через делитель напряжения R1, R2. Для увеличения стабильности опорного напряжения U₀ параметрический стабилизатор, состоящий из стабилитрона V и резистора R3, подключен к выходному напряжению стабилизатора. Цепь питания самого ОУ подключена к однополярному источнику нестабилизированного входного напряжения Uвх. Формулу для выходного напряжения можно получить, если приравнять напряжения, действующие на НЕ- и И- входах ОУ: U₀ = Uвых  R1/(R1 + R2), откуда Uвых = U₀ (1 + R2/R1). Изменяя соотношение между сопротивлениями резистивного делителя, можно регулировать выходное напряжение в диапазоне от U₀ до (Uвх – 3В).

О

Рис. 7.4

перационные преобразователи (ОП) – это преобразователи, предназначенные для выполнения математических операций над аналоговыми сигналами. Основой построения ОП является ОУ, который для получения требуемой функциональной зависимости охватывается либо линейной, либо нелинейной, либо инерционной обратной связью.

Суммирующий усилитель (СУ) представлен на рис. 7.4а. Его базой является инвертирующее включение ОУ. Уравнение преобразования СУ имеет вид

Uвых = – R(Ui/Ri),

где i – переменная суммирования, максимальное значение k которой определяет количество слагаемых. Суммирование осуществляется с учетом знаков входных сигналов, т.е. алгебраически, и весов слагаемых, что определяет функциональную гибкость подобного СУ. Важнейшим достоинством СУ является то, что источники входных сигналов между собой развязаны нулевым потенциалом инвертирующего входа. В свою очередь, отсутствие связи между источниками увеличивает точность реализации операции суммирования.

Рис. 7.4

Расчет суммирующего сопротивления R ведется из условия, что при максимальных значениях входных напряжений суммарный входной ток не будет превышать предельного выходного тока ОУ, а выходное напряжение при этом будет меньше напряжения насыщения ОУ.

Таким образом:

R = Uнас/Imax = 0,8E/Imax,

где Е – напряжение питания ОУ; Imax – предельный выходной ток ОУ. В соответствии с уравнением преобразования, точность СУ в первую очередь определяется точностью и стабильностью его резисторов. Поэтому надо использовать либо объемные прецизионные резисторы, либо гибридные микросборки наборов резисторов, изготовленных с использованием лазерной подгонки.

Интегратор. Простейший интегратор строится так, как показано на рис. 7.4б. Этот интегратор имеет передаточную функцию вида

K(p) = –1/(pRC),

которая говорит о том, что выходное напряжение равно интегралу по времени от входного напряжения, взятого с обратным знаком, причем постоянная времени интегрирования  = RC. Однако если учесть неидеальность ОУ, проявляющуюся в том, что К₀  , то передаточная функция принимает вид передаточной функции апериодического звена первого порядка интегрирующего типа с коэффициентом передачи К₀ и постоянной времени 0 = К₀, т.е. K(p) = – К₀/(1 + pК₀).

Таким образом, имеем погрешность линейности

_л1  t/(К₀),

где t – время интегрирования;  = RC – постоянная времени интегратора.

Отсюда можно сформулировать требование к собственному коэффициенту усиления ОУ в виде К₀ >> t/(_л1).

Зависимость коэффициента К₀ от частоты также приводит к появлению погрешности линейности

_л2  fсрUm/V,

где fср = 1/(2RC) – частота среза RC-цепи; Um – размах напряжения на выходе интегратора; V – скорость нарастания выходного напряжения ОУ.

Тогда суммарную погрешность линейности можно записать так:

_л  _л1 + _л1.

Статические неидеальности ОУ также приводят к появлению погрешностей. Так, наличие ЭДС смещения нуля и его дрейф приводят к появлению на выходе интегратора сигнала, возрастающего во времени:

Uвых₀(t) = e₀(t)  (1 + t/),

а наличие входных токов – сигнала:

Uвых_I(t) = I_ (t/C).

Анализ погрешностей схем на основе интегратора, вызванных наличием последних двух факторов, должен проводиться применительно к конкретной схеме.

Логарифмирующий преобразователь (ЛП). Принцип действия ЛП удобно пояснить на простом примере (рис. 7.4в). Если во встречно-параллельной структуре в цепи обратной связи использовать нелинейный элемент, то структура в целом будет реализовывать функцию, обратную нелинейности элемента обратной связи. Поэтому, чтобы получить логарифмическую зависимость выходного напряжения от входного, в цепи обратной связи ОУ использован диод, имеющий, как известно, экспоненциальную ВАХ вида

I_v = I₀(exp(U/_t) – 1).

Исходя из принципов расчета схем с ОУ, ток через диод V определяется входным током I_v = Uвх/R, а напряжение на диоде равно выходному напряжению ЛП: Uвых = U. При подстановке данных условий в уравнение диода, получим

Uвых = _t ln[Uвх/(RI₀) – 1].

Здесь _t = k T/q – температурный потенциал (примерно 26 мВ при комнатной температуре); k – постоянная Больцмана (1,38^.10^-23 Дж/K); q – заряд электрона (1,6^. 10^-19 Кл); Т – абсолютная температура; I₀ – обратный ток диода, имеющий для кремниевых диодов значение порядка 0,1 нА и зависящий от температуры (этот ток удваивается при увеличении температуры на каждые 10 ^оС).

Из анализа уравнения преобразования ЛП следует, что правильная работа схемы возможна лишь при условии введения специальных мер по температурной коррекции изменений параметров _t и I₀ диода. Обычно для этой цели применяют дифференциальное включение одинаковых р-n–переходов, в одном из которых ток определяется входным сигналом, а в другом поддерживается постоянным. В таких ЛП удается реализовать диапазон логарифмирования от 4 до 9 декад с погрешностью не более (1–5) %.

Выпрямители – это электронные устройства, предназначенные для преобразования переменного напряжения в постоянное. По назначению выпрямители можно разделить на следующие группы: 1) выпрямители среднего значения; 2) амплитудные выпрямители; 3) фазочувствительные выпрямители; 4) выпрямители эффективных значений.

Выпрямители среднего значения дают на выходе напряжение, постоянная составляющая которого пропорциональна среднему значению выпрямленного входного напряжения. Работа подобных выпрямителей, как правило, основывается на том, что при одной полярности входное напряжение с некоторым масштабным коэффициентом подается на выход, а при другой – выходное напряжение поддерживается равным нулю (однополупериодный выпрямитель) или инвертированному входному напряжению (двухполупериодный выпрямитель).

В последнем случае, если обеспечено равенство масштабных коэффициентов для прямого и инвертированного входных сигналов, то устройство может применяться также в качестве формирователя модуля входного сигнала: выходное напряжение оказывается пропорциональным абсолютному значению входного. Использование ОУ в точных выпрямителях преследует цель уменьшить погрешности преобразования, обусловленные неидеальными ВАХ диодов.

В качестве примера на рис. 7.4г представлена схема двухполупериодного выпрямителя среднего значения. Достоинством данного выпрямителя является малое количество используемых элементов, причем точными должны быть два резистора R1 и R2. ОУ А2 и диод V образуют аналоговый ключ, который может находиться либо в разомкнутом, либо в замкнутом состоянии в зависимости от полярности входного напряжения.

При положительной полярности Uвх(t) диод закрыт, ключ разомкнут и в цепи резистора R3 ток не протекает. В этом случае Uвх(t) приложено к НЕ- и соответственно к И-входу ОУ. Согласно принципам расчета схем с ОУ, токи через резисторы R1 и R2 в данном случае будут равны нулю и выходное напряжение

Uвых(t) = Uвх(t).

При отрицательной полярности Uвх(t) диод открыт, ключ замкнут и в цепи резистора R3 протекает ток открытого диода. Через диод замыкается цепь обратной связи с выхода ОУ А2 на его инвертирующий вход, в результате чего потенциал инвертирующего входа ОУ А2 и соответственно потенциал неинвертирующего входа ОУ А1 поддерживаются равными нулю. В этом случае ОУ А1, резисторы R1 и R2 образуют инвертирующий усилитель с коэффициентом передачи (R2/R1) = 1, так что на выходе ОУ А2 получается сигнал положительной полярности

Uвых(t) = – [– Uвх(t)].

На рис. 7.4д представлены временные диаграммы работы данного выпрямителя. Для источника входного сигнала рассмотренный двухполупериодный выпрямитель представляет переменное сопротивление, что является недостатком схемы.

Генераторы синусоидальных колебаний. Если требуется получить синусоидальное переменное напряжение низких или средних частот, то удобнее всего применять RC-генераторы с мостом Вина, один из вариантов которых изображен на рис. 7.5а. Генератор содержит неинвертирующий усилитель на ОУ и частотно-зависимую RC цепь.

Передаточная функция частотно-зависимой RC цепи имеет вид

W(p) = Uвых(p)/U₊(p) = p/(1 + 3p + p²²),

где  = RC. АЧХ этой цепи имеет максимум, равный 1/3 на частоте F₀ = 1/2RC, и нулевой фазовый сдвиг на этой частоте.

Таким образом, чтобы в системе выполнялось условие баланса амплитуд, необходимо иметь коэффициент усиления усилителя К = 3 или отношение R2 к R1, равное 2. Однако для возникновения колебаний нужно, чтобы вначале петлевое усиление было больше 1, а затем поддерживалось на уровне единицы. Выполнить данное требование и получить генератор гармонических колебаний с малыми искажениями формы можно, если применить нелинейную ООС.

В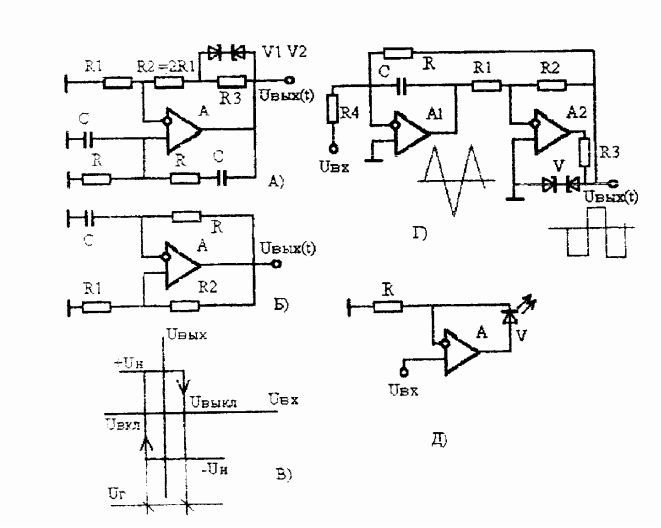схеме рис. 7.5а это достигается использованием резистора R3, шунтированного двухсторонним стабилитроном (или двумя одинаковыми стабилитронами, включенными встречно). Стабилизирующее действие данной нелинейной схемы заключается в следующем: при увеличении амплитуды выходного напряжения генератора выше некоторого порогового значения открывается стабилитрон и шунтирует сопротивление резистора R3.

Рис. 7.5

В результате коэффициент усиления неинвертирующего усилителя уменьшается со значения К = 1 + (R2 + R3)/R1 > 3 до значения К = 1 + (R2/R1) < 3. Уменьшение коэффициента усиления К ведет к уменьшению амплитуды сигнала на выходе. В реальных генераторах подобного типа удается получить уровень нелинейных искажений синусоидального сигнала (0,1–0,5) % при выходной амплитуде сигнала (5–10) В.

Если требуется обеспечить меньший уровень нелинейных искажений и получить высокую стабильность амплитуды автоколебаний, то цепь регулировки глубины ООС выполняют на основе сравнения амплитуды генерируемого напряжения с опорным постоянным напряжением.

Обычно вначале выпрямляют переменное напряжение с выхода генератора, затем из него вычитают опорное напряжение, а разность усиливают и используют для управления одним из сопротивлений, входящих в ветвь ООС генератора. В качестве управляемых сопротивлений чаще всего используют полевые транзисторы.

Генераторы прямоугольных импульсов. Наиболее простые из них строят, охватывая ОУ цепями ПОС и ООС, причем ПОС по своему действию во времени должна быть опережающей по отношению к ООС. Тогда цепь ПОС обеспечивает лавинообразный переход мультивибратора из одного состояния в другое, а цепь ООС (совместно с цепью ПОС) ограничивает время пребывания устройства в каждом из состояний. Генераторы прямоугольных импульсов часто называют мультивибраторами.

Схема мультивибратора, построенного на одном ОУ, представлена на рис. 7.5б. Цепь ПОС выполнена на основе резистивного делителя R1, R2, а цепь ООС содержит пассивный интегратор на элементах R, С. Часть генератора, которая содержит ОУ и цепь ПОС, называется триггером Шмитта. Амплитудная характеристика триггера Шмитта имеет гистерезисный характер. При симметричном напряжении питания ОУ уровни выходного напряжения насыщения одинаковы по модулю.

Напряжение на неинвертирующем входе, при котором ОУ переключается из одного состояния, соответствующего уровню +Uн, в другое состояние, соответствующее уровню –Uн, определяется выражением Uп = Uн  R1/(R1 + R2). Переключение ОУ происходит в те моменты времени, когда напряжение на конденсаторе С станет равным Uп. Зная закон изменения напряжения конденсатора С, соответствующий экспоненте, можно вывести формулу для периода колебаний мультивибратора: T = 2 RCln(1 + 2 R1/R2).

На рис. 7.5в показана амплитудная характеристика триггера Шмитта. На рис. 7.5г приведена схема мультивибратора, позволяющая получить на выходе интегратора (А1, С, R) напряжение треугольной формы с периодом Т = 4^. С^. R^.R1/R2 и амплитудой, равной UсR1/R2, где Uс – напряжение стабилизации двухстороннего стабилитрона V. На стабилитроне формируется выходное прямоугольное напряжение стабильной амплитуды Uс. Триггер Шмитта построен на ОУ А2, резисторах R1, R2, R3.

Подавая через дополнительный резистор внешнее напряжение на инвертирующий вход интегратора, можно регулировать скважность выходных прямоугольных импульсов (и среднее значение выходного напряжения) или симметрию треугольного сигнала.

Схемы мультивибраторов отличаются подходом к расчету. Расчет схем на базе пассивных интеграторов (подобных схеме рис. 7.5б) основан на применении законов коммутации и решении уравнений, представленных в экспоненциальной форме. А расчет схем на базе активных интеграторов (подобных схеме рис. 7.5г) базируется на использовании принципов расчета линейных электрических цепей.

Источники тока. Чтобы построить источник тока на базе ОУ, необходимо использовать ООС по току. Для этого, например, в инвертирующем включении вместо резистора R2 (рис. 7.1б) надо включить сопротивление нагрузки. Ток через это сопротивление будет определяться лишь входным напряжением и сопротивлением резистора R1: I = U₁/ R1. В теории цепей данная схема носит название источника тока, управляемого током (ИТУТ). Выходное сопротивление источника тока оценивается по формуле Rвых = К₀ ^. R1.

Для токов в диапазоне десятых долей – единиц миллиампер Rвых может достигать сотен мегаом. В качестве примера на рис. 7.5е представлена схема управления мощностью излучения светодиода или полупроводникового лазера. ОУ в неинвертирующем включении и резистор R образуют источник тока, управляемый напряжением (ИТУН), нагрузкой которого является светодиод. Интенсивность излучения светодиода линейно зависит от тока через светодиод: Ф = SI, где S – коэффициент преобразования, имеющий размерность напряжения и составляющий величину порядка 0,1 В. В свою очередь, ток через светодиод прямо пропорционален входному управляющему напряжению, т.е. I = Uвх/R, откуда имеем Ф = S^.Uвх/R. При указанном включении управляющее напряжение должно быть положительным.