В результате получаем

R1 = 2R2. (5.7)

Расчет R1 по формуле (5.7) дает приближенную оценку в силу наличия разброса значений  у БТ и сопротивлений резисторов. Поэтому в практических схемах последовательно с R1 вводится переменный резистор для более точной установки НРТ. Достоинством режима усиления класса А является малый уровень нелинейных искажений переменного сигнала. Основной недостаток связан с низкой экономичностью и малым (порядка 25 %) к.п.д. из-за того, что в отсутствие входного сигнала БТ потребляет от источника напряжения питания ток I_ка. В связи с этим обстоятельством режим усиления класса А применяют в каскадах предварительного усиления, в то время как в мощных выходных каскадах используются гораздо более экономичные режимы классов В и АВ.

5.1.4. Малосигнальные эквивалентные схемы и усилительные параметры бт

После того как установкой необходимого смещения в БТ задан режим линейного усиления, возникает проблема оценки усилительных параметров каскадов. К усилительным относятся следующие параметры: коэффициенты передачи по напряжению, току и мощности; входное и выходное сопротивления. Решение указанной проблемы основано на представлении самого БТ и всего усилительного каскада в виде линейного четырехполюсника – элемента с двумя входными и двумя выходными зажимами. Свойство линейности позволяет применять для расчета четырехполюсника известные методы анализа электрических цепей на переменном токе, например преобразование Лапласа.

При этом используется ряд допущений:

1. токи и напряжения в любой точке схемы состоят из постоянных (I или U) и переменных (dI или dU) составляющих, причем dI << I, dU << U;

2. связь между переменными составляющими dI и dU определяется через производные от функции I = f(U), а не самими этими функциями;

3. нелинейные элементы отображаются своими дифференциальными сопротивлениями.

Модель реальной цепи, в которой нелинейные элементы представляются линейными двух- или четырехполюсниками, в соответствии с принятыми допущениями, называется малосигнальной эквивалентной схемой (МЭС).

Для расчета усилительных параметров каскада на БТ необходимо:

1. составить МЭС самого БТ;

2. пририсовать к МЭС БТ внешние элементы, считая источники постоянного напряжения короткозамкнутыми цепями для сигналов переменного тока, а источники постоянного тока – разрывом;

3. максимально упростить полученную МЭС, используя конкретные условия задачи, рекомендации, физические соображения и т. д.;

4. по упрощенной МЭС вывести формулы для оценки усилительных параметров и подставить в них численные данные;

5. если упрощенная МЭС не дает требуемой точности анализа, ее следует дополнить, уточнить с учетом требований задания.

В частности, при составлении МЭС БТ используются следующие типовые упрощения:

1. не учитываются собственные емкости переходов и сопротивления пассивных слоев эмиттера, коллектора и базы;

2. дифференциальный и статический коэффициенты передачи тока базы принимают равными (d = ), а для коэффициента передачи тока эмиттера принимают d =  = 1;

3. коэффициенты передачи тока  и  от частоты не зависят;

4. эффект Эрли (изменение ширины базы при изменении напряжения на коллекторе) не учитывается.

Условимся обозначать переменные составляющие напряжений и токов на МЭС, в отличие от эквивалентных схем на постоянном токе, малыми буквами. Таким образом, "u" и "U" означают различные значения величины напряжения u = dU. Методика составления МЭС БТ проста: достаточно заменить переходы их дифференциальными сопротивлениями, а усилительные свойства БТ учесть введением источника тока, включаемого параллельно коллекторному дифференциальному сопротивлению.

На рис. 5.8 представлена МЭС БТ с ОБ. Рассчитаем собственные усилительные параметры БТ в схеме с ОБ.

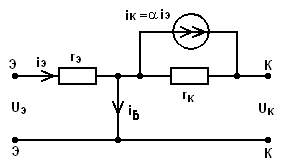
Рис. 5.8. Малосигнальная эквивалентная схема БТ в схеме с ОБ

Коэффициент передачи по току определяется по общей формуле K_i = i_вых/i_вх. Здесь входным является ток эмиттера, а выходным – ток коллектора, которые связаны между собой коэффициентом передачи   1. Поэтому K_i = i_к/i_э =   1.

Коэффициент передачи по напряжению K_u = u_вых /u_вх. Составим уравнение для u_вых = i_к r_к =  i_э r_к =  r_к u_вх/r_э.

В итоге получаем, что K_u = ^. r_к/ r_э  r_к/ r_э. Для численной оценки дифференциального сопротивления обратносмещенного коллекторного перехода используется формула Эрли

rк = U0/Iк, (5.8)

где U₀ – напряжение Эрли, составляющее (100–200) В для маломощных БТ; I_к – постоянная составляющая тока коллектора, рассчитываемая из условия заданного смещения, например по формуле (5.6) для режима класса А. В свою очередь, дифференциальное сопротивление прямосмещенного эмиттерного перехода рассчитывается из уравнения для ВАХ диода: r_э = _t/I_э. Подставив найденные значения r_к и r_э в формулу для K_u, получим

Ku = U0/_t = 100100/(2610^-3)  4^. 10⁵. (5.9)

Коэффициент передачи по мощности оценивается по формуле K_p = K_uK_i   K_u. Входное сопротивление R_вх = u_вх/i_вх представляет собой просто r_э = _t/I_э, оценка которого, например, для тока эмиттера 1 мА, дает r_э = 26 Ом.

Выходное сопротивление R_вых = u_вых/i_вых определяется только дифференциальным сопротивлением r_к = ^.U₀/I_к. Так, при I_к = 1 мА имеем значение r_к = 100 ^. 100/10^-3 = 10 МОм.

В табл. 5.3 представлены формулы для расчета усилительных параметров БТ в схемах с ОБ, ОЭ, ОК, а также численные оценки значений этих параметров.

Таблица 5.3

Включение/ параметры	ОБ	ОЭ	ОК
Ki	  1	  100	. U0/t  4.105
Ku	. U0/t  4. 105	U0/t  4. 103	1
Kp	Ku. Ki  4. 105	Ku. Ki  4. 105	KuKi  4.105
Rвх	t/Iэ 26 Ом	. t/Iэ  2,5 кОм	. U0/Iк 10 МОм
Rвых	. U0/Iк 10 МОм	U0/Iк  100 кОм	t/Iэ 26 Ом

Анализ данных, представленных в табл. 5.3, показывает следующее.

1. Все схемы включения обеспечивают одинаковое усиление по мощности.

2. Включения с ОБ и ОК по соответствующим параметрам дополняют друг друга. Если схема с ОБ имеет минимальный K_i и максимальный K_u, то схема с ОК, наоборот, имеет минимальный K_u и максимальный K_i. То же самое наблюдается для входных и выходных сопротивлений. Эти особенности связаны с наличием в схемах с ОБ и ОК внутренней стопроцентной отрицательной обратной связи. Отличие заключается в типе связи: в схеме с ОБ – это параллельная по току, при которой обеспечивается малое входное и большое выходное сопротивления, а в схеме с ОК – последовательная по напряжению, при которой имеется большое входное и малое выходное сопротивления.

3. Схема с ОЭ позволяет усиливать сигналы как по току, так и по напряжению.

Рассмотрим методику составления и анализа МЭС и оценку усилительных параметров каскадов на примере схемы с ОЭ (рис. 5.9).

Рис. 5.9. МЭС усилительного каскада с ОЭ на БТ

1. Составляем МЭС БТ для схемы с ОЭ и пририсовываем к ней все внешние элементы, имеющиеся в исходной схеме, по правилам, изложенным выше. Получаем полную МЭС каскада (рис. 5.9).

2. Проводим следующие упрощения:

X_c = (1/C) << R, R1 >> r_э, R2 << r_к.

3. Выводим формулу для оценки Ku = uвых/uвх:

u_вых = i_кR2 = i_бR2 = R2u_вх/r_э.

Таким образом, K_u = R2/r_э, где r_э= _t/I_э.

4. Рассчитываем K_i = i_вых/i_вх. Так как i_вых = i_к, i_вх = i_б, то K_i = . При выводе этого соотношения использовано упрощение R₁>>r_э.

5. Полное входное сопротивление, наблюдаемое со стороны зажимов источника входного сигнала, складывается из X_c, параллельного соединения R1 и пересчитанного в цепь базы параллельного соединения r_э с последовательным соединением R2 и r_к. Однако в силу принятых допущений в конечном выражении будет присутствовать только пересчитанное в цепь базы дифференциальное сопротивление эмиттерного перехода R_вх  r_э = _t/I_э.

6. Для определения R_вых используем классический метод холостого хода и короткого замыкания (метод эквивалентного источника) и учтем введенные упрощения. При этом получаем

R_вых  R2r_к/(R2 + r_к)  R2.

На рис. 5.10 и 5.11 представлены принципиальные и малосигнальные схемы типовых усилительных каскадов с ОБ и ОК, а также формулы, позволяющие оценить усилительные параметры.

Рис. 5.10. Принципиальная и эквивалентная схемы усилительного каскада с ОБ

Рис. 5.11. Принципиальная и эквивалентная схемы усилительного каскада с ОК

Пример. Расчет усилительного каскада с ОЭ (рис. 5.6) со следующими исходными данными: напряжение питания E = 15 В, R2 = 2 кОм, C = 1 мкФ, частота входного сигнала равна 1000 Гц, транзистор с коэффициентом передачи тока базы  = 50. Требуется: а) оценить значение сопротивления R₁, при котором каскад работает в режиме класса А; б) рассчитать коэффициент усиления по напряжению K_u и в) определить, при каком уровне входного сигнала выходной сигнал начнет ограничиваться по амплитуде.

Решение. Сначала определяем координаты НРТ по формулам (5.6). Так как в данной схеме напряжение на базе равно напряжению отпирания БТ, то

U_ка = 0,5^. (15 + 0,6) = 7,8 В, I_ка = 0,5^. (15 - 0,6)/2 кОм = 3,6 мА.

Ток базы

I_ба = I_ка/ = 3,6 мА/50 = 72 мкА.

Искомое значение сопротивления

R1 = (E - U_б)/I_ба = (15 - 0,6)/72 мкА = 200 кОм,

что совпадает со значением, определяемым формулой (5.7).

Чтобы рассчитать K_u по формуле K_u = R2/r_э, необходимо сначала оценить дифференциальное сопротивление r_э = _t/I_э = 26 мВ/3,6 мА  7,2 Ом, тогда

K_u = (2 кОм/7,2 Ом)  280.

В режиме класса А максимальная амплитуда выходного сигнала ограничивается значением, при котором БТ начнет входить либо в режим отсечки, либо в режим двойной инжекции (точки "с" и "b" на рис. 5.7). Но так как в точке "с" напряжение на коллекторе равно напряжению питания E =15 В, а U_ка = 7,8 В, то максимальная амплитуда

U_вых = E – U_ка = 15 – 7,8 = 7,2 В.

Зная U_вых и K_u, определяем амплитуду входного сигнала, при которой выходной сигнал начнет ограничиваться:

maxU_вх = U_вых/K_u = 7,2/280  26 мВ.