
Рівняння математичної фізики
Довідковий матеріал
Задача Штурма-Лиувиля. Розглянемо крайову задачу
![]() , (1)
, (1)
![]()
![]() (2)
(2)
Тут
![]()
![]()
![]()
![]()
![]()
![]() параметри
параметри
![]() задовольняють умовам
задовольняють умовам
![]()
![]() потрібно знайти такі значення параметра
,
при яких існують відмінні від тотожного
нуля (нетривіальні) розв’язки
диференціального рівняння (1), які
задовольняють краєвим умовам (2).
потрібно знайти такі значення параметра
,
при яких існують відмінні від тотожного
нуля (нетривіальні) розв’язки
диференціального рівняння (1), які
задовольняють краєвим умовам (2).
Ті значення параметра , при яких існує нетривіальний розв’язок задачі (1)–(2), називаються власними значеннями цієї крайової задачі, а відповідні їм нетривіальні розв’язки – власними функціями.
Властивості власних значень та власних функцій
Існує зчисленнамножина власних значень
![]() при
при
![]() ,
,
яким відповідають власні функції
![]()
Власні функції на відрізку
 ,
які відповідають різним значення
параметра ,
ортогональні з вагою
,
які відповідають різним значення
параметра ,
ортогональні з вагою
 :
:

Теорема Стеблова. Всяка функція
 ,
яка задовольняє краєвим
умовам
(2) і, яка має неперервну першу похідну
та частинну-неперервну другу похідну,
розкладається в ряд, що абсолютно і
рівномірно збігається, за власними
функціями
,
яка задовольняє краєвим
умовам
(2) і, яка має неперервну першу похідну
та частинну-неперервну другу похідну,
розкладається в ряд, що абсолютно і
рівномірно збігається, за власними
функціями
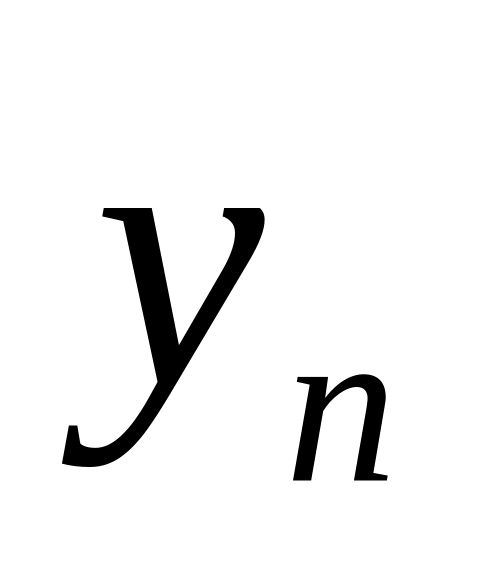 :
:
![]()

Для
прикладу розв’яжемо наступну задачу.
Знайти в заданій області відмінні від
тотожного нуля розв’язки
![]() диференціального рівняння, яке задовольняє
заданим краєвим умовам:
диференціального рівняння, яке задовольняє
заданим краєвим умовам:
![]() (3)
(3)
![]() (4)
(4)
Розглянемо три випадки.
 .
Загальний розв’язок рівняння (3) має
вид:
.
Загальний розв’язок рівняння (3) має
вид:

З умови
![]() знаходимо
знаходимо
![]()
![]()
З умови
![]() отримаємо
отримаємо
![]() ,
т. б.
,
т. б.
![]() ;
;
 Загальний
розв’язок рівняння (3) має вид:
Загальний
розв’язок рівняння (3) має вид:
 Умови (4) приводять до того, що
Умови (4) приводять до того, що
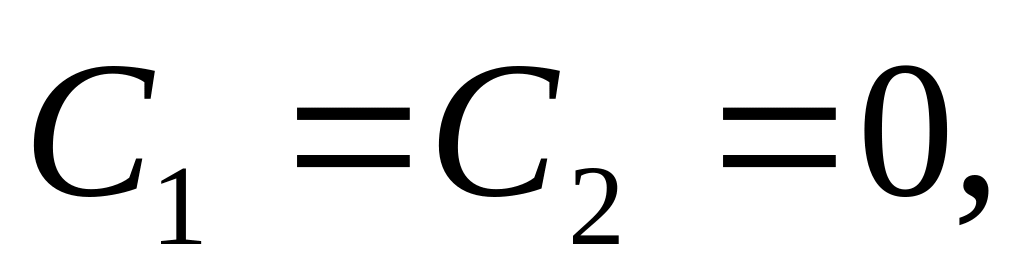 т. б.
;
т. б.
;Загальний розв’язок рівняння (3) має вид:
З умов
отримаємо
;
![]()
Умова
приводить до рівняння
![]() Так як
Так як
![]() і
і
![]() то
то
![]() звідки отримуємо:
звідки отримуємо:
![]() ;
таким чином, власні значення задачі
(3)–(4) рівні
;
таким чином, власні значення задачі
(3)–(4) рівні
![]() ,
власні функції –
,
власні функції –
![]()
Зведення до канонічного виду лінійних рівнянь з частинними похідними другого порядку у випадку двох незалежних змінних. Загальне лінійне рівняння з частинними похідними другого порядку з двома незалежними змінними має вид:
![]() (5)
(5)
де
![]() –
задані функції змінних х,
у.
Воно належить до еліптичного
типу
в точці (х,
у),
якщо
–
задані функції змінних х,
у.
Воно належить до еліптичного
типу
в точці (х,
у),
якщо
![]() належить до гіперболічного
типу
в точці (х,
у),
якщо
належить до гіперболічного
типу
в точці (х,
у),
якщо
![]() і належить до параболічного
типу в точці (х,
у),
якщо
і належить до параболічного
типу в точці (х,
у),
якщо
![]()
Рівняння
![]() (6)
(6)
називається
рівнянням
характеристик
для рівняння (5), а крайові, визначаються
співвідношенням
![]() де
–
розв’язок рівняння (6), називаються
характеристиками
рівняння (5).
де
–
розв’язок рівняння (6), називаються
характеристиками
рівняння (5).
Рівняння (6) еквівалентно двом рівнянням
![]() (7)
(7)
![]() (8)
(8)
Для
рівняння гіперболічного типу загальні
інтеграли
![]() і
і
![]() рівнянь (7) та (8) дійсні та різні; вони
визначають два різних сімейства дійсних
характеристик рівняння (5). Заміна
рівнянь (7) та (8) дійсні та різні; вони
визначають два різних сімейства дійсних
характеристик рівняння (5). Заміна
![]()
![]() приводить рівняння (5) до канонічного
виду:
приводить рівняння (5) до канонічного
виду:
![]() .
.
Якщо
рівняння належить до параболічного
типу, то рівняння (7) і (8) співпадають,
загальний інтеграл
![]() визначає одне сімейство дійсних
характеристик рівняння (5). Заміна
,
де
визначає одне сімейство дійсних
характеристик рівняння (5). Заміна
,
де
![]() - довільна, двічі неперервно диференційована
функція, яка задовольняє умові
- довільна, двічі неперервно диференційована
функція, яка задовольняє умові
![]() у області, що розглядається, приводить
рівняння до канонічного виду:
у області, що розглядається, приводить
рівняння до канонічного виду:
![]()
Для рівняння еліптичного типу загальні інтеграли рівнянь (7) і (8) є комплексно-спряженими. Вони визначають два сімейства уявних характеристик.
Нехай
![]() – загальний інтеграл рівняння (7). Тоді
заміна
приводить рівняння (5) до наступного
канонічного виду:
– загальний інтеграл рівняння (7). Тоді
заміна
приводить рівняння (5) до наступного
канонічного виду:
![]()
Зауваження. У деяких випадках канонічне рівняння дозволяє без труда знайти загальний розв’язок заданого рівняння.
Наприклад,
рівняння
![]() заміною
заміною
![]() приводиться до канонічного виду
приводиться до канонічного виду![]() .
Його загальний розв’язок задається
формулою:
.
Його загальний розв’язок задається
формулою:
![]()
отже, загальний розв’язок даного рівняння може бути записаний у вигляді
![]()
де
![]() - довільні двічі неперервно диференційовані
функції.
- довільні двічі неперервно диференційовані
функції.
Метод розділення змінних. Розглянемо використання цього методу до розв’язків рівнянь різних типів.
Еліптичні рівняння
Задача Діріхле для рівняння Лапласа крузі радіуса R:
![]()
![]()
де
![]() – полярні координати точки
– полярні координати точки
![]() ;
;
![]() – задана функція.
– задана функція.
В полярних
координатах
![]() рівняння Лапласа має вид
рівняння Лапласа має вид
![]() (9)
(9)
Розв’язок цього рівняння будемо шукати в вигляді
![]() (10)
(10)
Підставляючи вираз (10) в (9), отримаємо
![]() або
або
![]()
З
останнього співвідношення для знаходження
функцій
![]() і
і
![]() отримаємо звичайне диференціальне
рівняння
отримаємо звичайне диференціальне
рівняння
![]() (11)
(11)
![]() (12)
(12)
Із
очевидної рівності
![]() слідує, що
слідує, що
![]() з
рівняння (11) знаходимо
з
рівняння (11) знаходимо
![]() і
і
![]()
Загальний розв’язок рівняння (12) має вигляд
![]() при
при
![]()
![]() при
при
![]()
Через
обмеженість розв’язку
![]() у центрі круга маємо
у центрі круга маємо
![]() т. б.
т. б.
![]() при
при
![]() при
при
![]()
Розв’язок задачі Дирихле шукається у вигляді
![]()
де
коефіцієнти
![]() визначається за формулами:
визначається за формулами:
![]()
![]()
![]()
Зауваження. Розв’язок задачі Діріхле для рівняння Лапласа у кільці шукається у вигляді

Коефіцієнти визначаються із граничних умов.
Задача Діріхле для рівняння Лапласа у кулі радіуса R:
![]()
Тут
![]() – сферичні координати точки
– сферичні координати точки
![]()
![]() – задана функція.
– задана функція.
Частинні розв’язки рівняння Лапласа, записаного в сферичних координатах
![]() (13)
(13)
будемо
шукати у вигляді
![]() Підставляючи їх в (13), отримуємо рівняння
Підставляючи їх в (13), отримуємо рівняння
![]() (14)
(14)
![]() (15)
(15)
Будемо
шукати розв’язки рівняння (15) у вигляді
![]() .
З урахуванням співвідношення
.
З урахуванням співвідношення
![]() отримаємо:
отримаємо:
![]() (16)
(16)
![]() (17)
(17)
Із (16)
маємо
![]()
![]()
Поклавши
в (17)
![]() і позначаючи
і позначаючи
![]() ,
отримаємо
,
отримаємо
![]()
Це
рівняння має обмежені на відрізку
![]() розв’язки тоді і тільки тоді, коли
розв’язки тоді і тільки тоді, коли
![]() ,
і цими розв’язками є функції
,
і цими розв’язками є функції
![]()
де
![]() – поліноми Лежандра;
– поліноми Лежандра;
![]()
![]()
Таким чином ми знаходимо частинні розв’язки рівняння (15):
![]()
і
загальний розв’язок рівняння (14) при![]()
![]()
Отже, шукані частинні розв’язки рівняння (13) можуть бути представлені у вигляді:
![]()
Розв’язок задачі Діріхле для рівняння Лапласа у кулі потрібно шукати у вигляді:

де
![]()
![]() визначаються через коефіцієнти
розкладання функції
визначаються через коефіцієнти
розкладання функції
![]()

Зауваження 1. розв’язок задачі Діріхле для рівняння Лапласа в кульовому шарі слідує шукати у вигляді:


Коефіцієнти визначаються з граничних умов.
Якщо
граничні функції не залежать від кута
,
т. б.
![]() ,
то відповідні формули спрощуються:
,
то відповідні формули спрощуються:
![]() – у випадку кулі, де
– у випадку кулі, де
![]()
![]() – у випадку кульового шару.
– у випадку кульового шару.
Коефіцієнти визначаються з граничних умов.
Зауваження
2. Метод розподілу змінних, застосований
до рівняння Гельмгольца
![]() в кулі, приводить до розв’язку рівняння
в кулі, приводить до розв’язку рівняння
![]()
яке
змінною
![]() зводиться до рівняння Бесселя
зводиться до рівняння Бесселя

Зауваження
3 . Рівняння Пуассона
![]() заміною
заміною
![]() ,
де
,
де
![]() -
частинний розв’язок рівняння Пуассона,
зводиться до рівняння Лапласа
-
частинний розв’язок рівняння Пуассона,
зводиться до рівняння Лапласа
![]()
