14.3. Статистическая обработка результатов наблюдении

Надежность рудничного и взрывозащищенного электрооборудования, закладываемая в процессе проектирования и изготовления, реализуется только при эксплуатации. Поэтому наиболее полно и достоверно количественные показатели могут быть определены в результате статистической обработки информации об отказах. Основным источником информации о надежности изделий является сбор данных в производственных условиях, а также другие источники, подробно изложенные в [16].

В первую очередь при обработке статистической информации производят оценку анормальности результатов наблюдений. Анормальным называют результат, резко отличающийся от группы результатов наблюдений, которые признаются нормальными.

При оценке анормальных результатов следует иметь в виду, что резко отличающийся результат наблюдения мог быть получен в тех же условиях, что и остальные наблюдения, однако он является случайным событием с малой вероятностью появления. Такой результат должен быть исключен из выборки.

Если же установлено, что анормальный результат получен вследствие нарушения условий наблюдений или ошибок при учете, необходимо пересчитать результат для достоверных условий. Если это невозможно, результат из выборки исключается.

Для оценки анормальности результатов наблюдений полученную выборку случайных величин располагают в упорядоченный возрастающий вариационный ряд t₁≤t₂≤tз≤…≤t_N. вычисляют среднее арифметическое и среднее квадратическое отклонение σ всей выборки, включая и нормальные результаты. Определяют U-критерий Смирнова для крайних значений выборки t₁ и t_N:

Расчетные значения сравнивают с табличным значением критерияU_T для данного объема выборки при принятом уровне значимости α.

Если U₁≥U_t или U_N ≥U _T. результат из выборки исключается и дальнейшая обработка производится без учета t₁ и t_{N. .}Если же U ₁≤.U_T (U_N≤.U_T), то анормальный результат не исключается. Следует отметить, что такой способ оценки пригоден для нормального закона распределения случайных величин.

В процессе обработки собранные статистические данные сводятся в отдельные выборки по определенным информационным признакам. Полученные выборки проверяют на однородность.

Проверку гипотезы об однородности выборок проводят только для полных выборок, т. е. таких, в которых все изделия имели отказы или были отправлены в капитальный ремонт. Если же не все изделия имели отказы, такая выборка называется усеченной (неполной), для которой проверка гипотезы об однородности выборки не производится.

Понятие о полной и усеченной выборке применяют только для наработки на отказ и ресурса изделий. Для всех остальных показателей все выборки считаются полными.

Смысл проверки гипотезы заключается в установлении того, чем вызвана разница в данных между выборками: либо влиянием информационного признака, положенного в основу разделения выборок (сезонность, технологичность, условия эксплуатации), либо случайными причинами, которые определяются небольшим объемом испытаний.

Предположение о том, что различие между сравниваемыми величинами отсутствует, а наблюдаемые отклонения случайны, называют нулевой гипотезой. Гипотезы, отличные от нулевой, называют альтернативными. Нулевая гипотеза принимается или отвергается только при определенном уровне значимости или с определенной достоверностью.

При проверке гипотезы об однородности выборки по каждой из наличных выборок определяется среднее F-критерий Фишера F_ОП=σ₁²/σ₂² при σ₁<σ₂.

По таблицам F-распределения в зависимости от числа степеней свободы k₁ и k₂ для каждой выборки находят табличные значения F_T.

Число степеней свободы k₁ = n₁—1; k₂ = n₂—1, где п₁ и n₂—количество опытных данных по первой и второй выборкам.

При соотношении F _оп≥F_T гипотезу об однородности выборок и их принадлежности к одной генеральной совокупности отклоняют, так как существует неслучайная разница между дисперсиями выборок.

При F_ОП<.F_Т проводят дополнительную проверку по t-критерию Стьюдента:

где ₂—cредние арифметические значения выборок.

Следует иметь в виду, что нумерация выборок при расчете t-критерия часто не совпадает с их нумерацией при расчете F-критерия, так как не всегда наибольшему t двух выборок соответствует наибольшее .

По таблицам t распределения 32 в зависимости от числа степеней свободы k находят табличное значение t_T.При этом k=n₁+n₂-2.

Если t_ОП ≥ t_T, гипотезу об однородности выборок отклоняют из-за существенной разницы между средними арифметическими выборок. При tоп<t_т выборки считаются однородными.

Осуществляя последовательный перебор всех пар выборок с учетом технических ограничений, подбирают однородные выборки и объединяют их для дальнейшей обработки. Неоднородные выборки обрабатываются в отдельных случаях для технико-экономических расчетов (ТЭР).

После проверки гипотезы об однородности выборки по формулам (14.9) — (14.16) определяются показатели надежности: наработка на отказ Т, интенсивность отказов, вероятность безотказной работы Р(t), средний ресурс до капитального ремонтаТ к и др.

Точность оценки показателей надежности определяется доверительным интервалом и доверительной вероятностью.

Если генеральную совокупность из N изделий разделить на несколько выборок по п изделий в каждой, выборочные средние арифметические в силу случайных отклонений показателей надежности распределяются в некотором интервале от t _min до t_max. Любое из этих средних с равной достоверностью характе­ризует генеральную совокупность.

Если же из генеральной совокупности испытана одна выборка, ее выборочное среднее характеризует эту совокуп­ность с определенной ошибкой.

Для оценки этой ошибки назначают большую вероятность α = 0,8÷0,99 и считают событие с такой вероятностью достоверным. Затем находят значения выборочного среднего, у которых диапазон отклонений от среднего значения генеральной совокуп­ности равен ±ε:

.

Таким образом, значение t _Г.c попадает в интервал ± ε.

Средняя арифметическая величина генеральной совокупности является не случайной, однако случайно положение интервала. Поэтому α представляют как вероятность того, что случайный интервал «накрыл» точку t _Г,C (рис. 14.8).

Вероятность α называют доверительной, интервал I_α—доверительным интервалом, а точки —ε и + ε—доверительными границами. Ширина доверительного интервала характеризует точность выборочной оценки генеральной совокупности, а доверительная вероятность—достоверность оценки.

Доверительные интервалы для средних арифметических оценок наработки на отказ, среднего времени восстановления и др. определяются соотношениями:

1) при экспоненциальном законе

невосстанавливаемые изделия

восстанавливаемые изделия

2) при нормальном законе

3) при законе Вейбулла

где

• r₁, r₂, r₃ — коэффициенты, определяемые по таблицам [32] в зависимости от N и доверительной вероятности α;

• t_α— коэффициент Стьюдента, определяемый в зависимости от числа степеней свободы k = N—1 и α.

Если за время эксплуатации отказов не было, среднее время эксплуатации определяют по формуле

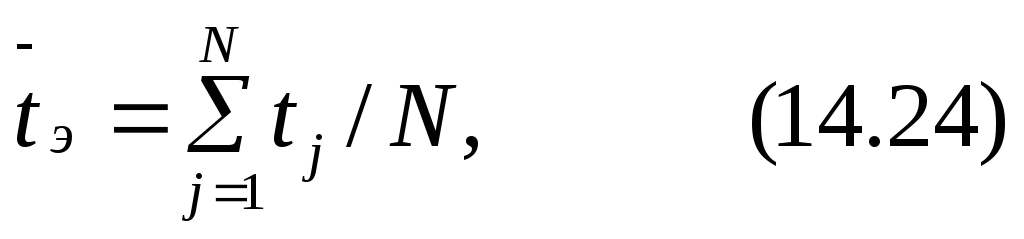
где t _j—время безотказной работы j-го изделия.

Затем находят нижнюю доверительную границу среднего арифметического показателя безотказности

где —табличное отношение нижней доверительной границы к средней продолжительности эксплуатации [32].

Полученные показатели надежности считаются приемлемыми, если требуемое значение окажется внутри доверительного интервала. При этом точность выборочной оценки должна быть не менее 0,05—0,10, а доверительная вероятность -в пределах 0,80—0,95.

Минимальное количество изделий, необходимое для получения достоверного результата, определяется в зависимости от того, известен или нет закон распределения случайной величины. В связи с этим различают параметрический (при известном законе) и непараметрический метод определения объема испытаний.

При параметрическом методе необходимое число испытуемых изделий определяется по выражениям:

1)при экспоненциальном распределении

2)при нормальном законе

3)при законе Вейбулла

где

• δ_О—заданная относительная ошибка среднего показателя надежности (0,01—0,20), равная половине относительной длины доверительного интервала;

• n—минимальное число наблюдае­мых изделий;

• v—ожидаемый коэффициент вариации показателя надежности;

• X²i—α:

• 2n—табличное значение критерия Пирсона при степенях свободы k₁=1 — α;

• k₂ = 2n [32];

• t _α- _n-1 -табличное значение критерия Стьюдента при степенях свободы k₁=a;

• k₂ = n—1 [32].

При непараметрическом методе, когда закон распределения неизвестен, число образцов

где P(t)—вероятность безотказной работы за время t, которую требуется подтвердить в результате наблюдений.

Статистические данные необходимы прежде всего для установления статистического закона распределения случайной величины и последующего сопоставления его с известными теоретическими законами, что позволит определить количественные показатели надежности.

Гипотезу о законе распределения проверяют одним из следующих методов: сравнением гистограмм плотности распределения, интенсивности и вероятности случайной величины с типовыми теоретическими графиками для различных законов; по координатной сетке с вероятностной шкалой и критерию согласия Колмогорова; по критерию согласия Пирсона.

Для построения гистограммы необходимо :

• собранные данные расположить в упорядоченный возрастающий вариационный ряд и разделить его на несколько интервалов;:

• число интервалов r в зависимости от количества данных в выборе принять:

• определить длину интервала

где и— соответственно наименьшее и наибольшее значение случайной величины в упорядоченном вариационном ряду.

Для каждого интервала в табличной форме определяют следующие данные:

где —число значений случайной величины, приходящееся наi-й интервал;

-общее число значений случайной величины от первого до начала и конца i-го интервала;

Строят гистограммы f_i*; λ _i*; F_i*, для чего на оси абсцисс откладывают в определенном масштабе интервалы Δt_i, а на оси ординат—соответствующее значение величины.

Сравнивая построенную статистическую гистограмму с графиками теоретических функций для различных законов, ориентировочно устанавливают, к какому теоретическому закону наиболее близко полученное распределение.

При небольших выборках (п<20) вместо гистограмм строят кривые убыли соответствующих функций [2].

При проверке гипотезы по критерию согласия Пирсона на основании расчетной таблицы определяют меру расхождения между статистическими значениями плотности распределения и ее теоретическим значением

где P_i—теоретическая вероятность попадания случайной величины в i-й интервал для проверяемого закона распределения;

F(t)—теоретические функции распределения для проверяемого закона:

• экспоненциального

• нормального

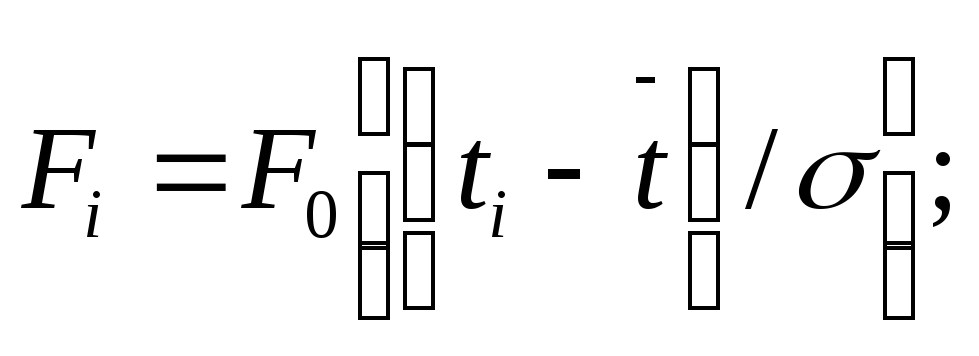
• Вейбулла

Помимо меры расхождения х² определяют число степеней свободы k = r—1 —W, где W— число параметров случайной величииы, по которым требуется проверить совпадение статистических данных с теоретическим законом.

Для экспоненциального закона W=1, для остальных W=2.

Рассчитав х² и k, определяют их отношение и по таблице критерия Пирсона принимают ближайшее значение.

Если вероятность P = f(x²/k) мала, согласие статистических данных с рассматриваемым теоретическим распределением хорошее, и наоборот.

Если аппроксимирующая кривая согласуется с несколькими теоретическими законами, предпочтение отдается наиболее простому распределению с наименьшим числом параметров.

Когда статистические данные не согласуются ни с одним из законов, уточняют однородность выборки или продолжают наблюдения для получения дополнительных данных.