
- •Дисциплина «Теория вероятностей и матстатистика» Контрольная работа
- •«Теория вероятностей и математическая статистика» вариант №1 Задача 1
- •Задача 2
- •Задача 3
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №2 Задача 12
- •Задача 13
- •Задача 14
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №3 Задача 23
- •Задача 24
- •Задача 25
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №4 Задача 34
- •Задача 35
- •Задача 36
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №5 Задача 45
- •Задача 46
- •Задача 47
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №6 Задача 56
- •Задача 57
- •Задача 58
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №7 Задача 67
- •Задача 68
- •Задача 69
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №8 Задача 78
- •Задача 79
- •Задача 80
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №9 Задача 89
- •Задача 90
- •Задача 91
- •Выборка
- •Выборка
- •«Теория вероятностей и математическая статистика» вариант №10 Задача 100
- •Задача 101
- •Задача 102
- •Выборка
- •Выборка
Дисциплина «Теория вероятностей и матстатистика» Контрольная работа
Контрольная работа оформляется в соответствии с предложенными заданиями в той последовательности, в которой задания предлагаются для выполнения. Условия задания должны быть перенесены в файл, после чего должно следовать решение задачи с необходимыми пояснениями и достаточной степенью подробности.
На титульном листе должны быть указаны следующие данные: специальность, курс, идентификатор студента, фамилия, имя, отчество студента, вариант.
Номер варианта выбирается в соответствии с тремя последними цифрами идентификатора. Если идентификатор (три последние цифры) больше количества вариантов заданий, то номер варианта рассчитывается делением идентификатора (три последние цифры) на количество вариантов и остаток от деления – это Ваш вариант. Если остаток от деления равен нулю, то Ваш вариант соответствует последнему номеру варианта лабораторной работы. (Пример. Идентификатор – m02e1g1-025. Количество вариантов – 14. Расчет: 25:14=1 с остатком 11. Ваш вариант – 11).
Оформлять контрольную работу необходимо при помощи компьютерных редакторов и представлять в электронном виде для регистрации на учебном Web-сайте.
Обязательное требование - имя отчетного файла должно содержать только латинские символы (пример: lab3vmat.doc).
«Теория вероятностей и математическая статистика» вариант №1 Задача 1
Даны независимые случайные величины:
|
|
1 |
2 |
3 |
|
|
-2 |
-1 |
0 |
|
0.2 |
0.3 |
0.5 |
|
0.6 |
0.2 |
0.2 |
Составить распределения их суммы
 и произведения
и произведения
 ;
;Найти математические ожидания
 ,
,
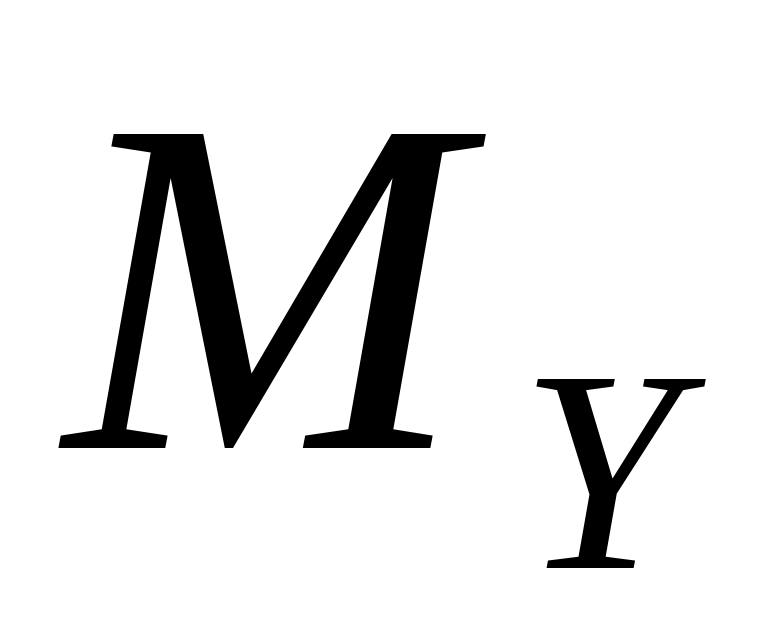 ,
,
 ,
,
 ;
;Найти дисперсии
 ,
,
 ,
,
 ,
,
 ;
;Проверить:
= +
=
= +
Задача 2
Дана таблица, определяющая закон распределения системы двух случайных величин ( , ):
|
20 |
40 |
60 |
10 |
2 |
3 |
0 |
20 |
|
2 |
5 |
30 |
4 |
2 |
2 |
Найти:
коэффициент ;
математические ожидания и ;
дисперсии и
 ;
;коэффициент корреляции
 .
.
Задача 3
Выполнить следующие действия по выборкам
![]() и
и
![]() :
:
Составить вариационный ряд;
Вычислить относительные частоты и накопленные частости;
Построить графики вариационного ряда (полигон, гистограмму, кумулянту);
Составить эмпирическую функцию распределения;
Построить график эмпирической функции распределения;
Вычислить числовые характеристики ряда:
Среднее арифметическое
 ;
;Дисперсию
 ;
;Среднеквадратичное отклонение
 ;
;Моду;
Медиану.
Задача 4
Вычислить несмещенные оценки параметров
генеральной совокупности
![]() ,
,
![]() и
и
![]() по выборкам
и
,
используя результаты , полученные в
задаче 3.
по выборкам
и
,
используя результаты , полученные в
задаче 3.
Задача 5
Найти доверительные интервалы для среднего значения , дисперсии и среднеквадратичного отклонения генеральных совокупностей при доверительной вероятности 0,8, если из генеральной совокупности сделаны выборки , используемые в задаче 3.
Задача 6
По первому столбцу
![]() выборки
выборки
![]() при условии значимости
при условии значимости
![]() проверить гипотезу
проверить гипотезу
![]() о среднем значении:
о среднем значении:
![]() (где
(где
![]() равно целой части
равно целой части
![]() ),
при альтернативной гипотезе
),
при альтернативной гипотезе
![]() :
:
![]() ,
если задано
,
если задано
![]() .
.
Задача 7
По первому столбцу
![]() выборки
при уровне значимости
выборки
при уровне значимости
![]() проверить гипотезу
о среднем значении:
(где
равно целой части
проверить гипотезу
о среднем значении:
(где
равно целой части
![]() .),
при альтернативной гипотезе
:
.),
при альтернативной гипотезе
:
![]() ,
если стандартное отклонение
неизвестно.
,
если стандартное отклонение
неизвестно.
Задача 8
По первому столбцу
![]() выборки
при уровне значимости
выборки
при уровне значимости
![]() проверить гипотезу
о дисперсии:
проверить гипотезу
о дисперсии:
![]() ,
при альтернативной гипотезе
:
,
при альтернативной гипотезе
:
![]() ,
если
,
если
![]() равно целой части
равно целой части
![]() .
.
Задача 9
По первым двум столбцам
выборки
![]() при уровне значимости
при уровне значимости
![]() проверить сначала гипотезу о равенстве
дисперсий, и, если она принимается, то
проверить потом гипотезу о равенстве
средних значений.
проверить сначала гипотезу о равенстве
дисперсий, и, если она принимается, то
проверить потом гипотезу о равенстве
средних значений.
Задача 10
По выборке при уровне значимости проверить гипотезу о распределении Пуассона соответствующей генеральной совокупности.
Задача 11
По выборке при уровне значимости проверить гипотезу о нормальном распределении соответствующей генеральной совокупности.
Выборка
2 |
2 |
3 |
4 |
3 |
2 |
7 |
3 |
2 |
2 |
2 |
0 |
2 |
3 |
1 |
5 |
3 |
1 |
0 |
2 |
5 |
2 |
5 |
2 |
4 |
5 |
3 |
2 |
1 |
1 |
0 |
2 |
3 |
4 |
2 |
3 |
4 |
3 |
5 |
0 |
3 |
2 |
2 |
1 |
1 |
3 |
6 |
1 |
5 |
4 |
2 |
5 |
3 |
1 |
2 |
2 |
5 |
0 |
1 |
3 |
1 |
3 |
5 |
3 |
2 |
0 |
1 |
2 |
2 |
|
(![]() =69,
начало первого интервала: 0; длина
интервала: 1 )
=69,
начало первого интервала: 0; длина
интервала: 1 )
