
- •6. Переходные процессы в линейных электрических цепях
- •6.1. Общие сведения о переходных процессах
- •6.2. Законы коммутации и начальные условия
- •6.3. Составление интегродифференциальных уравнений
- •6.4. Решение дифференциальных уравнений
- •6.5. Переходные процессы в электрических цепях I порядка
- •6.6. Переходные процессы в электрических цепях II порядка
- •7. Электрические цепи периодического несинусоидального тока
- •7.1. Общие сведения
- •7.2. Разложение периодических функций в ряд Фурье
- •7.3. Спектры некоторых периодических колебаний
- •7.4. Расчет электрических цепей несинусоидального тока с использованием разложения в ряд Фурье
- •7.5. Действующее значение и мощность периодического несинусоидального тока
- •8. Линейные четырехполюсники
- •8.1. Системы уравнений четырехполюсников
- •8 Рис. 8.4. Соединение четырехполюсников: а – последовательное, б – параллельное, в – каскадное .2. Характеристики линейных четырехполюсников
- •8.3. Примеры линейных четырехполюсников
7.4. Расчет электрических цепей несинусоидального тока с использованием разложения в ряд Фурье
Пусть требуется рассчитать ток в электрической цепи под действием периодической несинусоидальной ЭДС
![]() , (7.10)
, (7.10)
где
![]() – амплитуда n-й
гармоники ЭДС. В линейных электрических
цепях токи в ветвях находятся методом
наложения (суперпозиций), путем
суммирования токов, создаваемых каждым
из слагаемых ЭДС (7.10). Для случая цепи,
состоящей из последовательного соединения
R,
L,
С элементов (рис. 7.13), имеем
– амплитуда n-й
гармоники ЭДС. В линейных электрических
цепях токи в ветвях находятся методом
наложения (суперпозиций), путем
суммирования токов, создаваемых каждым
из слагаемых ЭДС (7.10). Для случая цепи,
состоящей из последовательного соединения
R,
L,
С элементов (рис. 7.13), имеем
![]() ,
,
г
Рис. 7.13.
Последовательный колебательный контур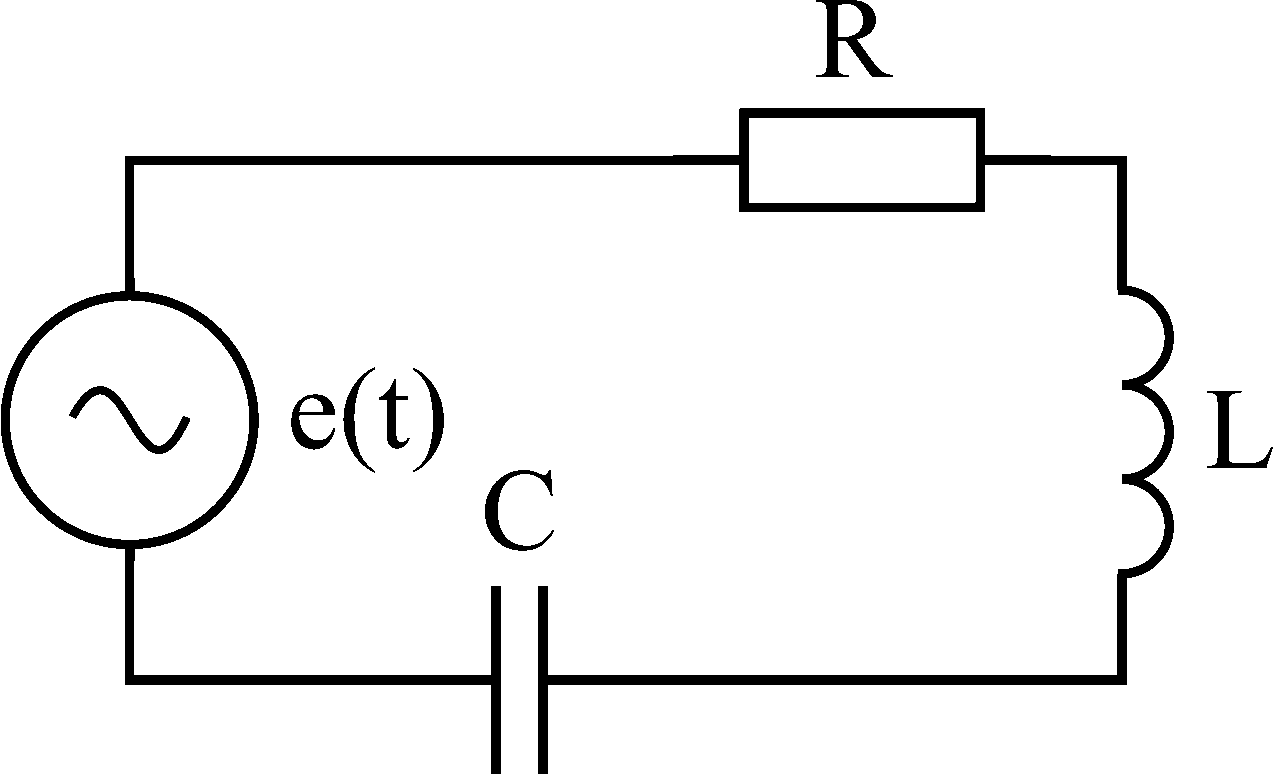
![]() – амплитуда n-й
гармоники тока,
– амплитуда n-й
гармоники тока,
![]() – полное сопротивление
цепи на частоте
– полное сопротивление
цепи на частоте
![]() ,
,
![]() .
.
Сопротивление
цепи на постоянном токе
![]() равно
равно
![]() ,
поэтому постоянная составляющая тока
,
поэтому постоянная составляющая тока
![]() .
При увеличении номера гармоники, т.е. с
увеличением частоты
.
При увеличении номера гармоники, т.е. с
увеличением частоты
![]() ,
индуктивное сопротивление возрастает
,
индуктивное сопротивление возрастает
![]() ,
а емкости уменьшаются
,
а емкости уменьшаются
![]() ,
поэтому полное сопротивление цепи
является функцией частоты
,
поэтому полное сопротивление цепи
является функцией частоты
![]() .
Если при некотором значении n
выполняется условие
.
Если при некотором значении n
выполняется условие
![]() ,
на частоте
возникает резонанс напряжения.
,
на частоте
возникает резонанс напряжения.
Расчет разветвленной цепи периодического несинусоидального тока ведется для каждой гармоники в символической форме. Полный ток находится суммированием мгновенных значений гармоник тока в ветвях, так как векторы комплексных токов имеют различную частоту вращения.
7.5. Действующее значение и мощность периодического несинусоидального тока
Действующее значение периодических токов (напряжений) определяется выражением
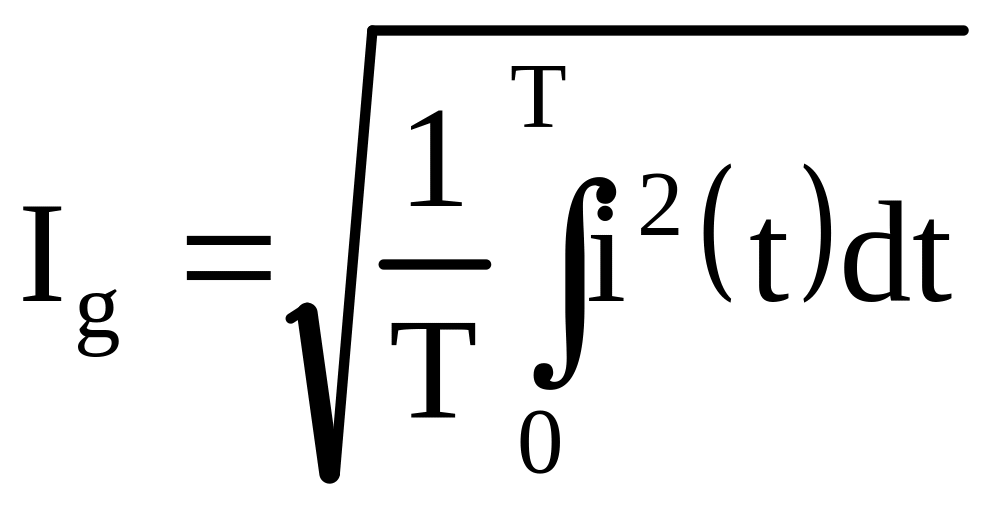 . (7.11)
. (7.11)
Для синусоидального тока действующее значение тока вычисляется по формуле
![]() .
.
В случае периодического несинусоидального тока вычисления по формуле (7.11) с использованием разложения в ряд Фурье дают результат
![]() . (7.12)
. (7.12)
Так как
![]() – квадрат действующего значения n-й
гармоники, (7.12) можно записать в виде
– квадрат действующего значения n-й
гармоники, (7.12) можно записать в виде
![]() . (7.13)
. (7.13)
Таким образом, действующее значение периодического несинусоидального тока равно корню квадратному из суммы квадратов действующих значений гармоник, включая постоянную составляющую. Активная мощность периодического несинусоидальго тока также может быть рассчитана с использованием разложения в ряд Фурье. Известно, что активная мощность равна среднему значению мощности за период
![]() . (7.14)
. (7.14)
При разложении периодических токов и напряжений в ряд Фурье средняя мощность каждой гармоники рассчитывается по формуле
![]() , (7.15)
, (7.15)
где n – сдвиг фазы между током и напряжением n-й гармоники. Интегрирование по формуле (7.14) с учетом ортогональности гармонических функций дает
![]() .
(7.16)
.
(7.16)
Из (7.16) следует, что активная мощность в цепях периодического несинусоидального тока равна сумме активных мощностей отдельных гармоник и мощности постоянной составляющей. Для несинусоидальных токов также используют такие параметры, как коэффициент формы, коэффициент амплитуды и коэффициент гармоник. Коэффициент формы определяется как отношение действующего значения тока к среднему значению:
 . (7.17)
. (7.17)
Для синусоидального
тока
![]() .
Коэффициент амплитуды определяется
как отношение максимального значения
к действующему значению:
.
Коэффициент амплитуды определяется
как отношение максимального значения
к действующему значению:
 . (7.18)
. (7.18)
Для синусоидального
тока
![]() .
.
Коэффициент гармоник определяется выражением
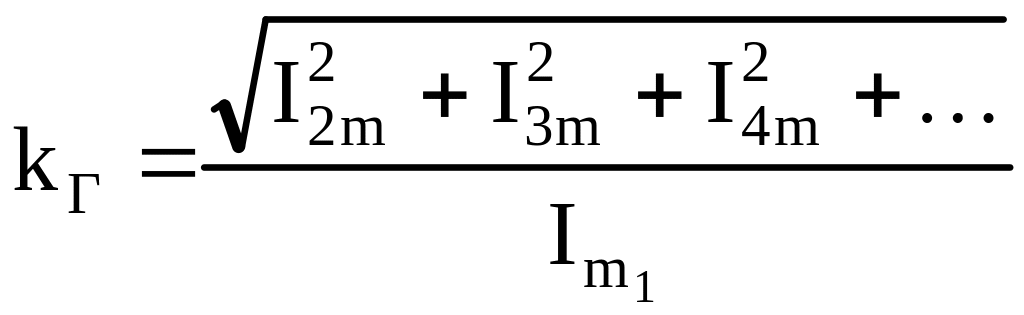 . (7.19)
. (7.19)
Коэффициент гармоник используется для оценки степени соответствия периодического тока синусоидальному току.
