Варианты мп-автоматов (доопределение)

То, что проходим с верхнего символа магазина не зависит от того, что находится под ним:

Знак " " соответствует знаку "|-".

Рассмотренным МП-автоматом называется цепочка символов , где d - отображение.

, - множество символов.

.

Если известно количество начальных символов, то можно, считав половину, установить маркер (е – такт).

е - такт из входной цепочки символов не считывает.

Автомат заносит некоторую часть цепочки (1/2), затем верхним символом становится некоторый маркер – S, указывающий положение середины цепочки. Далее помещаем очередной входной символ в магазин и осуществляем замену по правилу: .

Эквивалентность мп-автоматов и кс-грамматик

Нужно показать, что МП-автомат построен именно для КС-грамматик (контекстно-свободных). Пусть мы имеем КС-грамматику:

и пусть в этой грамматике есть правило .

Построить автомат, который определяет язык , генерируемый данной грамматикой:

1. .

2. .

3. .

П

ример:

E:=E+T

E:=T

T:=T*F

T:=F

F:=(E)

F:=i

q₀ – начальное состояние; z₀:=E – начальный символ магазина;

q₂ – заключительное состояние.

Рассмотрим i*i+i:

Мп, работающий снизу вверх

Рассмотрим i+i*i в грамматике G(E). Рассмотрим правый вывод этой цепочки:

E=>E+T=>E+T*F=>+i+i*i.

Цепочка i+i*i сворачивается к цепочке F+i*i по правилу F:=i. Это левая свертка.

Формальное определение для левой свертки

Пусть - грамматика. - правый вывод в ней, и имеется правило . Говорят, что правовыводимую цепочку можно свернуть слева к цепочке с помощью правила .

Восходящий распознаватель

По КС-грамматике можно построить эквивалентный расширенный МП-автомат, работа которого заключается в отсечении основ. Для этого случая удобно представить магазин в виде цепочки, верхним символом которой является самый правый. Конфигурация автомата остается прежней, а отношения перехода несколько меняются.

П

усть есть автомат: 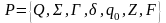; 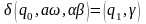. Отношения перехода будут иметь вид: 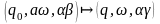, т.е. верхний символ становится справа.

E:=E+T;

E:=T;

T:=T*F;

F:=(E);

F:=i.

Введем символ «маркер дна» - $, который не принадлежит грамматике, добавим его в магазин.

Автомат не сработал. Надо было не заменять в точке, а продолжать грузить дальше.

Рассмотрим цепочку i+i*i

Детерминированный мп-автомат

Среди рассмотренных ранее автоматов большинство было недетерминированных, т.е. в текущей конфигурации при следующем такте нужно было выбрать вариант конфигурации.

МП-автомат называется недетерминированным, если для содержит не более одного состояния, и - содержит не более одного состояния (обозначается: ).

Проблема зацикливания

Конфигурация автомата для называется зацикливающийся, если существует такое состояние

.

Автомат ничего не считывает, а конфигурация магазина или растет, или не уменьшается.

3.4.1. Общие методы синтаксического анализа.

Для КС – грамматики входная цепочка разобрана (проанализирована), если известно дерево вывода. Но большинство компиляторов производит разбор моделированием МП – автомата, анализирующего цепочки либо сверху вниз, либо снизу вверх.

Способность МП – автомата проводить нисходящий разбор связана со способностью МП – распознавания отображать входные цепочки в последовательность левых выводов.

Восходящий разбор связан с отображением входной цепочки в последовательность обращенных правых выводов.

Проблему разбора теперь можно трактовать как последовательность левых или правых выводов.

Пусть G(N, S, P, S) – грамматика, правила которой занумерованы 1, 2 … р.

Пусть a - некоторая цепочка в этой грамматике, где a Î (NÈS*).

Тогда левый разбор цепочки a есть последовательность правил, примененных при левом выводе. S => +a.

Тогда правый разбор цепочки a - обращенная последовательность правил, примененных при правом выводе.

2 3 4 6 5 1 2

1) E:= E+T E =>T =>T*F =>F*F =>i*F =>i*(E) =>i*(E+T) =>i*(T+T) =>

2) E:=T 4 6 4 6

3) T:=T*F =>i*(F+T) =>i*(i+T) =>i*(i+F) =>i*(i+i).

4) T:=F;

5) F:=(E);

6) F:=i.

Левый разбор: 2 3 4 6 5 1 2 4 6 4 6.

2 3 5 1 4 6 2

E =>T =>T*F =>T*(E) =>T*(E+T) =>T*(E+F) =>T*(E+i) =>T*(T+i) =>

4 6 4 6

=>T*(F+i) =>T*(i+i) =>F*(i+i) =>i*(i+i).

Правый разбор: 6 4 6 4 2 6 4 1 5 3 2.

+

П

+

усть имеем G(N, S, P, S) - грамматику и занумерованные правила (см. выше).

Будем писать a_i Þ b_L , если это левый вывод и a_i Þ b_R , если правый.