ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра телекоммуникационных систем

Курсовая работа по дисциплине:

«Электромагнитные Поля и Волны»

Вариант 18

Выполнил: студент ФАП

гр. РРиТ-305 Шафикова А.Г.

Принял: профессор КТС

Загидулин Р.В.

Уфа 2007

Часть 1

Задание стр.3

1. Расчёт проводимости системы на единицу длины.Нахождение

тока утечки. стр.4

2. Расчёт и построение графиков распределения напряженности

электрического поля и потенциала в плоскости KF стр.5

3. Расчет и построение вектора плотности тока в точке М стр.7

4. Построение эквипотенциали с потенциалом 0.25U стр.8

Вывод стр.9

Часть 2

Задание стр.10

1. Определение плотности тока и напряженности магнитного

поля при частоте f стр.10

2. Определение плотности тока и напряженности магнитного

поля при частоте nf стр.12

3. Построение графиков зависимости модулей плотности

тока и напряженности магнитного поля от r стр.13

Вывод стр.15

Часть 3

Задание стр.16

1. Построение полярной диаграммы стр.16

2. Запись выражений для мгновенных значений векторов

напряженности электрического и магнитного полей в

точках А и В стр.18

Вывод стр.20

Часть № 1.

Задание:

1. Рассчитать проводимость системы на единицу длины. Найти ток утечки.

2. Рассчитать и построить графики распределения напряженности электрического поля и потенциала в плоскости KF.

3. Рассчитать и построить вектор плотности тока в точке М.

4. Провести эквипотенциаль с потенциалом, равным 0,25U, где U – приложенное напряжение.

Исходные данные:

Рисунок 8

R = 2,8 мм = 2,8·10^-3 м;

d = 50 мм = 0.05 м;

h = 28 мм = 0,028 м;

U = 370 В;

σ = 1*10^-5 См/м

Рис.1.1. Симметричная пара с радиусом жилы R₁ расположена в среде с проводимостью .

Задача о поле двухпроводной линии сводится к задаче о поле двух заряженных осей. Расчет задачи проводим при помощи метода зеркальных изображений. Его суть заключается в следующем. В результате электростатической индукции на проводящей поверхности выступают заряды. Для расчета такой системы кроме заданных заряженных осей вводят ещё дополнительную фиктивную пару осей, линейные плотности зарядов которых будут равными по значению, но противоположные по знаку зарядам в реальной паре.

1.

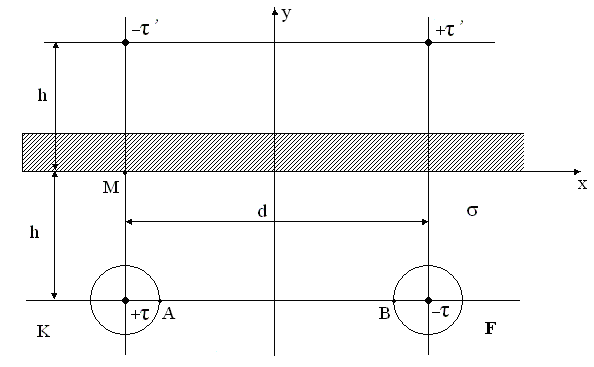
Рис.1.2. Симметричная пара с радиусом жилы R₁ расположена в среде с проводимостью  и её зеркальное отображение.

Потенциал в любой точке:

Константу С находим из условия: х=0, y=0, φ=0 (оси - эквипотенциальные поверхности с нулевым потенциалом)

Емкость системы на единицу длины:

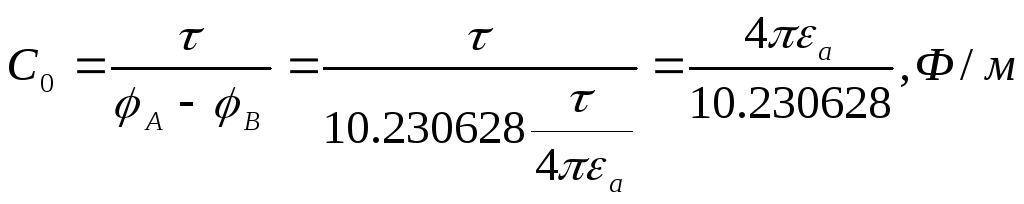
Проводимость системы на единицу длины:

Ток утечки:

2. Потенциал в любой точке определяется по формуле:

Так как , то для нахождения и продифференцируем выражение по x и y, получим:

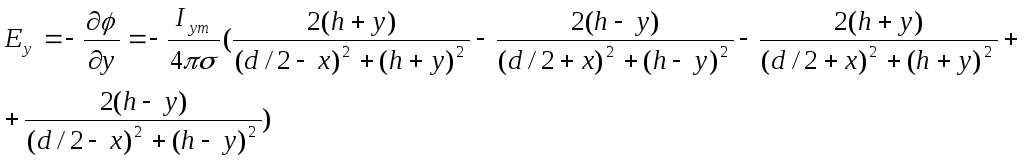
Подставим числовые значения. В плоскости KF потенциал и напряженность электромагнитного поля будут зависеть только от x, т. к. y=const= -28 мм:

При построении графика зависимости E от x будем учитывать только х-овую составляющую, т. к. максимальное значение, принимаемое функцией E_y(x, -28) не превышает по модулю 1 В/м, а вычисление векторной суммы х-овой и y-овой составляющих связано со значительными математическими трудностями.

Рис. 1.3. График распределения потенциала в плоскости KF.

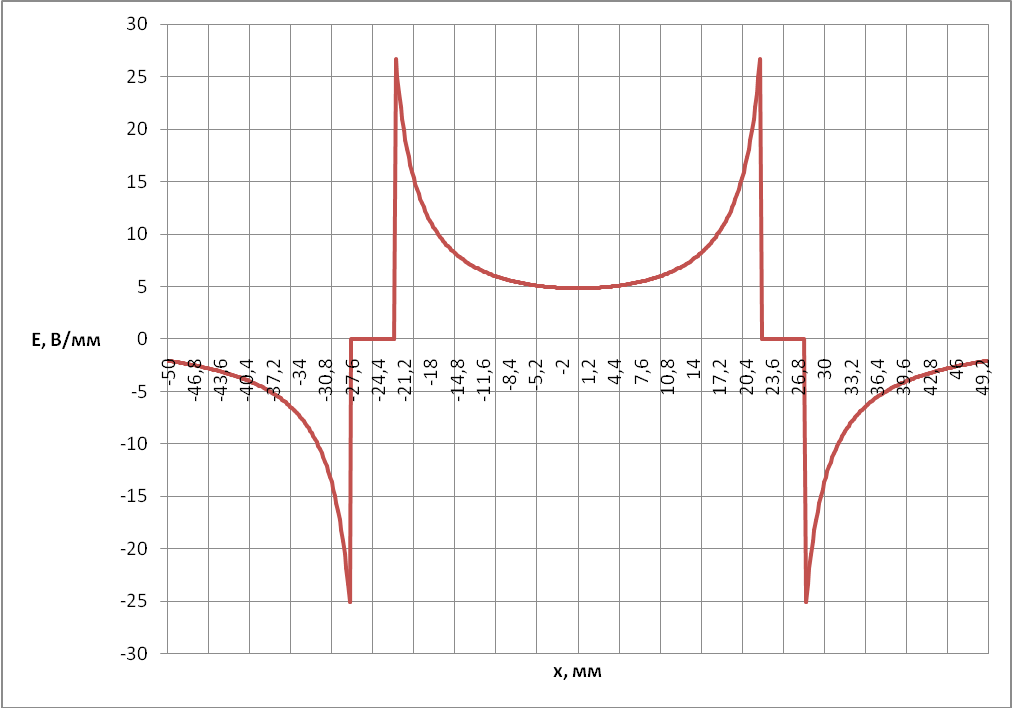
Рис. 1.4. График распределения напряженности электрического поля в плоскости KF.

3. Точка М имеет координаты x = -25; y = 0.

Напряженность поля в точке М:

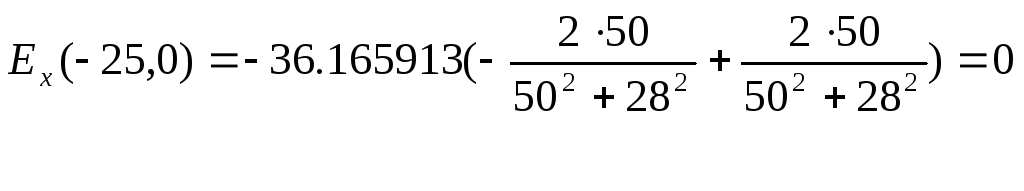
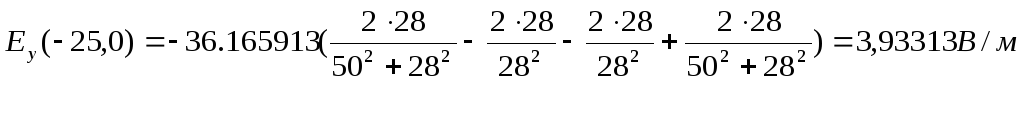
Модуль напряженности поля в точке М:

E=E_y=3,93313 В/м.

Вектор плотности тока:

Модуль вектора плотности тока:

j = 3,93313 ·10^-5 В/м²

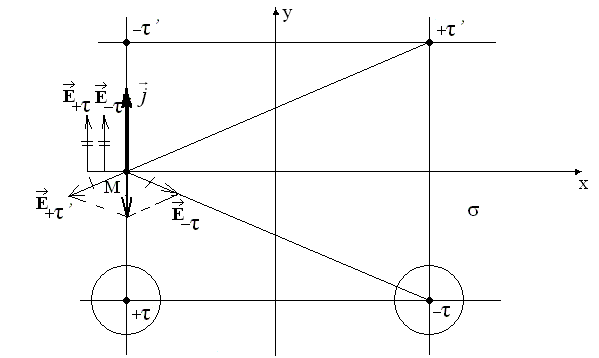
Рис. 1.5. Вектор плотности тока.

4. φ=0,25U=0,25·370=92,5 В

Потенциал в любой точке:

График, являющийся решением этого уравнения приведен на рис.1.6.

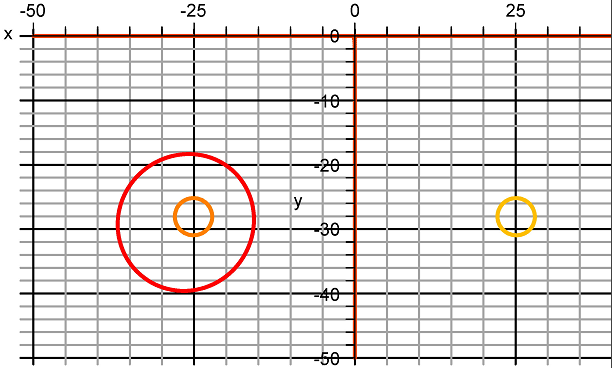
Рис.1.6. Чертеж эквипотенциали.

Выводы:

• Наибольшее значение Е(х) на поверхности проводников.

• При расчете и построении вектора плотности тока в точке М выяснили, что он имеет только y-составляющую.

• Эквипотенциаль определяется уравнением четвёртого порядка и представляет собой эллиптическую фигуру.

Часть № 2.

Исходные данные:

Im=2,6А; R=3,0мм=310-3м; =3,75107 Cм/м; =100; f=200Гц; n=13.

Амплитудное значение синусоидального тока; Радиус проводника; Удельная проводимость материала; Относительная магнитная проницаемость; Частота; Коэффициент.

По круглому цилиндрическому проводнику протекает синусоидальный ток i=I_m sin t, А.

Радиус проводника R, удельная проводимость материала , относительная магнитная проницаемость .

Определить плотность тока и напряженность магнитного поля внутри проводника. Числовой ответ дать для точек, находящихся на расстоянии от оси провода r=0; r=0,25R; r=0,5R; r=0,75R; r=R при двух частотах: f и nf.

Построить графики зависимостей модулей плотности тока и напряженности магнитного поля от r.

Рис.2.1. Проводник по которому течёт ток.

1. Определим плотность тока и напряженность магнитного поля внутри проводника при f=250Гц.

Предполагаем, что обратный провод не влияет на поле в прямом.

Для цилиндрического проводника плотность тока определяется по формуле:

, где

j_m0 – амплитудное значение плотности тока на оси провода.

Напряжённость магнитного поля равна:

Бесселевы функции J₀(qr) и J₁(qr) от комплексного аргумента

тоже являются комплексами и могут быть представлены в показательной форме:

,

где b₀-модуль, а β₀—аргумент функции J₀(qr); b₁-модуль, а β₁—аргумент функции J₁(qr).

Аргументами β₀ и β₁ пренебрегаем и не используем в вычислениях, т.к. графики строятся по значению модуля функции Бесселя. Т.е. запишем это в виде:

Заряд считаем по формуле:

ω = 2πf = 23,14200 = 1256,637 рад/с

μ_а = μ₀μ = 4π10^-7100 = 1256,63710^-7 Гн/м

- на поверхности трубы.

По графику находим, это значение будет во всех последующих расчётах для частоты f.

1.1. При r=0 (В центре проводника).

1.2. При r=0,25R.

Далее всё считается по аналогии, для простоты восприятия запишем результаты расчётов в таблицу.

r	0	0,25R	0,5R	0,75R	R
r, м	0	0,00075	0,0015	0,00225	0,003
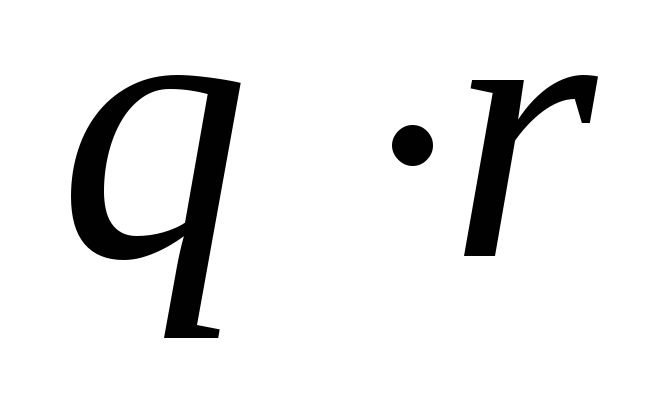
	0	1,82510025	3,6502005	5,475301	7,300401
	1	1,2600018	2,8800041	8,6400123	27,5400392
	0	0,9000013	2,7000038	8,1000115	26,2800374
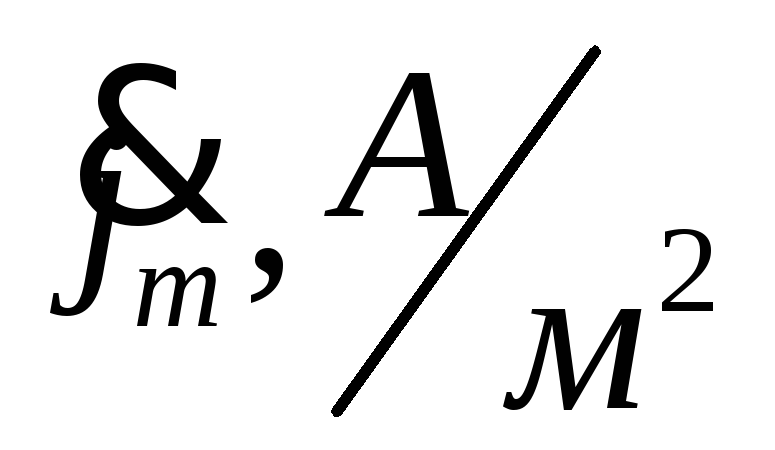
	12108,8763	15257,2059	34873,6134	104620,84	333478,928
	0	4,478386	13,435157	40,305473	137,934284

2. Определим плотность тока и напряженность магнитного поля внутри проводника при .

ω = 2πf = 23,142600 = 16336,28 рад/с

μ_а = μ₀μ = 4π10^-7100 = 1256,63710^-7 Гн/м

- на поверхности трубы.

По графику находим9325245,8487, это значение будет во всех последующих расчётах для частоты f.

2.1. При r=0 (В центре проводника).

2.2. При r=0,25R.

Далее всё считается по аналогии, для простоты восприятия запишем результаты расчётов в таблицу.

r	r	0,25R	0,5R	0,75R	R
r, м	0	0,00075	0,0015	0,00225	0,003
	0	6,5804925	13,160985	19,7414775	26,32197
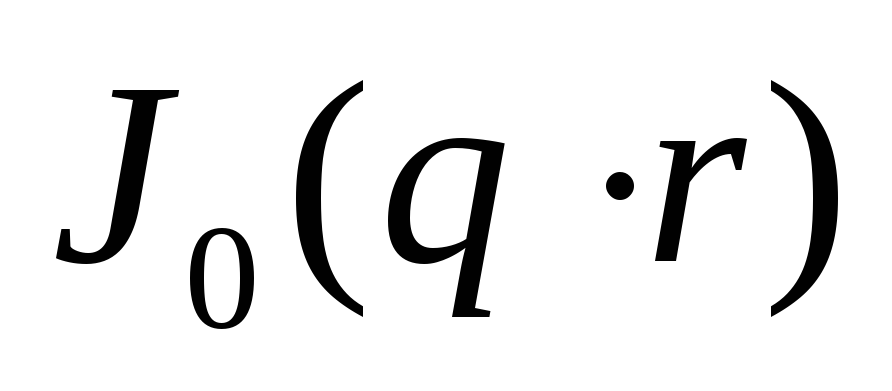
	1	16,532669	1218,464607	104141,2812	9451255,9299
	0	15,679492	1186,265673	102295,17818	9325245,8487
			158,132809
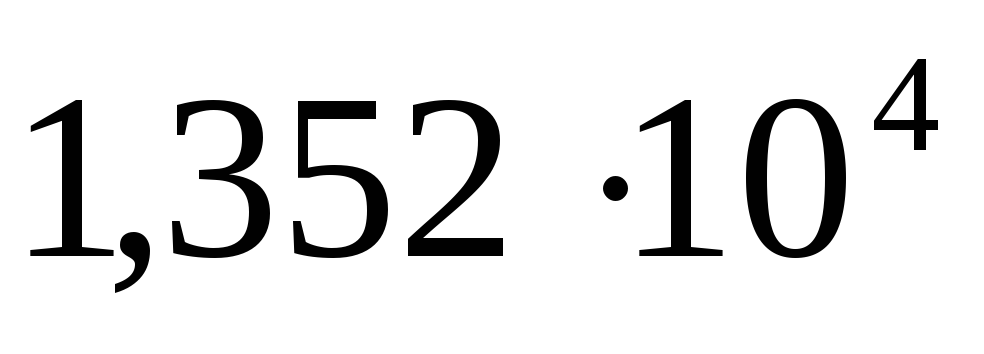
	0		0.017547	1,513098	137,934284

Рис.2.2. График зависимости модуля плотности тока магнитного поля от r.

Рис.2.3. График зависимости модуля напряженности магнитного поля от r.

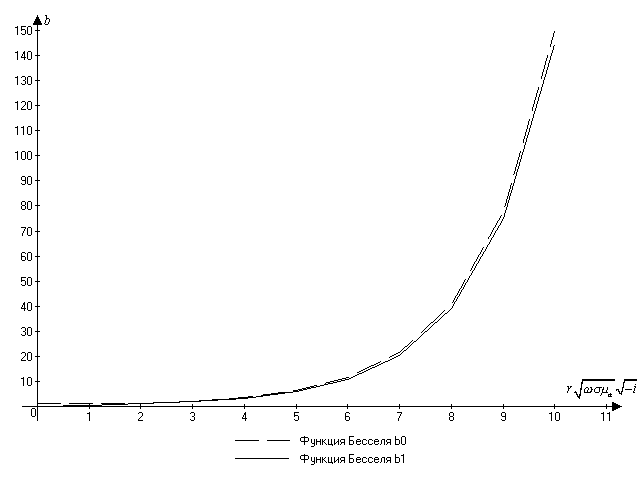
Рис.2.4. График для определения модулей функции Бесселя (b₀, b₁).

В следствии того, что аргумент функций Бесселя превышал 10, я использовала математический пакет Mathcad для определения значений функций Бесселя.

Выводы:

• При увеличении частоты f, магнитное и электрическое поля вытесняются от центра к стенкам цилиндрического провода (“поверхностный эффект”).

• При увеличении r от 0 до R, j_m увеличивается в ‘b₀’ раз.

• При увеличении r от 0 до R, H_m увеличивается в ‘b₁’ раз.

Часть № 3.

Исходные данные:

l=dl=10см=0,1м; Im=105 А; R=900 м; RА=0,32 м; А=320 град; RВ=250 м; В=315 град.

Длина отрезка прямолинейного провода; Амплитудное значение синусоидального тока; Радиус сферы; Координаты точки А в сферической системе координат; Координаты точки B в сферической системе координат.

По отрезку прямолинейного провода длиной l проходит переменный ток i = I_msin10⁸t, A. Среда, окружающая провод, - воздух. Считать, что со средней точкой отрезка провода совмещено начало отсчета сферической системы координат и что ось отсчета углов совпадает с положительным направлением тока в проводе.

Требуется:

1. построить полярную диаграмму зависимости от угла  модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R.

2. записать выражения для мгновенных значений векторов напряженности электрического и магнитного полей в точках А и В, предварительно выяснив, в какой зоне поля находится каждая точка. Радиус R, координаты точек А и В в сферической системе координат приведены в таблице.

Решение:

1. Построим полярную диаграмму зависимости от угла  модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R.

Ток i = I_msin10⁸t, A → ω=10⁸;

Оценим дальность точек находящихся на сфере (Расстояние R).

, значит точки лежат в дальней зоне( превышение R должно быть минимум в 6 раз).

Тогда

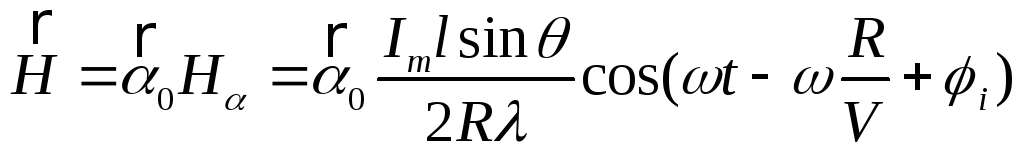, среднее значение равно:

, среднее значение равно:

Для воздуха .

Диаграмму зависимости векторов Е и Н в дальней зоне от угла θ называют диаграммой направленности.

Рис.3.1. Диаграмма направленности.

Выражение вектора Пойнтинга для дальней зоны:

Модуль вектора Пойнтинга (мгновенное значение):

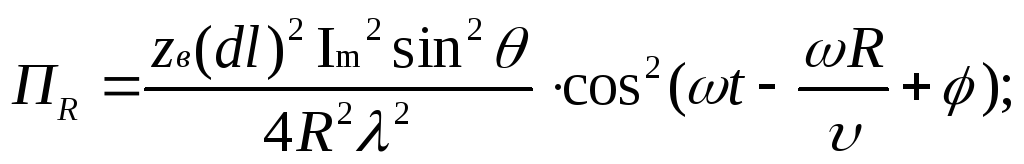
. Вектор Пойнтинга направлен по радиусу, а среднее значение его модуля за период :

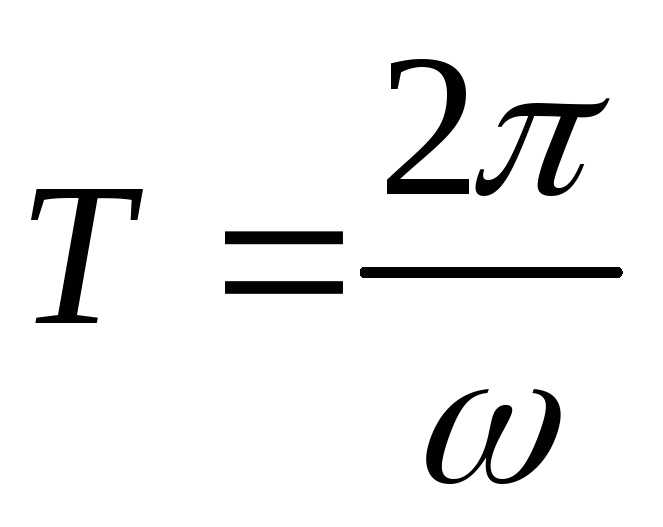т.к.

По этой функции построим полярную диаграмму зависимости от угла  модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R.

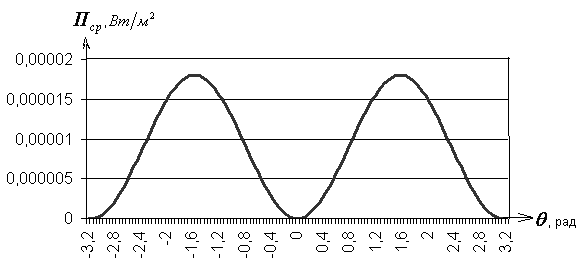
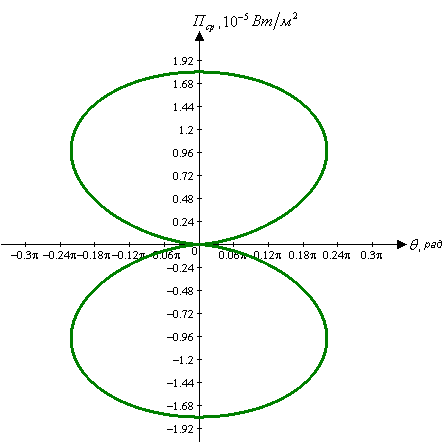
Рис.3.2. Полярная диаграмма зависимости от угла  модуля среднего за период значения вектора Пойнтинга в точках сферы радиусом R.

2. Запишем выражения для мгновенных значений векторов напряженности электрического и магнитного полей в точках А и В, предварительно выяснив, в какой зоне поля находится каждая точка.

Ток i = I_msin10⁸t, A → ω=10⁸;

Оценим дальность точек A и B.

2.1. Точка А (R_А=0,32м).

- значит точка A находится в ближней зоне.

В этом случае в компонентах электромагнитного поля мы пренебрегаем слагаемыми наименьшего порядка.

Мгновенные значения напряжённости электрического ( и ) и магнитного () поля вычисляем исходя из формул.

;

;

;

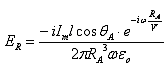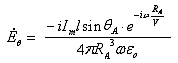Мгновенные значения:

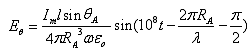
2.2. Точка B (R_B=250м).

- значит точка В находится в дальней зоне.

Мгновенные значения напряжённости электрического () и магнитного () поля вычисляем исходя из формул.

;

;

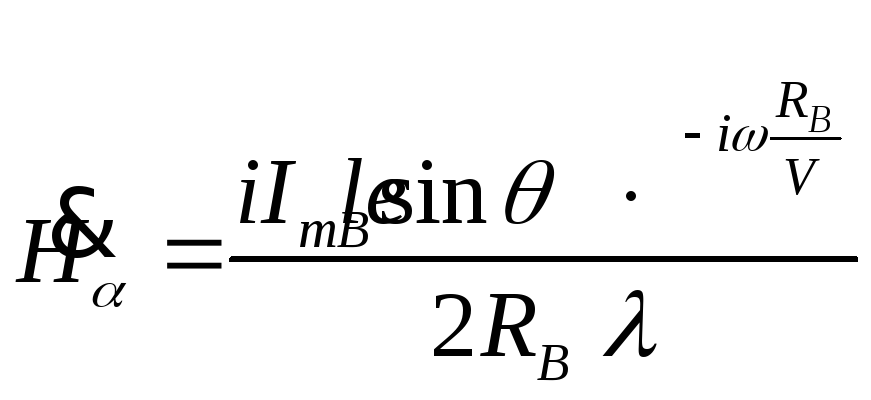Мгновенные значения:

Для воздуха волновое сопротивление будет иметь вид: .

.

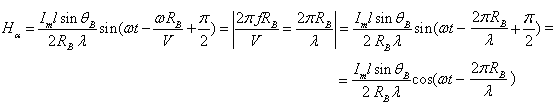
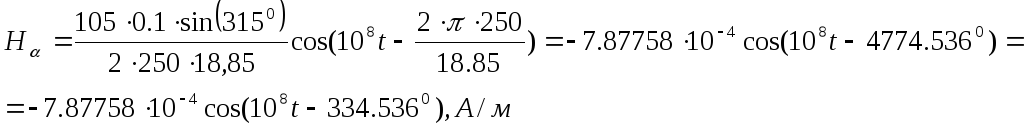
Выводы:

- Полярная диаграмма зависимости среднего за период значения вектора Пойнтинга от угла  в точках сферы представляет собой синусоиду с периодом .

- В зависимости от того, в какой зоне находится точка-ближней, дальней или средней-,

в компонентах электромагнитного поля мы пренебрегаем слагаемыми с наименьшим порядком, с наивысшим или не можем пренебречь ни одним соответственно. Если точка находится в дальней зоне, то мы также пренебрегаем составляющей E_r по сравнению с E_θ.

20