Средняя квадратическая

= ;

=

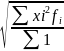
Средняягеометрическая, применяется только при расчетах средних коэффициентов роста или снижения.

=

n-число сомножителей под корнем.

=

n- число уровня ряда -1,получим число роста.

Например:

В течение рабочей недели (5) банк выдал ряд кредитов. Определить средний недельный темп роста выданных кредитов.

Дни недели	Сумма выданных кредитов .в 1000р.	Коэффициент роста или снижения
Пн	5858.0	-
Втр	5970	R1 = =1,019
Ср	6010	R2 = =1,0067
чтв	6100	R3 = =1,0150
пт	6150	R4 = =1,008

= =1,0122(101,22%)

Является частным случаем.

= ;

Средняя не взвешенная степенная

=

m-показатель степени определяющий вид ф.

x-варианты

f-веса при m=1 ,вычисляется формула арифметическая

при m-1-ср. гармоническая

m=0-ср. геометрическая

m=2-ср. квадратическая

Средние обладают св-ом можератности(св-ом не равности ),чем больше степень ,тем больше средняя.

Структурные средние (описательные)к ним относятся мода и медиана.

Мода –это наиболее часто встречающиеся значения признака в изучаемой совокупности.

Например:

Имеются данные, расположенные в порядке возрастания , о средней заработной плате рабочей бригады.

16.120,16120,16.120,16.140,16185,16215,16250.

Мода =16120 –часто встречается.

Медианой, называется значение признака находящееся в центре ранжиренного ряда и делящего этот ряд на две равные части по численности входящих в него единиц совокупности. Для определения места медианы в ранжиреванном ряду,вычисляется ее номер по формуле:

= = =4

Рассчитанная для данного ряда средняя равняется 16164,29, следовательно 4/7=0.57

Имеют з.п ниже средней.

При четном числе членов ряда также первоначально определяется номер медианы, а затем медиана будет равняться 16120+16140/2=16130

Расчет медианы в ряду распределения

Например:

Имеются данные о распределении группы студентов по росту .Определить среднюю моду и медиану.

Рост студентов в см. х	Числстуд	Произведение хifi	Накопленные частотыs- послед просуммчастоты
160	2	320
162	3	486
170	8	1360	13
190	6	1080	19
	2	380	21
итог	21	3626

= = =172,67 см

M₀ =170 см

Для нахождения медианы рассчитываем номер медианы.

N_Me= = =11

По номеру медианы и накопленным частотам находим медианное значение роста.

М=170см

Расчет модули медианы в интервальном ряду распределения

Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле:

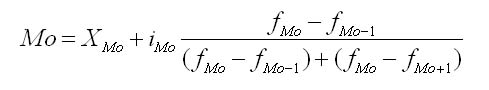
где Х_Мо— нижняя граница модального интервала; i_mo — модальный интервал; f_м0, f_м0-1,, f_м0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах. Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д.

В рядах с не равными интервалами

M₀ = x₀+i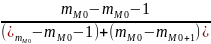

абсолютная плоскость распределения.

- относительная плоскость распределения.

𝟂-частость

i-плоскость интервалов

m_{M0 –} следующая за модальным

Медиана в интервальном ряду

Me=x₀ +i

x₀ -нижняя граница медианного интервала

i-шаг интервала

-номер медианы

- накопленные частоты предшествующие медианному интервалу

- частота медианного интервала