33.Числовая последовательность. Предепредел последовательности.

Числовой последовательностью называется числовая функция натурального аргумента:

X_n=f(n), определённая на множестве всех натуральных чисел, т.е. nN.

Задать числовую последовательность – значит задать правило, по которому каждому натуральному числу n соответствует одно и только одно число. В общем случае бесконечная числовая последовательность записывается в виде:

х₁, х₂, х₃,…….,х_n ,…….

(обозначают (х_n) или х_n, где nN). При этом х_n называется n-м членом или общим членом последовательности (х₁ – первый член последовательности, х₂ - второй и т.д.

Способы задания последовательности:

1. Аналитический – с помощью формулы n-го члена последовательности, по которой могут быть вычислены все остальные.

Например, пусть х_n=(-1)ⁿ/2n-1. Придавая n значения 1,2,3,4……, получаем развернутую запись этой последовательности:

-1, 1/3, -1/5, 1/7,…., (-1)ⁿ/2n-1,….;

2) табличный – каждому nN ставят в соответствие определённое числовое значение, что оформляют в виде таблицы;

3) рекуррентный – указывает несколько первых членов последовательности и правило (или формулу), позволяющее найти все последующие члены, использую предыдущие.

Например, пусть х₁=1, х₂=1 и каждый следующий член равен сумме двух предыдущих.

Получаем последовательность чисел 1,1,2,3,5,8,13,21……., называется числами Фибоначчи.

4) словесный – последовательность задают описательно (словами).

Предепредел последовательности

Число а называется пределом последовательности (х_n), если для любого >0 существует такое число n() что для всех n> n() выполняется:

х_n-a<0.

Пишут: lim _(x) x_n=a

Выполнение неравенства геометрически означает, что в случае существования предела все члены последовательности с номерами n> n() содержатся внутри интервала (а-, а+).

Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

36.Бесконечно малые величины и их св-ва

Опр. Функция f(x) называется бесконечно малой при ха, где а может быть числом или одной из величин , + или -, если .Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.Пример. Функция f(x) = xⁿ является бесконечно малой при х0 и не является бесконечно малой при х1, т.к. 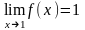.Теорема. Для того, чтобы функция f(x) при ха имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + (x),где (х) – бесконечно малая при х  а ((х)0 при х  а).

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах

.Доказательство теоремы 2. Представим f(x) = A + (x), g(x) = B + (x), где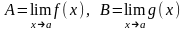 , тогдаf(x)  g(x) = (A + B) + (x) + (x)

A + B = const, (х) + (х) – бесконечно малая, значит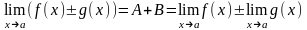

Теорема доказана.Доказательство теоремы 3. Представим f(x) = A + (x), g(x) = B + (x), где , тогда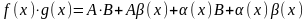

AB = const, (х) и (х) – бесконечно малые, значит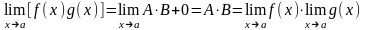 Теорема доказана.

38. 1 замечательный предел.

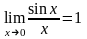
Возьмем круг радиуса 1, обозначим

радианную меру угла MOB через Х.

Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда

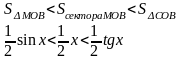
Разделим все на 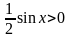и получим:

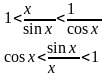
Т.к. 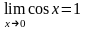, то по признаку существования пределов следует .

39.2 замечательный предел.

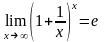
Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:

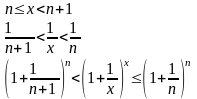
Если x→∞, то n→∞, тогда

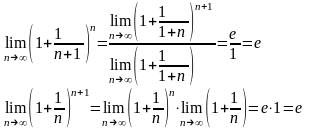
По признаку о существовании пределов:

40. Сравнение бесконечно малых.

Пусть при х  а а(х) и в(х) – бесконечно малые, тогда:

• если lim (в/а) = 0, то в – бесконечно малая высш. порядка, чем а.

• если lim (в/аⁿ) ≠ 0, то в – бесконечно малая n-порядка, чем а.

если lim (в/а) = 1, то а и в – эквивалентные бесконечно малые.

41. Непрерывные функции и их свойства. Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке:

Это означает:

- функция определена в точке х₀ и в ее окрестности;

- функция имеет предел при х→х₀

- предел функции в точке х₀ равен значению функции в этой точке, т.е. выполняется равенство.

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х₀

42.Точка разрыва функций и их классификация.

Точки разрыва функции – это точки в которых нарушается непрерывность функции.

Точка разрыва х₀ называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)

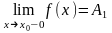и

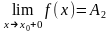
При этом, если:

- А₁=А₂ то точка х₀ называется точкой устранимого разрыва;

- А₁≠А₂ то точка х₀ называется точкой конечного разрыва.

|A₁ – A₂| называется скачком функции.

Точка разрыва х₀ называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.

43. Непрерывность функции в точке. Действия над непрерыв функциями

x=x₀+x, x=x-x₀

y=f(x₀+x)-f(x₀)

Ф-ция y=f(x) наз. непрерывной в точке x₀, если она определена в окрестности этой точки, а limy=0. (бесконеч.малая. приращению аргумента соответствует б.м. приращению ф-ции).

limy=lim[f(x)-f(x₀)]=limf(x)-limf(x₀)=0, то

limf(x)=limf(x₀)

xx₀

Ф-ция непрерывна в точке х₀, если ее предел = значению этой ф-ции в точке х₀

Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке.

44. Производная. Геометрический смысл.

1. _cp.=S/t, =lim(S/t), где t0

2. p_cp.=m/l, p_T=lim(m/l), где l0

y=f(x+x)-f(x), y=f(x)

lim(y/x)=lim((f(x+x)-f(x))/x)

x0 x0

Смысл производной - это скорость изменения ф-ции при изменении аргумента.

y=f(x+x)-f(x), y=f(x). производной в точке а называется предел отношения приращения ф-ции к приращению аргумента:

lim(y/x)=lim((f(x+x)-f(x))/x)=dy/dx

x0 x0

Вычисление производной: lim(y/x)=y` x0

1) если y=x, y=x, y`=x=lim(y/x)=1.

2) если y=x², y=(x+x)²-x²=x²+2xx+x²-x²=x(2x-x),

(x²)`=lim((x(2x+x))/x)=lim(2x+x)=2x

x0 x0

Геометрический смысл производной.

K N=y, MK=x

MNK/tg2=y/x

вычислим предел левой и правой части:

limtg=lim(y/x) x0

tg₀=y`

₀

При x0 секущая MNзанять положение касательной в точке M(tg₀=y`, ₀)

Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x₀.

45. . Дифференциал ф-ции и его геометрический смысл. Св-ва дифференциала.

limy=A, y=A+

limy/x=y`, y/x=y`+, y=y`x+x

x0

y=y`x+, где -б.м.в., величина более высокого порядка малости,, чем x(), и ее можно отбросить.

dy=y`x

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента х и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем х.

Если y=x, то dy=dx=x`x=x, dx=x

Если yx, то dy=y`dx, y`=dy,dx

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину x

Св-ва: 1. (UV)`=U`V`, то (UV)`dx=U`dxV`dx, d(UV)=d(UV)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².