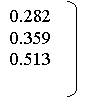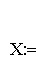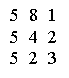Лабораторная работа № 4 Вычисление сумм и произведений. Символьные вычисления. Операции с комплексными числами
Цель: Научиться вычислять суммы и произведения элементов множеств в цифровом и символьном виде, выполнять операции с комплексными числами.
Ход работы
1.
Для вычисления
сумм и произведений воспользуемся
панелью Исчислений
на
панели инструментов математика.
Например:
вычислим суммы следующих рядов:
=
1.635
=
1.543
=
0.5
Для
этого используется значок суммы
с
указанием границ суммирования.
Из
примеров видно, что система обрабатывает
ситуации (-1)0
=
1 0! = 1. Но, к сожалению, не может
считать суммы с бесконечными пределами.
В случаях, когда пределы изменения
индекса указываются в виде переменной
интервального типа (например, для работы
с матрицами и функциями, зависящими от
индекса) используется знак суммирования
только с указанием индекса
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например: вычислим сумму элементов матрицы:
i:=0..2
=
1.154
2. Вычислите сумму элементов матрицы своего варианта.
3. Аналогично вычисляются произведения.
|
|
|
|
По
определению:
Например:
вычислим произведение элементов
следующих рядов:
=
0.5
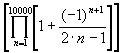=1.414
х: = 0.5
=
2
4.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||
Вычислим
сумму и произведение диагональных
элементов для матрицы
i: = 0…2
=
12
=60
5. Суммы и произведения можно вычислить в символьном виде.
Например:
или
по конечному пределу
.
Здесь
появляется функция
,
определение которой можно найти в меню
Справка .
Вычислите
также следующие суммы:
+
Получаем просто ряд из 8 слагаемых, это значит, что система не смогла упростить выражение. Аналогично попытаемся вычислить произведение:
6. Mathcad предусматривает работу с комплексными числами. Комплексные числа вводятся в обычной алгебраической записи, в качестве мнимой единицы используется символ i или j.
Внимание! Для ввода комплексной единицы единице необходимо напечатать “1i” или “1j”.
Введем два комплексных числа:
a:= 2 + 3i b:= -1 + 4j
Выполним с ними различными операциями.
Сложение: с:= а + b с = 1+7i
Вычитание: с:= а – b с = 3 – i
Умножение: a ∙ b = -14 + 5i
Деление:
=
0.588 – 0.647i
Комплексные
сопряжения:
=
2 - 3i
=
-1 – 4i
Комплексное сопряжение выводится символом двойной кавычки после набора имени переменной (“).
В случае многозначности корней система возвращает корень с наименьшей мнимой частью.
ei
= 0.54 + 0.84i
sin (i) =
1.175i
cos (i) = 1.543
=
i
=
-1
=
0.866 + 0.5i
Для работы с комплексными числами используются следующие функции:
Re (z) – действительная часть числа
Im (z) – множественная часть числа
arg (z) – аргумент (угол в комплексной плоскости между вещественной осью и осью Z)
–
модуль
В нашем случае:
Re
(
)
= 2
Im (
)
= 3
=
3.606 arg (
)
= 0.983
Re
(
)
= 2
Im (
)
= -3
=
3.606 arg (
)
= -0.983
7. Выполните индивидуальное задание.
8. Покажите результат преподавателю.