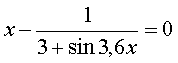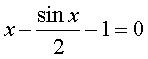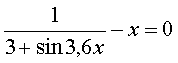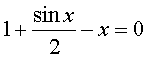Лабораторная работа №3 Решение уравнений и систем уравнений

Цель: научиться решать квадратные уравнения, уравнения с одной производной, а также системы и нелинейных уравнений, используя возможности программы Mathcad.

Ход работы

1.        Решение квадратного уравнения. Программа Mathcad позволяет находить корни многочлена второй степени         . Введем коэффициенты  а:=1    b:=-2    с:=-8. И определим функцию:                                                   Переменной  присваиваем значение:                                                          Переменной  присвоим значение функции                                                    Получаем корни:    .

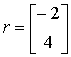2.        Решение уравнения с одной неизвестной.     Используя возможности программы Mathcad, можно найти корни уравнения  для заданной функции     Определим функцию:                                      Зададим начальное приближение для поиска корня. Если уравнение имеет несколько корней, для поиска нового корня следует задавать новое начальное приближение. Для поиска комплексных корней следует задавать комплексное начальное приближение:                                                   х:=1 Получаем искомое решение:                                      soln                   soln Иногда алгоритм поиска корня натыкается на локальный минимум функции, при этом появляется сообщение “отсутствие сходимости” (испытайте на данном примере начальное приближение х=10). В таком случае следует попробовать другое начальное решение.

3.        Решение систем линейного уравнения.     Системы линейных уравнений решаются матричным способом (см л/р№2)     Решите следующую систему:                                           

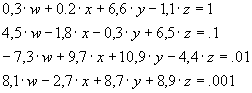
Вектор искомых решений:      soln .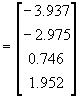

4. Решение систем нелинейных уравнений. Используя блок решения уравнений, Mathcad находит решение системы n нелинейных уравнений с n неизвестными. 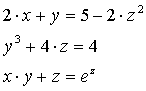Зададим начальные приближения для всех неизвестных:                 х:=1              у:=1                z:=0 Вводим уравнения в блок решения уравнений: Given                                                                                          -начало блока                                                                                                                               -конец блока Найденное решение:

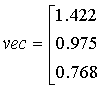
5. Выполните индивидуальное задание.

6. Показать результат преподавателю.

 

Варианты заданий

Задание для всех вариантов.

1.Решить систему линейных уравнений матричным способом.

x₁+5x₂+x₃=V+12

3x₁-x₂+x₃=V-1

Vx₁+3x₂+(V+4)x₃=V(V+2)-6

Здесь V – номер компьютера.

 

2.Решить уравнение с одной неизвестной.

1.		Начальное приближение 0
2.		Начальное приближение 1
3.		Начальное приближение 0
4.		Начальное приближение 0
5.		Начальное приближение 0
6.		Начальное приближение 0
7.		Начальное приближение 1
8.		Начальное приближение 0
9.		Начальное приближение 0
10.		Начальное приближение 1
11.		Начальное приближение 0
12.		Начальное приближение 0