Лекция 14. Степенные ряды. Радиус сходимости ряда. Разложение функций в ряд Тейлора, ряд Маклорена. Применение степенных рядов для приближенного вычисления значений функций и интегралов.
Определение
Степенным рядом называется функциональный ряд
,
элементы которого произведения постоянных
на степенные функции с целыми
показателями степеней от разности
-
коэффициенты степенного ряда (обычно
действительные функции).
В частности, если
,то
мы будем иметь степенной ряд, расположенный
по степеням x
В дальнейшем рассматриваем именно такие
ряды (замена
)
Для удобства n-м элементом
степенного ряда называют элемент
(хотя он стоит на n+1 месте).
Свободный элемент
считается
нулевым элементом ряда.
Рассмотрим ряд
(*)
и докажем очень важную теорему, на которой будет основано изучение таких рядов.
Теорема Абеля
Если степенной ряд (*) сходится в точке
,
то он сходится и притом абсолютно, в
интервале
,
т. е. при всяком x ,
удовлетворяющем условию
.
Доказательство:
Заметим, что вследствие сходимости ряда
его
общий элемент
.
Поэтому все элементы этого ряда ограничены
в совокупности, т.е. существует М>0,
такое, что при всяком n
.
Запишем ряд (*) так
и составим ряд их абсолютных величин
элементов этого ряда:
В силу установленного неравенства
каждый элемент здесь меньше соответствующего
элемента геометрической прогрессии со
знаменателем
:
Если
,
то
и прогрессия сходится, поэтому сходится
ряд из абсолютных величин, а значит,
абсолютно сходится сам ряд (*). Теорема
доказана.
Несмотря на то, что
нельзя сразу воспользоваться признаком
сравнения, поскольку в условиях теоремы
не сказано, что ряд в самой точке
сходится абсолютно.
Следствие
Если степенной ряд (*) расходится при
, то он расходится и при всяком х,
большем по абсолютной величине
,
то есть при
Область сходимости степенного ряда
Здесь возможны три случая:
Область сходимости состоит только из одной точки х=0, то есть ряд расходится для всех значений х, кроме х=0. Пример
Если х фиксировано и х не равно
0,то, начиная с достаточно большого n,
будет
,
откуда вытекает неравенство
,
означающее, что общий элемент ряда не
стремится к нулю.
Область сходимости состоит из всех точек оси ОХ, то есть ряд сходится при всех значениях х. Пример
Для любого х, начиная с достаточно
большого n, будет
,
так как
и т.д.
Начиная с номера n, элементы ряда по абсолютной величине будут меньше элементов сходящейся геометрической прогрессии. Следовательно, при любом х ряд сходится.
Область сходимости состоит более чем из одной точки оси ОХ, причем есть точки оси, не принадлежащие области сходимости. Пример
Это геометрическая прогрессия со
знаменателем х. Ряд сходится при
|x|<1 и расходится
при
.
В этом случае на числовой оси наряду с точками сходимости ряда имеются и точки его расходимости.
Из теоремы Абеля и ее следствия вытекает, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.
Таким образом
Для каждого степенного ряда, имеющего
как точки сходимости , так и точки
расходимости, существует такое
положительное число R,
что для всех х по модулю меньшим R
(
),
ряд абсолютно сходится, а для всех |x|>R
ряд расходится. При x=R
и x=-R различные
варианты:
А) ряд сходится в обеих точках.
Б) ряд сходится в одной из точек.
В) ряд расходится в обеих точках.
Определение
Радиусом сходимости степенного ряда (*) называется такое число R, что для любых х, |x|<R, степенной ряд сходится, а для всех х, |x|>R, расходится. Интервал (-R,R) называется интервалом сходимости.
Считаем, что если ряд расходится для любого х, кроме х=0, R=0.
Если ряд сходится при всех х, то
считаем
или
.
Для ряда
центр интервала сходимости в точке
( а не х=0) и интервал сходимости
.
Способ отыскания радиуса сходимости степенного ряда
Отметим, что для нахождения радиуса сходимости можно исследовать ряд, составленный из абсолютных величин элементов исходного ряда, то есть
(**) так как интервалы сходимости ряда
(*) и ряда (**) совпадают. К ряду (**) применим
признак Даламбера.
будет
содержать |x| или
степень |x|
Для тех значений х, при которых получаемый предел меньше 1, ряд сходится, а для тех, при которых x>1, ряд расходится. Отсюда следует, что значения |x|, при которых этот предел равен 1, и будет являться радиусом сходимости ряда.
Может случиться, что найденный предел при всех х будет равен 0. Это означает, что ряд (*) сходится при всех х и .
Наоборот, если для любых х кроме х=0 предел равен бесконечности, то ряд будет везде расходиться, кроме х=0, то есть R=0.
Примеры
Найти радиус сходимости ряда
,
то есть для всякого х ряд сходится
.
Найти радиус сходимости ряда
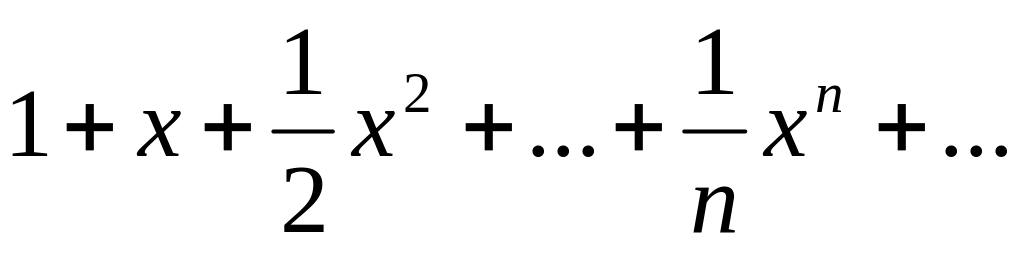
Если |x|<1 - ряд сходится
Если |x|>1 – ряд расходится
При х=1 получаем гармонический ряд, который расходится.
При х=-1 ряд
сходится условно.
Найти радиус сходимости ряда
,
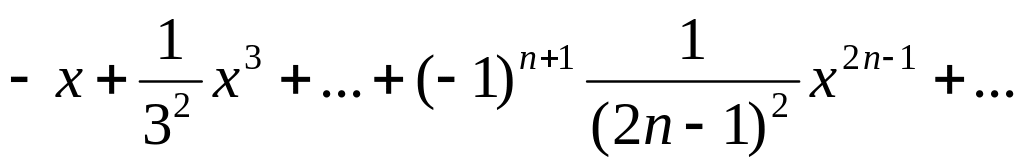
то есть R=1
При |x|<1 – ряд сходится
При |x|>1 – ряд расходится
При |x|=1 – ряд сходится абсолютно.
Найти радиус сходимости ряда
Если
ряд сходится, то есть при -2<x-1<2.
Получаем интервал сходимости (-1,3)
с центром х=1.