1. Выбор и обоснование методов решения

   1. Понятие машинного и реального времени

Реализацию любой программы можно проводить по двум путям: либо в темпе быстродействия ЭВМ (с учётом быстродействия языка программирования), либо в реальном масштабе времени. При этом время задержки напрямую зависит от частоты процессора, и эта программа может наиболее объективно использоваться на той ЭВМ, для которой она была написана. Машинное время является относительным, т.к. зависит от быстродействия ЭВМ, от используемого языка, от сложности алгоритма и т.д.

Исследователь должен уметь связывать последовательность результатов с реальным временем, проводить эксперимент в реальном времени. Моделирование в реальном времени дает возможность оценивать эффективность алгоритмов для работы в реальных системах.

2. Дискретизация времени

При исследовании блоков и систем во временной области на ЭВМ, в частности микроЭВМ, непрерывные процессы заменяются на дискретные. При этом временной интервал L представляется как совокупность дискретных интервалов:

,

где T_k – период квантования по времени непрерывной функции;

n – количество шагов или квантов.

Количество квантов выбирается не произвольно, а исходя из максимальной частоты процесса и допустимой погрешности при моделировании.

3. Реализация временных задержек в программе

Можно выделить два основных способа реализации временных задержек в программе. Первый – самый простой – состоит в том, чтобы прямо указать программе, сделать паузу (например, оператором DELAY). Второй способ – организовать цикл, внутри которого выполняется арифметическая операция, абсолютно не влияющая на результат выполнения программы.

4. Метод Крамера для решения системы линейных уравнений

Система линейных уравнений:

a ₁x + b₁x₂= c₁

a₂x + b₂x₂ = c₂ ,

Имеет одно решение (x₁, x₂), если система является невырожденной т.е. выполняется неравенство:

a₁b₂-a₂b₁≠0,

Тогда решение можно найти по общим формулам:

5. Метод Ньютона

Задано: , и . При использовании этого метода нелинейное уравнение должно быть приведено к виду .

Введем обозначения: - левая часть нелинейного уравнения; – первая производная от ; .

Так как вычисления искомого значения производится в этом методе иначе, чем в методе простой итерации, то значения могут использоваться без индексов. Анализ нахождения искомого значения можно упростить. Это несложное доказательство оставляется студентам.

Итак, алгоритм решения:

1. Задаем значение _.

2. Вычисляется .

3. Вычисляется .

4. Определяется .

5. Вычисляется .

6. Проверяется условие _.

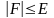Если условие выполняется, то - искомый корень, в противном случае следует повторить цикл с п.2.

6. Алгоритм (схема) Горнера

Известно, что полином в общем виде записывается следующим образом:

_.

Горнер предложил переиндексировать коэффициенты многочлена:

_.

Далее он предложил разложить многочлен и представить в виде:

_.

Исходя из такого представления, он предложил алгоритм, который еще называют схемой Горнера:

-все коэффициенты представить в виде элементов массива;

-должны учитываться все коэффициенты. Если они отсутствуют в полиноме, то их надо все равно использовать, считая их равными нулю;

-до цикла FOR-NEXT взять значения y=A(1);

-цикл по управляющей переменной организовывать с I=2 до X+1;

-в цикле использовать формулу:

Y=Y*X+A(I).

Если все значения Y надо сохранить, то Y следует организовать тоже как массив.