3. Преобразование чисел из одной системы счисления в другую

В результате изучения данной темы Вы будете:

• знать основные правила, используемые для перевода чисел из одной системы счисления в другую;

• уметь использовать упрощенные правила при переводе чисел из двоичной системы счисления в восьмеричную или шестнадцатеричную (и обратно).

Вычислительные машины работают с двоичными кодами, а пользователю удобнее иметь дело с десятичными или шестнадцатеричными. Поэтому возникает необходимость перевода чисел из одной системы счисления в другую.

Преобразование числа Х из системы счисления с основанием q в систему счисления основанием р (преобразование Х_(q) → Х_(p)) осуществляется по правилу замещения или по правилу деления-умножения на основание системы счисления. Давайте подробней остановимся на этих правилах.

Правило замещения

Реализуется на основании формулы ( 1 .1) и предусматривает выполнение арифметических операций с кодами чисел в новой системе счисления. По­этому оно чаще всего используется для преобразования чисел из недесятичной системы счисления в десятичную.

Например, выполним преобразование Х₍₂₎ → Х₍₁₀₎, если Х₍₂₎ = 10101,011:

X₍₁₀₎ = 1•2⁴+0•2³+1•2²+0•2¹+l•2⁰+0•2^-l+l•2^-2+l•2^-3 = 21,375

Правило деления-умножения

Предусматривает выполнение арифметических опе­раций с кодами чисел в исходной системе счисления с основанием q, поэтому его удоб­но применять для преобразования десятичных чисел в любые другие позиционные сис­темы счисления. Правила преобразования целых чисел и правильных дробей различны. Для преобразования целых чисел используется правило деления, а для преобразования правильных дробей – правило умножения. Для преобразования смешанных чисел ис­пользуются оба правила соответственно для целой и дробной частей числа.

Правило деления

Используется для преобразования целого числа, записанного в q-ичной системе счисления, в р-ичную. В этом случае необходимо последовательно делить исходное q-ичное число и получаемые частные на новое основание р, пред­ставленное в p-ичной системе счисления. Деление продолжают до тех пор, пока оче­редное частное не станет меньше р. После замены полученных остатков и последнего частного цифрами ручной системы счисления записывается код числа в новой систе­ме счисления. При этом старшей цифрой является последнее частное, а следующие за ней цифры соответствуют остаткам, записанным в последовательности, обратной их получению.

Например, выполним преобразование Х₍₁₀₎ → Х₍₁₆₎, если Х₍₁₀₎ = 7038:

Для получения частных и остатков по правилу деления для целой части числа удоб­но использовать формулу записи, известную под названием «деление в столбик»:

Таким образом, из полученных остатков деления (14, 7, 11, 1, а используя основание 16: E, 7, B, 1) выводим число 1B7E₍₁₆₎.

Правило умножения

Используется для преобразования дробного числа, записанно­го в q-ичной системе счисления, в р-ичную. В этом случае необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание р, представленное в исходной q-ичной системе счисления. Целые числа получаемых произведений, замененные цифрами р-ичиой системы счисления и дают последователь­ность цифр в новой р-ичной системе.

Умножение необходимо производить до получения в искомом р-ичном коде циф­ры того разряда, вес которого меньше веса младшего разряда исходной q-ичной дроби. При этом в общем случае получается код приближенно, и всегда с недо­статком значения дроби. Поэтому в случае обратного преобразования (р-ичиого кода дроби в q-ичный) результат может не совпадать с исходным значением q-ичной дроби.

Например, выполним преобразование X₍₁₀₎ → X₍₂₎, если X₍₁₀₎ = 37,45.

Для целой части (37) используем правило деления, а для получения дробной части числа (0,45) – правило умножения. Применительно к рассматриваемому примеру имеем:

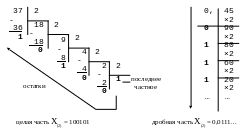
Таким образом, в результате преобразования получаем 37,45₍₁₀₎ = 100101,0111…₍₂₎.

Как следует из примера, процесс перевода дробной части можно продолжить до бесконечности. Однако, т.к. компьютеры оперирует числами конечной точности, дроби округляют в соответствии с правилами преобразования и весом младшего разряда исходной дроби.