Министерство образования и науки Российской Федерации

_______

САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

___________________________________________________________________________

А.И. Кириллов Е.М. Ротинян

МЕХАНИКА ЖИДКОСТИ И ГАЗА

ПЛОСКОЕ ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ

НЕСЖИМАЕМОЙ ЖИДКОСТИ:

ЦИРКУЛЯЦИОННОЕ ОБТЕКАНИЕ

КРУГЛОГО ЦИЛИНДРА

Учебное пособие

Санкт-Петербург

Издательство Политехнического университета

2005

ОГЛАВЛЕНИЕ

1. Потенциал скорости и функция тока 3

2. Связь циркуляции с положением критических точек 3

3. Построение линий тока 6

3.1. Основная линия тока 7

3.2. Верхние и нижние линии тока 10

4. Вычисление силы Жуковского 14

5. Распределение скорости и коэффициента давления

по поверхности цилиндра 14

6. Рекомендации по оформлению расчетного задания 15

Библиографический список 15

1. Потенциал скорости и функция тока

Картина потенциального течения, соответствующая циркуляционному обтеканию цилиндра, получается при наложении друг на друга трех простейших течений: плоскопараллельного однородного потока, диполя, расположенного в начале координат, и точечного вихря, также помещенного в начало координат.

Комплексный потенциал сложного течения, полученного наложением трех указанных течений, представляет собой алгебраическую сумму их комплексных потенциалов: – для однородного плоскопараллельного потока, направленного вдоль оси абсцисс (c_ - скорость потока); – для диполя (m – момент диполя) и – для точечного вихря (Г – циркуляция вектора скорости по контуру, охватывающему вихревую точку). Здесь – комплексная независимая переменная.

В результате получим

. (1)

Выделим в комплексном потенциале действительную и мнимую части. Для этого воспользуемся при преобразовании первого и второго слагаемых тригонометрической формой записи комплексного числа

(2)

где – модуль; – аргумент комплексного числа.

Во втором слагаемом комплексная независимая переменная – в знаменателе, поэтому сразу вычислим

(3)

Преобразуя третье слагаемое, запишем комплексное число в экспоненциальной форме . Тогда

(4)

После подстановки (2), (3) и (4) в (1) получим:

(5)

Момент диполя m в выражениях (1) и (5) может быть вычислен через известный радиус R цилиндра:

. (6)

В плоской постановке цилиндр вырождается в окружность, причем формулы (1) – (6) записаны для случая, когда центр окружности расположен в начале координат.

Как известно, комплексный потенциал содержит действительную и мнимую части:

, (7)

где  – потенциал скорости (действительная часть комплексного потенциала);  – функция тока (мнимая часть комплексного потенциала). Поскольку комплексные числа равны, когда раздельно равны их действительные и мнимые части, из выражений (5) и (7) следует:

, (8)

. (9)

Функция тока сохраняет постоянное значение на линии тока. Проверим, является ли окружность радиуса R линией тока. Для этого подставим r = R в выражение для функции тока (9):

(10)

Поскольку на окружности радиуса R значение функции тока оказалось постоянным, окружность, как и при обтекании цилиндра без циркуляции, является линией тока, и ее можно считать контуром кругового цилиндра.

2. Связь циркуляции с положением критических точек

Критическими точками называются точки разветвления линий тока. Поскольку вектор скорости в каждой точке линии тока направлен по касательной к ней, в критической точке скорость равна нулю. В противном случае вектор скорости в критической точке имел бы несколько направлений – по касательным к каждому участку линий тока, сходящихся в критической точке, что невозможно. Нулевой же вектор не имеет направления.

Для точек на поверхности цилиндра радиальная составляющая скорости отсутствует (поверхность цилиндра непроницаема для обтекающей жидкости). Кроме того, для критических точек и касательная (тангенциальная) составляющая скорости равна нулю. Выразим тангенциальную скорость через производную потенциала скорости по углу . Поскольку , то

На поверхности цилиндра (r = R) тангенциальная проекция скорости

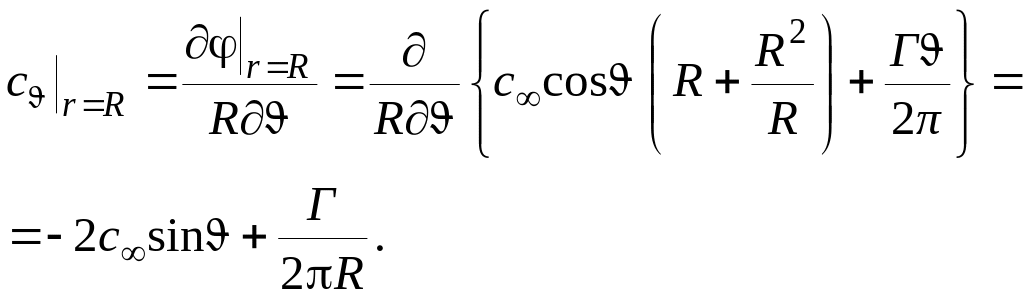(11)

В критических точках (при ) скорость . Поэтому

(12)

Чтобы критические точки располагались на поверхности цилиндра, в уравнении (12) справа от знака равенства должно стоять выражение меньше единицы. Тогда тригонометрическое уравнение имеет два вещественных корня (два значения критического угла), которые лежат в первом и втором квадранте при положительной циркуляции, либо в третьем и четвертом квадранте при отрицательной циркуляции.

Равенство (12) устанавливает связь между значением циркуляции и положением критических точек, что позволяет задавать для расчета любую из указанных величин.