3 Способ перехода от одного дбр к другому.

Сначала рассмотрим конкретный пример.

Пусть имеем ЗЛП:

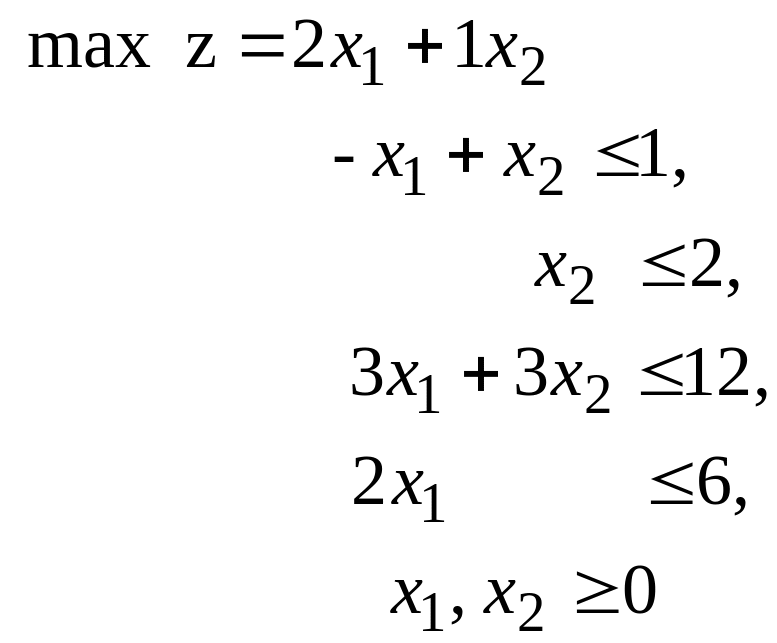
Приведем задачу к канонической форме

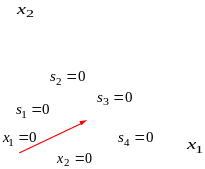
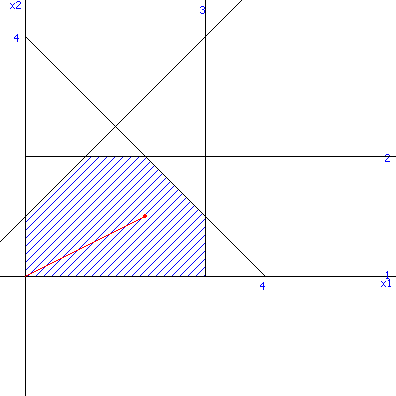
Нам необходимо найти какое-то ДБР. По определению ДБР:

• ß – совокупность линейно-независимых векторов;

• при ;

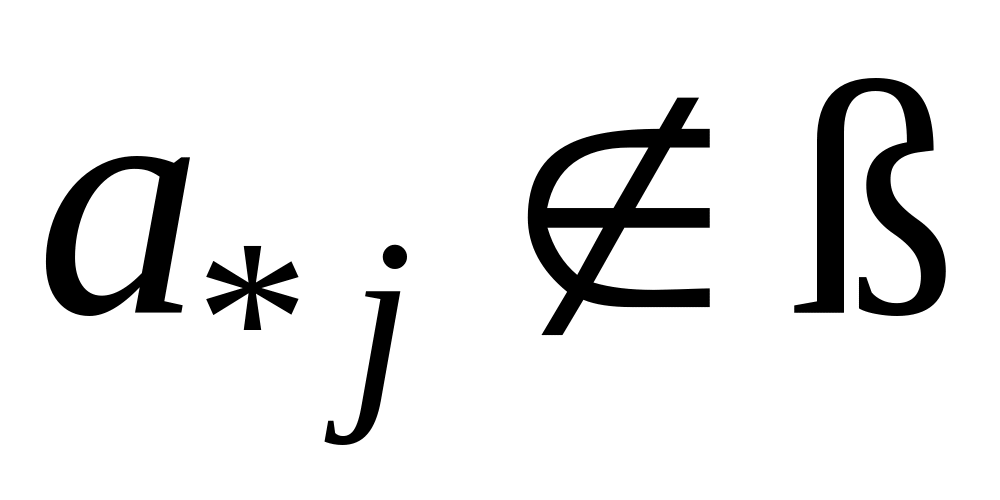• затем ;

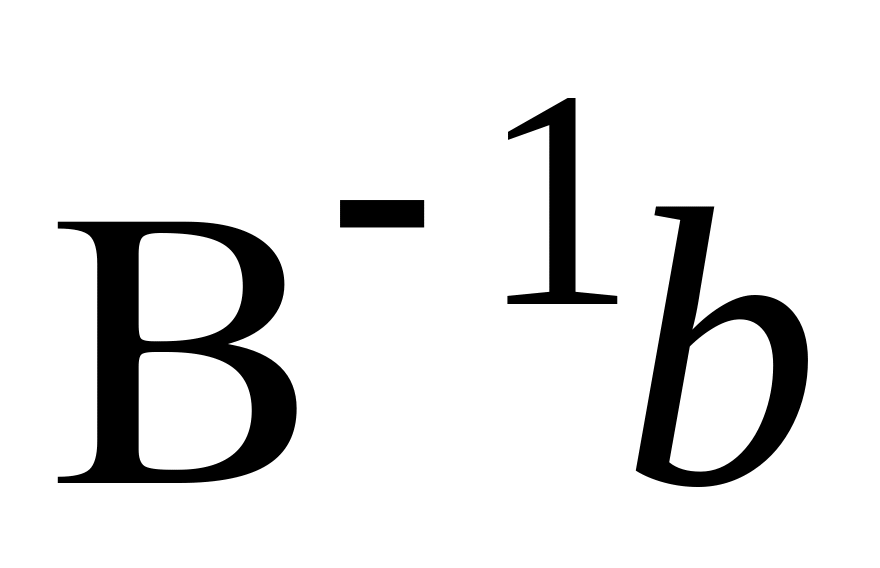• если 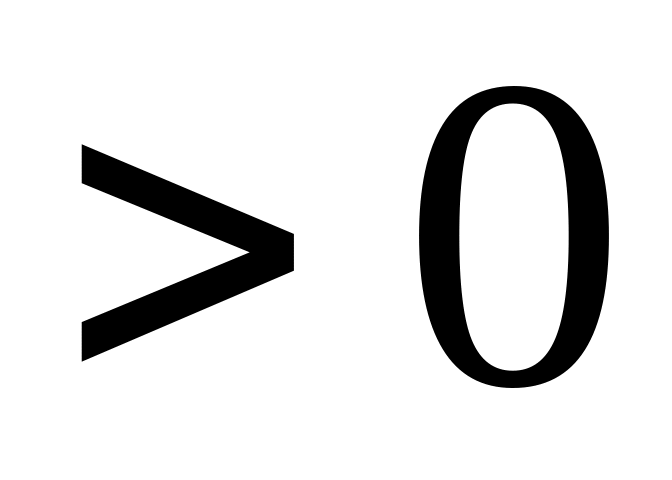, то имеем ДБР с 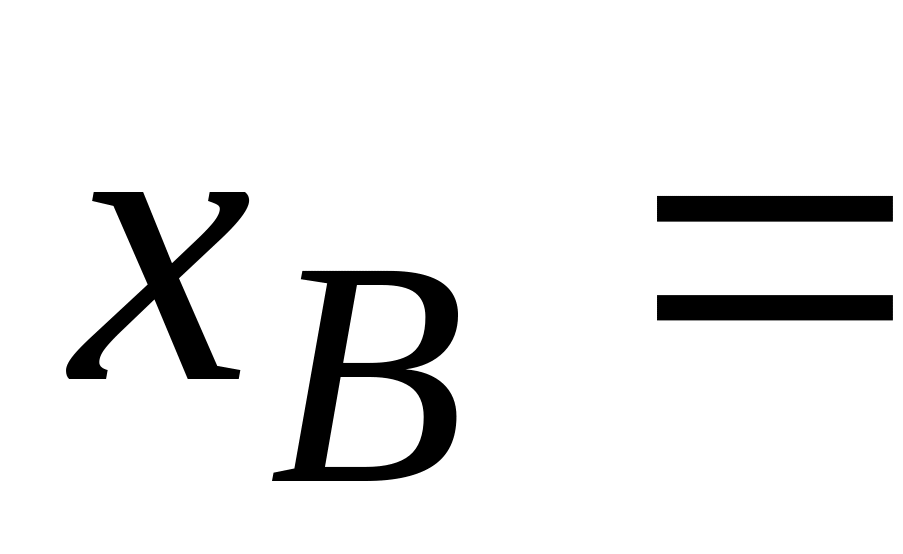, иначе (имеем недопустимое БР) – все нужно выполнить заново.

Таким образом, нужно найти базис, которому бы ответствовало ДБР. Мы видим, что система диагональная относительно переменных , и при этом правые части уравнений неотрицательны. Если принять в качестве базисных векторы, соответствующие этим переменным, то получим, что .

Точка 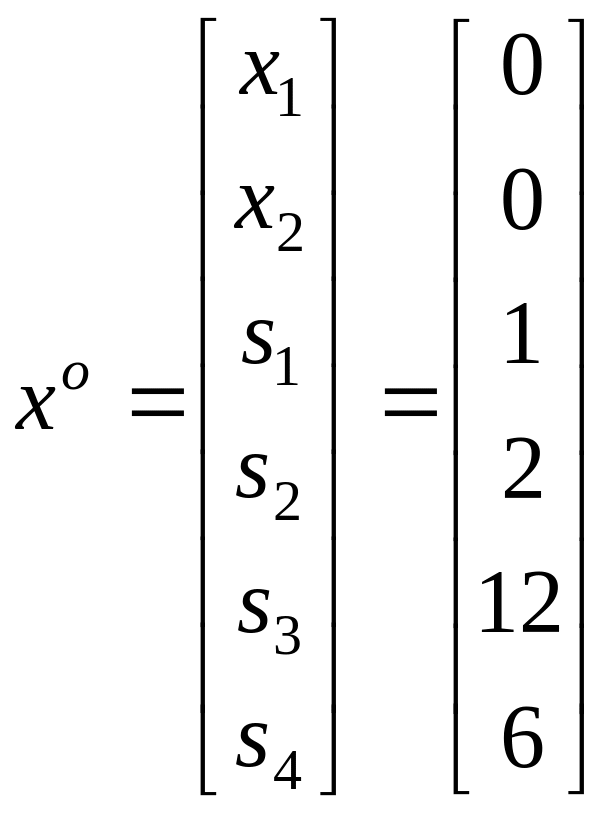є ДБР (йому відповідає точка початку координат – точка A)..

A B

Запишемо систему обмежень відповідної перетвореної задачі:

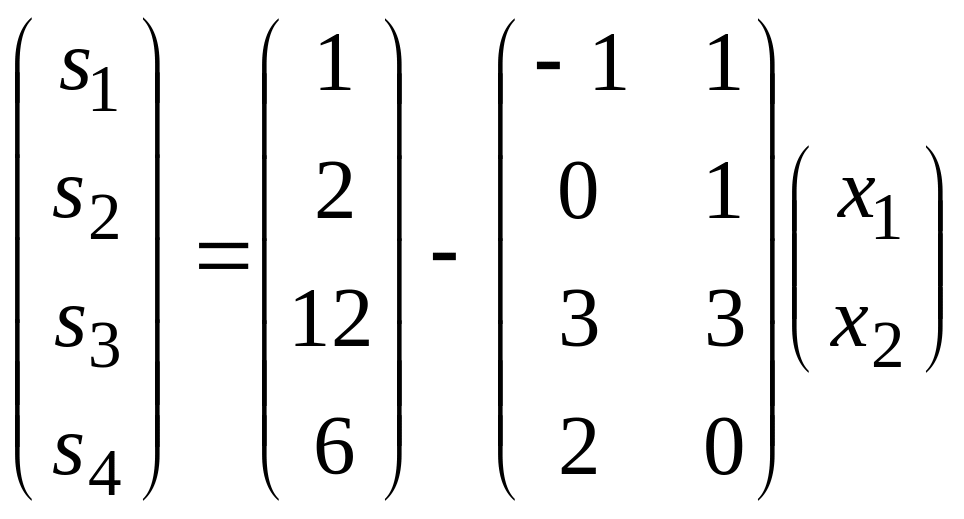
Нехай небазисна змінна почне зростати, приймаючи додатні значення, в той час, як інша небазисна змінна залишиться нульовою. Це означає, що ми починаємо рухатись по ребру AB. При збільшенні

• збільшується;

• не змінюється;

• зменшується;

• зменшується;

при цьому змінна першою обернеться в нуль (те, що буде відбуватися з відповідною базисною змінною, залежить від значення відповідної компоненти вектора ). Максимально допустиме значення збільшення становить

подальше збільшення приведе до того, що змінна тане від’ємною. А це означає, що розв’язок – недопустимий.

Отже, якщо (ця змінна стане базисною), то

=0 (стане небазисною);

;

;

.

Це означає, що перейшли у інший ДБР (вершину В).

[Муртаф, с.30]

Пусть ДБР соответствует преобразованной задаче (8)-(10). Перейдем от него к новому ДБР .

При этом рассмотрим возможность того, что только одна небазисная переменная станет возрастать, принимая положительные значения, в то время, как остальные небазисные переменные останутся нулевыми.

Запишем систему ограничений (9) преобразованной задачи по столбцам

,

где - компонента вектора , которая соответствует переменной .

Обозначим и перепишем систему ограничений:

.

Пусть начиная с нуля возрастает переменная , остальные небазисные переменные остаются нулевыми. Значит вектор базисных переменных изменяется согласно уравнению

. (11)

В нашем примере

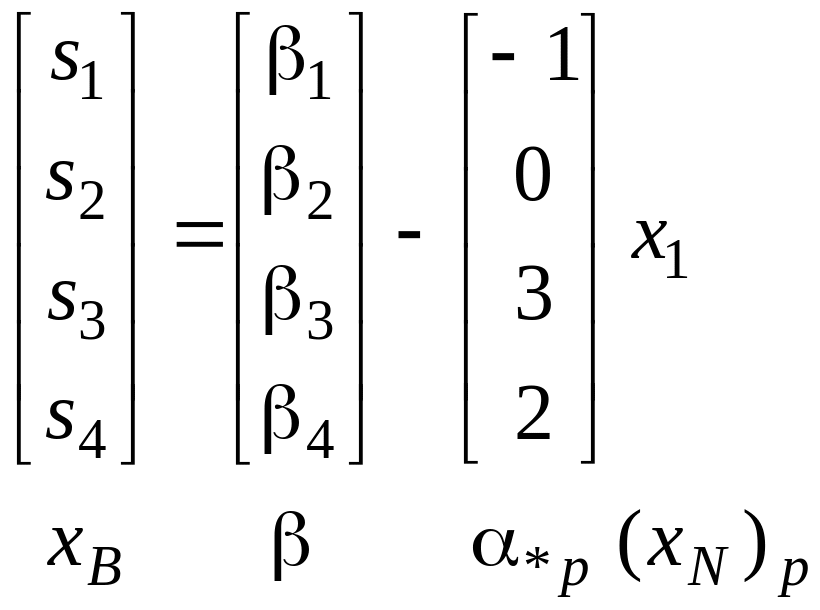
Вектор будем называть ведущим.

При этом, в зависимости от значений компонент ведущего вектора возможны 3 следующих случая:

• Если 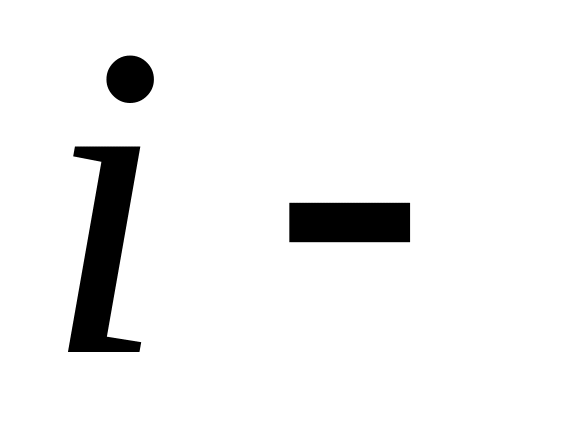я компонента вектора 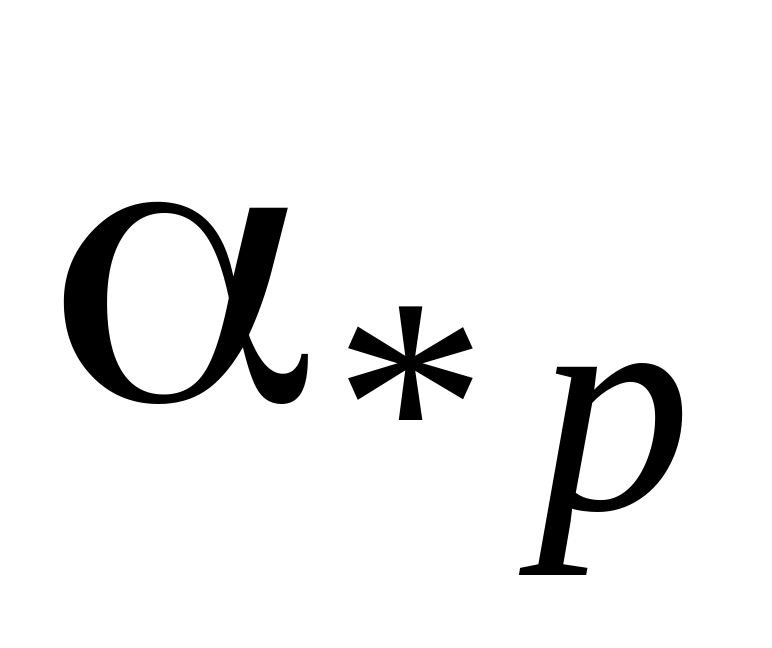равна нулю ( 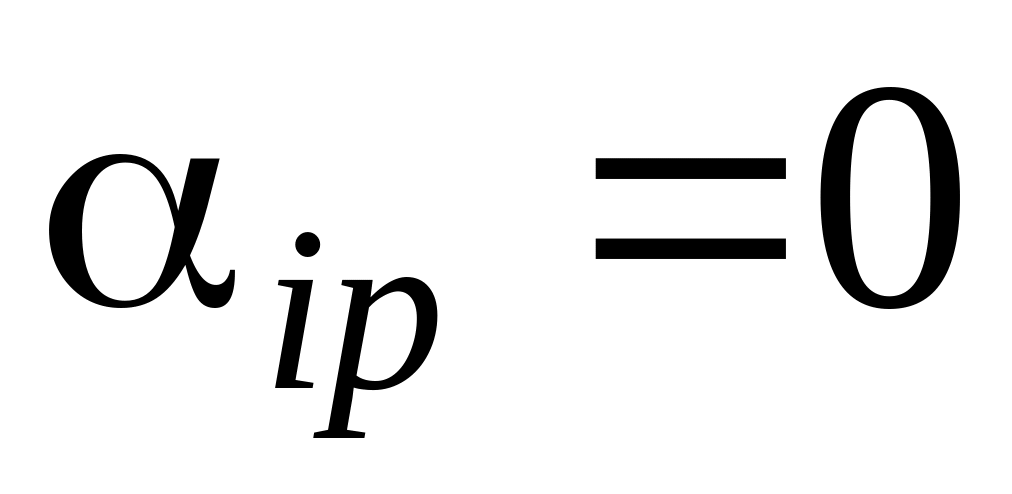) – соответствующий ей элемент вектора (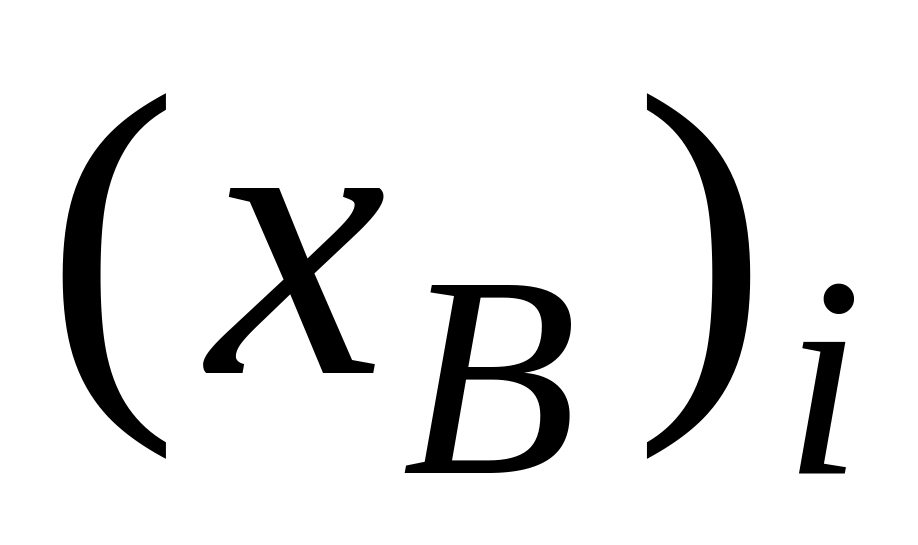 ) останется без изменений;

• если я компонента отрицательна ( 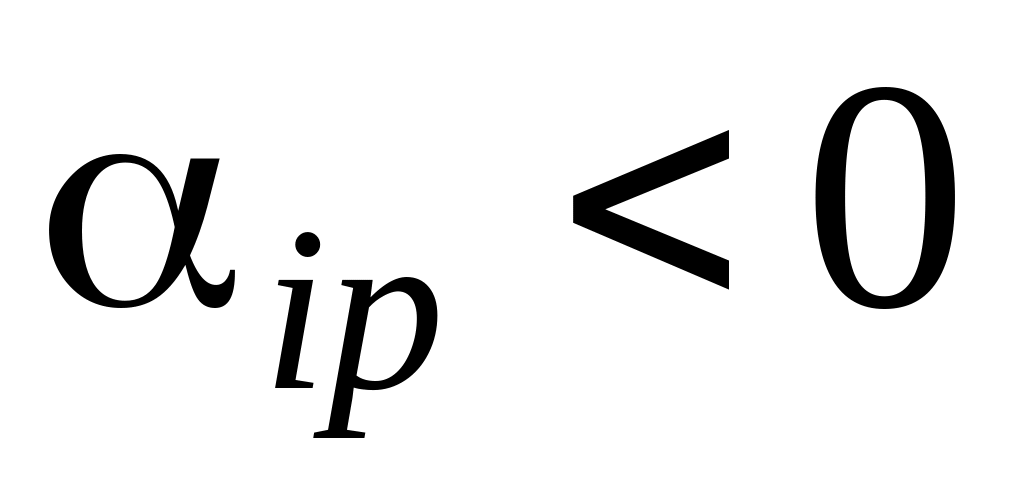) – соответствующий ей элемент вектора будет увеличиваться;

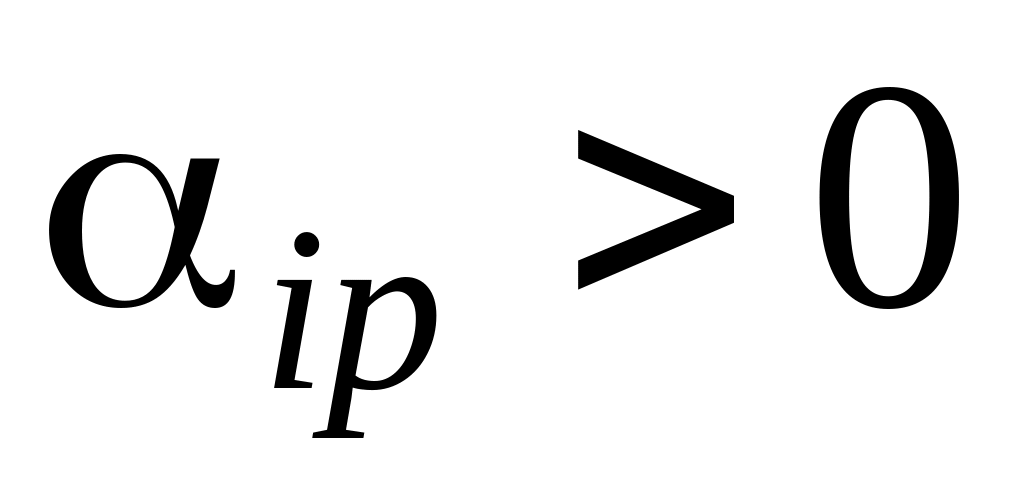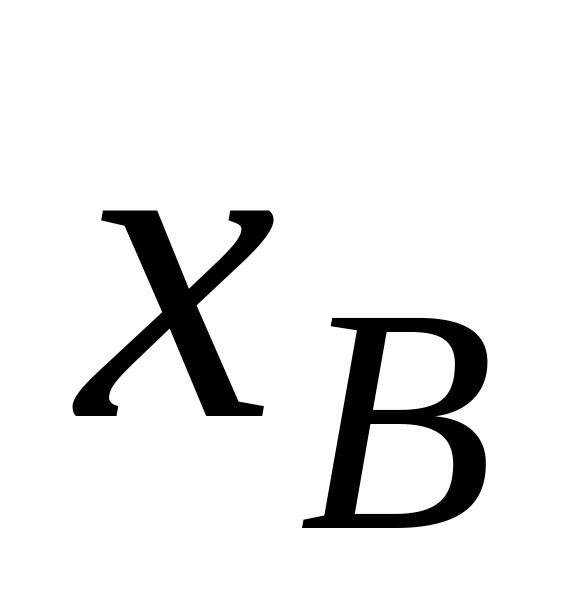• если я компонента положительна ( ) – соответствующий ей элемент вектора будет уменьшаться и станет меньше нуля, когда величина 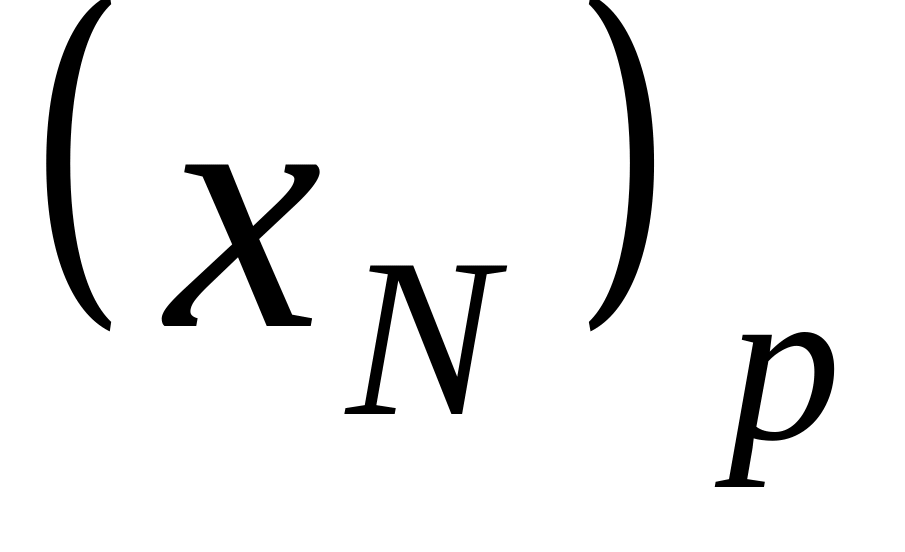сделается достаточно большой. Этого допустить нельзя, т.к. будет нарушена допустимость решения .

Отсюда получаем максимально допустимое увеличение значения

(12)

где и – i – е элементы векторов и соответственно.

Пусть минимум в этом уравнении достигается при тогда, если

,

то в новом ДБР имеем:

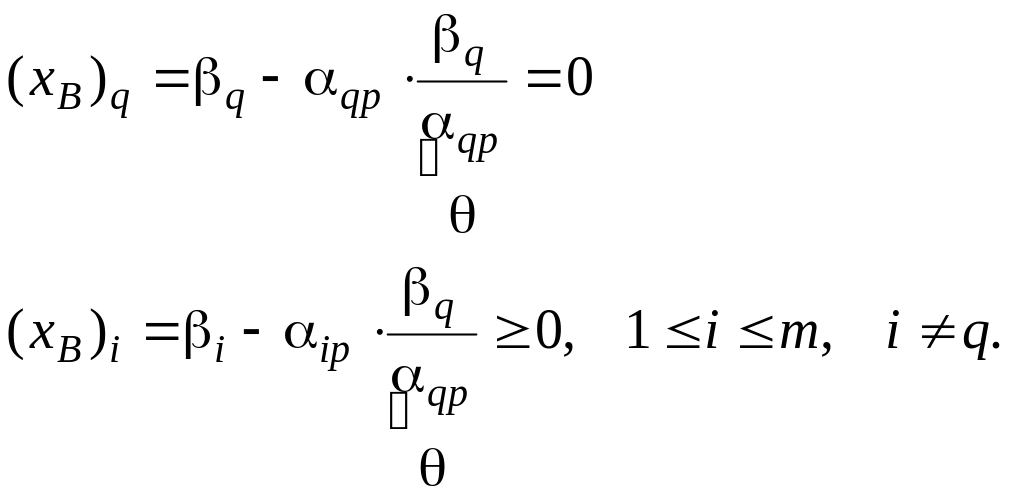
Отметим, что выбор q однозначен. Если уже выбрана увеличиваемая небазисная переменная (р), то базисная (q), которая первая обратится в нуль, определяется величинами и . Если в нуль обращаются одновременно две или более базисных переменных (имеем дело с вырожденным случаем), выбрать мы должны только одну из них.

Итак, мы пришли с следующей ситуации: переменная стала базисной со значением , а переменная – небазисной (со значением 0). Это означает такую перестановку в разбиении матрицы А, что столбец становится на место q-го столбца матрицы В. В этом случае будем говорить, что « входит» в базис, а « выходит» из базиса.

Описанный способ перехода от одного ДБР к другому называется операцией замещения.

Осталось показать, что новая точка , на самом деле является ДБР.

Теорема.

Решение , получаемое в результате операции замещения, является ДБР.

Доказательство.

То, что точка допустима – очевидно (значение выбиралось таким образом, что новая точка удовлетворяет ограничениям ).

Осталось доказать, что решение - базисное решение.

Базисная матрица, соответствующая исходному решению , имеет вид:

Новая базисная матрица такова:

(столбец заменен на столбец ).

Покажем, что векторы матрицы являются линейно независимыми (т.е. что это действительно базисная матрица). Проведем доказательство от противного.

Предположим, что векторы матрицы линейно зависимы, т.е. существуют числа не все равные нулю, что

Очевидно, что , иначе получили бы, что векторы линейно зависимы. Это невозможно в силу того, что любая подсистема системы линейно независимых векторов также является линейно независимой. Значит можно записать:

(13)

!!!!Отметим, что столбец в представлении вектора через (m-1) вектор отсутствует.

С другой стороны по определению вектора имеем:

Помножим слева на В.

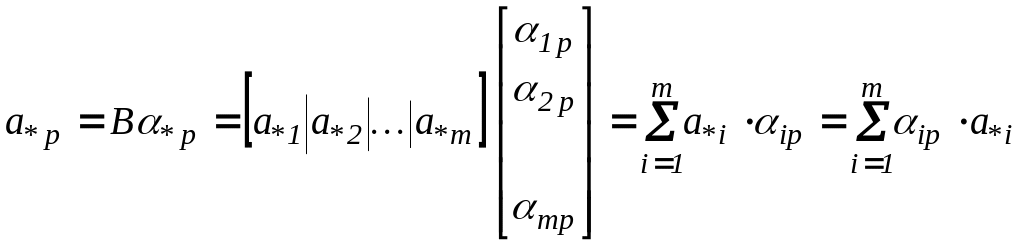(14)

Отметим, что в (14) коэффициент ведущего столбца , так как он определяется соотношением (12). Из (13) и (14) следует, что вектор может быть представлен в виде двух различных линейных комбинаций линейно – независимых векторов . Коэффициенты при q-ом столбце равны соответственно нулю (в (13)) и не нулю (в (14)). Но это противоречит линейной независимости данных векторов. Пришли к противоречию. Значит столбцы матрицы линейно-независимы ( является базисной матрицей), а соответствующее решение – ДБР. . Ч.т.д.

Отметим 2 частных случая, которые могут иметь место для ДБР [Пападимитриу, с. 47].

Частный случай 1. Если вырожденно (некоторое ), а соответствующее положительно, то в силу (12) . В этом случае базис меняется, однако мы не движемся в пространстве , а остаемся в той же вершине.

Рассмотрим ДБР , которому соответствует базис ß = .

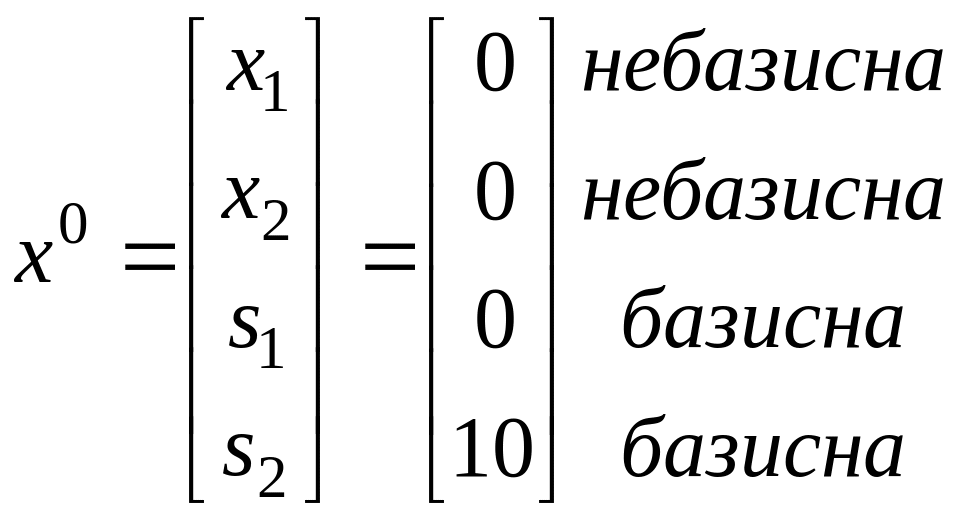
(11)

Начнём увеличивать небазисную переменную (вводим ее в число базисных) ; минимум соответствует ., следовательно, будет выведена из базиса. Пересчитаем значения базисных переменных:

(стала базисной),

(стала небазисной),

(базисная, осталась без изменений)

= 0 (небазисная, залишилась без змін)

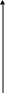
Частный случай 2. Если все элементы ведущего столбца неположительные, мы можем двигаться сколь угодно далеко, оставаясь при этом в допустимом множестве.

Пусть имеем ЗЛП с такой системой ограничений.

Рассмотрим ДБР , которому соответствует базис ß = .

Для этого приведем к диагональному виду относительно переменных .

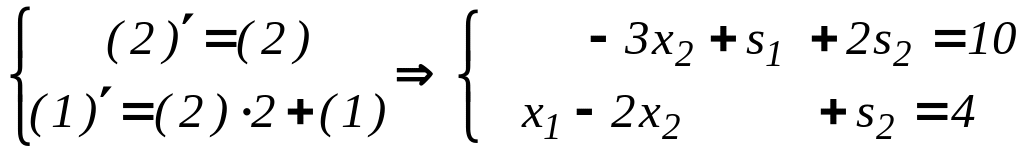
Значит

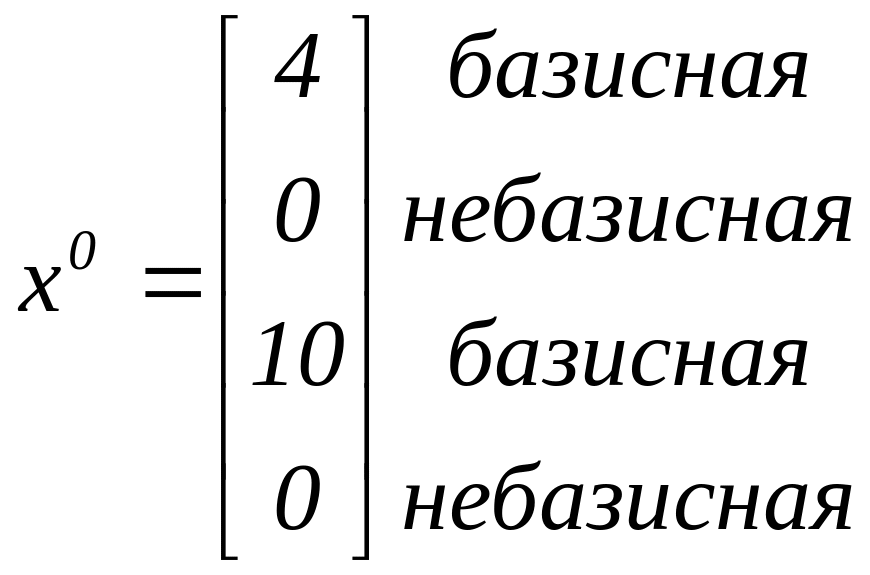
Начнём увеличивать . Так как все элементы ведущего вектора , то какое бы значение не приняла переменная , всегда найдутся такие значения , что равенства системы ограничений всегда будут выполняться, т.е. мы все равно остаемся в допустимой области.

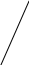
2

4

Вернёмся к рассмотрению операции замещения, в результате которой из ДБР перешли к .