
- •3.6.3 Применение критерия согласия Пирсона
- •3.6.4 Точечная оценка параметров некоторых законов распределения случайных величин
- •3.6.5 Интегральная оценка математического ожидания и среднего квадратичного отклонения при различных распределениях случайной величины
- •3.7 Экспертный метод оценки объектов
3.6.5 Интегральная оценка математического ожидания и среднего квадратичного отклонения при различных распределениях случайной величины
Наиболее важными
числовыми характеристиками являются
математическое ожидание и дисперсия
(или среднее квадратичное отклонение).
Точечные оценки этих величин по формулам
(6) и (61) целиком зависят от объема выборки
и могут значительно отклоняться от
истинных значений
![]() и
и
![]() ,
особенно при малом числе измерений. В
ряде задач требуется не только найти
подходящее значение
и
,
но и оценить их точность и надежность.
Для решения этого вопроса используют
доверительные интервалы и доверительные
вероятности. Пусть, например,
является точечной оценкой математического
ожидания М(Х)=m. Требуется оценить
возможное отклонение
,
особенно при малом числе измерений. В
ряде задач требуется не только найти
подходящее значение
и
,
но и оценить их точность и надежность.
Для решения этого вопроса используют
доверительные интервалы и доверительные
вероятности. Пусть, например,
является точечной оценкой математического
ожидания М(Х)=m. Требуется оценить
возможное отклонение
![]() от m на уровне значимости q, то есть найти
такой доверительный интервал [m–,
m+],
который с надежностью 1–q покроет точку
m. Последнее запишем так:
от m на уровне значимости q, то есть найти
такой доверительный интервал [m–,
m+],
который с надежностью 1–q покроет точку
m. Последнее запишем так:
|
(69) |
Вероятность попадания в заданный интервал находим по формуле
, |
(70) |
где
![]() и
и
![]() – значения интегральной функции
распределения на концах отрезка. Но
тогда нужно знать распределение случайной
величины
,
которое, вообще говоря, отличается от
распределения самой величины Х.
Аналогичная задача ставится и для оценки
.
– значения интегральной функции
распределения на концах отрезка. Но
тогда нужно знать распределение случайной
величины
,
которое, вообще говоря, отличается от
распределения самой величины Х.
Аналогичная задача ставится и для оценки
.
В случае нормального распределения величины Х этот вопрос хорошо изучен и получены следующие интервальные оценки:
|
(71) |
|
(72) |
где и S – вычислены по формулам (6) и (9); q – уровень значимости; tp,f – значение критерия Стьюдента (приложение 3, табл. 1) с числом степеней свободы f=n–1; – значения квантилей распределения Пирсона, найденные для числа степеней свободы f по табл. 4 приложения 3; n – объем выборки.
Если же распределение случайной величины Х не является нормальным или вообще неизвестно, то при достаточно большой выборке (n>30) по теореме Ляпунова можно считать, что случайные величины и S, рассчитанные по формулам (6) и (9), распределены приблизительно нормально. Тогда для получения интервальных оценок можно воспользоваться формулой (70). На основании этих рассуждений получим расчетные формулы
|
(73) |
|
(74) |
где
![]() и
и
![]() – длины доверительных интервалов,
покрывающих истинные значения
и
случайной величины Х с вероятностью р;
– длины доверительных интервалов,
покрывающих истинные значения
и
случайной величины Х с вероятностью р;
![]() – функция, обратная функции Лапласа; S
– эмпирический стандарт выборки объема
n.
– функция, обратная функции Лапласа; S
– эмпирический стандарт выборки объема
n.
Тогда будем иметь
|
(75) |
3.7 Экспертный метод оценки объектов
Экспертный метод решения задач основан на использовании обобщенного опыта и интуиции специалистов экспертов. Число экспертов, входящих в группу, зависит от требуемой точности средних оценок и должно составлять от 7 до 20 человек. При заочном опросе верхний предел количества опрашиваемых экспертов не ограничивается.
Экспертные методы сравнения используют методы основанные на шкалировании.
При сравнении применяют одну из трех шкал:
шкалу уровней (с принятой величиной уровня Q сравниваются все остальные величины Qj:(Q1-Q=
 Q);
Q);
шкалу порядка (результатом оценки качества является ранжированный ряд сравниваемых величин (Q1<Q2<…<Qn);
шкалу отношений (сравнение величины с эталоном по принципу Qi/Qэталон=q).
Экспертный метод предполагает проверку согласованности мнений экспертов, предполагаемых для включения в состав экспертной комиссии. Для этого каждому эксперту предлагается дать оценку определенному свойству объекта (Qi). Если мнение аттестуемого эксперта не оказывается крайним (наибольшим или наименьшим) в полученном ряду оценок, то квалификационный уровень его можно считать соответствующим уровню комиссии.
В противном же
случае данную им оценку считают
«противоречивой» групповому мнению
при доверительной вероятности 0,95 (или
![]() =0,05),
если
=0,05),
если
![]() ,где
,где
![]() -
среднее арифметическое значение оценки;
S – среднее квадратическое отклонение
индивидуальных оценок в группе.
-
среднее арифметическое значение оценки;
S – среднее квадратическое отклонение
индивидуальных оценок в группе.
Значение коэффициента
![]() для
=0,05
принимают из таблицы 3.7.1 в зависимости
от количества членов группы
для
=0,05
принимают из таблицы 3.7.1 в зависимости
от количества членов группы
Таблица 3.7.1
Число экспертов в группе |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Коэффициент |
1,15 |
1,46 |
1,67 |
1,82 |
1,94 |
2,03 |
2,11 |
2,18 |
Более глубокой является оценка согласованности мнений группы по коэффициенту конкордации W, представляющего собой общий коэффициент ранговой корреляции для группы.
Такая оценка производится по количественным оценкам некоторых свойств (факторов),оказывающих влияние на один конечный результат (качество).
Коэффициент конкордации рассчитывается по формуле:
![]() ,
(76)
,
(76)
где m – число экспертов в группе; n – число оцениваемых факторов.
В зависимости от
степени согласованности мнений экспертов
коэффициент конкордации может принимать
значения от нуля (при отсутствии
согласованности) до единицы (при полном
единодушии). Для оценки значимости
коэффициента конкордации необходимо
и достаточно, чтобы
![]() .
Значение
.
Значение
![]() принимают по таблице в зависимости от
числа степеней свободы f=n-1 и принятой
доверительной вероятности.
принимают по таблице в зависимости от
числа степеней свободы f=n-1 и принятой
доверительной вероятности.
1
Пусть некоторая функция у=у(х)
представляет из себя таблицу, где xi
– значение аргумента, yi
– соответствующее значение функции.
Требуется найти значение функции для
аргумента х1<х<х2
по данным значения у1<у<у2
или наоборот по данному у
найти х.
Предположим, что на участке (х1,
х2)
график функции имеет линейную зависимость,
тогда уравнение прямой будет иметь вид
![]() .
Поскольку
отрезок [х1,
х2]
мал, то в точке х
ордината у(х)
мало отличается от ординаты прямой. Из
уравнения прямой находим неизвестное
х
или у.
Такой метод называется линейное
интерполирование.
.
Поскольку
отрезок [х1,
х2]
мал, то в точке х
ордината у(х)
мало отличается от ординаты прямой. Из
уравнения прямой находим неизвестное
х
или у.
Такой метод называется линейное
интерполирование.

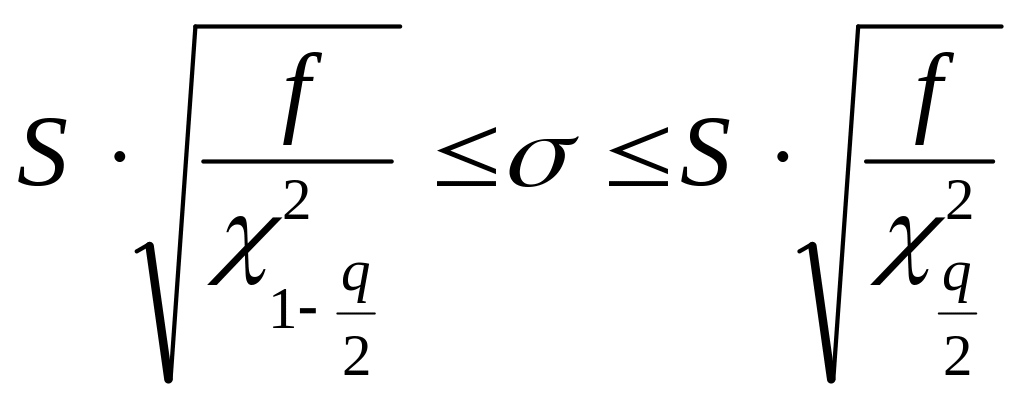 ,
,