3.2.2. Рівняння прямої на площині.

Найпростішою з ліній є пряма. Різним способам завданням прямої відповідають в прямокутній системі координат різні види її рівнянь.

Рівняння прямої з кутовим коефіцієнтом

Нехай на площині Оху задана довільна пряма, не паралельна осі Оу. Її положення цілком визначається ординатою b точки N(0; b) перетину з віссю Оу і кутом а між віссю Ох і прямій (див. рис. 19).

Під кутом нахилу прямої розуміється найменший кут, на який потрібно повернути навколо точки перетину прямої і осі Ох проти годинникової стрілки вісь Ох до її збігу з прямій.

рис. 19.

Візьмемо на прямій довільну точку М(х;у) (див. рис. 19). Проведемо через точку N вісь , паралельну осі Ох і однаково з нею направлену. Кут між віссю і прямою рівний . У системі 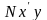точка М має координати х і у - b. З визначення тангенса кута виходить рівність , тобто . . Введено позначення , отримуємо рівняння

(2.2)

яке задовольняє координати будь-якої точки М(х;у) прямої. Можна переконатися, що координати будь-якої точки Р(х;у), лежить поза даною прямою, рівнянню (2.2) не задовольняють.

Число , називається кутовим коефіцієнтом прямої, а рівняння (2.2) - рівнянням прямої з кутовим коефіцієнтом.

Якщо пряма проходить через початок координат, то і, отже, рівняння цієї прямої матиме вигляд .

Якщо пряма паралельна осі Ох, то , отже, і рівняння (2.2) прийме вигляд

.

Якщо пряма паралельна осі Оу, то, рівняння (2.2) втрачає сенс, оскільки для неї кутовий коефіцієнт не існує.

В цьому випадку рівняння прямої матиме вигляд

(2.3)

де а - абсциса точки перетину прямої з віссю Ох. Відзначимо, що рівняння (2.2) і (2.3) є рівняння першого ступеня.

Загальне рівняння прямої

Розглянемо рівняння першого ступеня відносно х і у в загальному вигляді

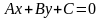(2.4)

де A, В, С - довільні числа, причому А і В не рівні нулю одночасно.

Покажемо, що рівняння (2.4) є рівняння прямої лінії. Можливі два випадки.

Якщо , то рівняння (2.4) має вигляд , причому , тобто . Це є рівняння прямої, паралельної осі Оу і що проходить через точку .

Якщо , то з рівняння (2.4) отримуємо . Це є рівняння прямої з кутовим коефіцієнтом .

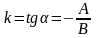Отже, рівняння (2.4) є рівняння прямої лінії, воно називається загальним рівнянням прямої.

Деякі окремі випадки загального рівняння прямої:

1) якщо , то рівняння приводиться до вигляду . Це є рівняння прямої, паралельною осі Ох;

2) якщо , то пряма паралельна осі Oy;

3) якщо , то отримуємо . Рівнянню задовольняють координати точки O(0;0), пряма проходить через початок координат.

Рівняння прямої, що проходить через дану точку в даному напрямі

Нехай пряма проходить через точки і її напрям характеризується кутовим коефіцієнтом k. Рівняння цієї прямої можна записати у вигляді у=kx+b, де b — поки невідома величина. Оскільки пряма проходить через точку , то координати точки задовольняють рівнянню прямої: . Звідси . Підставляючи значення b в рівняння , отримаємо шукане рівняння прямої , тобто

(2.5)

Рівняння (2.5) з різними значеннями k називають також рівняннями пучка прямих з центром в точці . З цього пучка не можна визначити лише пряму, паралельну осі Оу.

Рівняння прямої, що проходить через дві точки

Нехай пряма проходить через точки і . Рівняння прямої, що проходить через точку має вигляд

(2.6)

де k — поки невідомий коефіцієнт.

Оскільки пряма проходить через точку , то координати цієї точки повинні задовольняти рівнянню (2.6): .Звідси знаходимо . Підставляючи знайдене значення k в рівняння (2.6), отримаємо рівняння прямої, що проходить через точки М₁ і М₂:

(2.7)

Передбачається, що в цьому рівнянні .

Якщо x₂=x₁, то пряма, що проходить через точки і , паралельна осі ординат. Її рівняння має вид х = х₁.

Якщо у₂ = у₁, то рівняння прямої може бути записане у вигляді у = у₁, пряма М₁М₂ паралельна осі абсцис.

Рівняння прямої у відрізках

Н ехай пряма перетинає вісь Ох в точці М₁(а; 0), а вісь Оу — в точці М₂(0; b) (див. рис. 20). В цьому випадку рівняння (2.7) прийме вигляд

тобто .

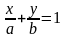
Ц

рис. 20.

е рівняння називається рівнянням прямої у відрізках, оскільки числа а і b показують, які відрізки відсікає пряма на осях координат.

Рівняння прямої, що проходить через дану точку перпендикулярно даному вектору

Знайдемо рівняння прямої, що проходить через задану точку М₀(x₀; y₀) перпендикулярно даному ненульовому вектору .

В ізьмемо на прямій довільну точку M(x; у) і розглянемо вектор =(x–x₀;у–y₀), (див. рис. 21). Оскільки вектори і перпендикулярні, то їх скалярний добуток рівний нулю: , тобто

(2.8)

рис. 21.

Рівняння (2.8) називається рівнянням прямої, що проходить через задану точку перпендикулярно заданому вектору.

Вектор , перпендикулярний прямій, називається нормальним вектором цієї прямої. Рівняння (2.8) можна переписати у вигляді

(2.9)

де А і В — координати нормального вектора, - вільний член. Рівняння (2.9) є загальне рівняння прямої (див. (2.4)).

Полярне рівняння прямої

З найдемо рівняння прямої в полярних координатах. Її положення можна визначити, вказавши відстань р від полюса О до даної прямої і кут а між полярною віссю ОР і віссю l, що проходить через полюс О перпендикулярно дану пряму (див. рис. 22).

Д

рис. 22.

ля будь-якої точки 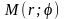на даній прямій маємо:

.

З іншого боку,

Отже

. (2.10)

Отримане рівняння (2.10) і є рівняння прямої в полярних координатах.

Нормальне рівняння прямої

Нехай пряма визначається заданням р і а (див. рис. 23). Розглянемо прямокутну систему координат Оху. Введемо полярну систему, взявши О за полюс і Ох за полярну вісь. Рівняння прямої можна записати у вигляді

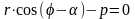тобто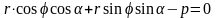

рис. 23.

Але, через формули, що зв'язують прямокутні і полярні координати, маємо: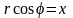 , . Отже, рівняння (2.10) прямої в прямокутній системі координат прийме вигляд

. (2.11)

Рівняння (2.11) називається нормальним рівнянням прямої.

Покажемо, як привести рівняння (2.4) прямої до вигляду (2.11).

Помножимо всі члени рівняння (2.4) на деякий множник . Отримаємо . Це рівняння повинне звернутися в рівняння (2.11). Отже, повинна виконуватися рівність: , , . З першої двох рівності знаходимо, тобто Множник називається нормуючим множником. Згідно третьої рівності знак нормуючого множника протилежний знаку вільного члена із загального рівняння прямої.

Приклад 2.2. Привести рівняння –3x + 4у + 15 = 0 до нормального вигляду.

○ Знаходимо нормуючий множник 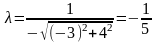. Помноживши дане рівняння на, отримаємо шукане нормальне рівняння прямої: .●
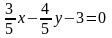