Глава 4.4. Виды и формы средних величин.

Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности в конкретных условиях места и времени. Величина средней дает характеристику всей совокупности и характеризует ее в отношении одного, данного признака.

Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности.

Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников.

Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения, вызванные основным фактором.

Статистическая обработка методом средних величин заключается в замене индивидуальных значений варьирующего признака некоторой уравновешенной средней величиной Х .

Например, индивидуальная выработка у 5 операционистов коммерческого банка за день составила 136, 140, 154 и 162 операции. Чтобы получить среднее число операций за день, выполненных одним операционистом, необходимо сложить эти индивидуальные показатели и полученную сумму разделить на количество операционистов:

Как видно из приведенного примера, среднее число операций не совпадает ни с одним из индивидуальных, так как ни один операционист не сделал 150 операций. Но если мы представим себе, что каждый операционист сделал по 150 операций, то их общая сумма не изменится, а будет также равна 750. Таким образом, мы пришли к основному свойству средних величин: сумма индивидуальных значений признака равна сумме средних величин.

Это свойство еще раз подчеркивает, что средняя величина является обобщающей характеристикой всей статистической совокупности.

Виды средних величин

Средние величины делятся на два больших класса:

Степенные средние:

• Арифметическая

• Гармоническая

• Геометрическая

• Квадратическая

Структурные средние:

• Мода

• Медиана

Самым распространенным видом средней является средняя арифметическая:

• Средняя арифметическая простая

• Средняя арифметическая взвешенная

• Средняя арифметическая для интервального ряда.

Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем данного признака в совокупности данных поровну распределяется между всеми единицами, входящими в данную.

Так, среднегодовая выработка продукции на одного работающего — это такая величина объема продукции, которая приходилась бы на каждого работника, если бы весь объем выпущенной продукции в одинаковой степени распределялся между всеми сотрудниками организации. Среднеарифметическая простая величина исчисляется по формуле:

Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности

Пример 1. Бригада из 6 рабочих получает в месяц 3 3,2 3,3 3,5 3,8 3,1 тыс.руб. Найти среднюю заработную плату

Решение:

(3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 (тыс. руб.)

Средняя арифметическая взвешенная Если объем совокупности данных большой и представляет собой ряд распределения, то исчисляется взвешенная среднеарифметическая величина. Так определяют средневзвешенную цену за единицу продукции: общую стоимость продукции (сумму произведений ее количества на цену единицы продукции) делят на суммарное количество продукции.

Представим это в виде следующей формулы:

— цена за единицу продукции; — количество (объем) продукции.

Средняя арифметическая взвешенная равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков).Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Пример 2. Найти среднюю заработную плату рабочих цеха за месяц

Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:

Ответ: 3,35 тыс.руб.

Средняя арифметическая для интервального ряда При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.

Средние, вычисляемые из интервальных рядов являются приближенными.

Пример 3. Определить средний возраст студентов вечернего отделения.

Средние, вычисляемые из интервальных рядов являются приближенными. Степень их приближения зависит от того, в какой мере фактическое распределение единиц совокупности внутри интервала приближается к равномерному.

При расчете средних в качестве весов могут использоваться не только абсолютные, но и относительные величины (частость):

Средняя гармоническая Используется в тех случаях когда известны индивидуальные значения признака Х и произведение Х*f , а частоты f неизвестны.

В примере ниже Х — урожайность известна, f — площадь неизвестна (хотя её можно вычислить делением валового сбора зерновых на урожайность), Х*f — валовый сбор зерна известен.

Среднегармоническую величину можно определить по следующей формуле:

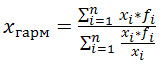
Пример4. Вычислить среднюю урожайность по трем фермерским хозяйствам

В тех случаях, когда произведение Х*f одинаково или равно 1 (z = 1) для расчета применяют среднюю гармоническую простую, вычисляемую по формуле:

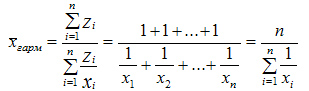
Средняя гармоническая простая — показатель, обратный средней арифметической простой, исчисляемый из обратных значений признака.

Средняя геометрическая простая дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Ее можно определить по следующей формуле:

Средние геометрические величины наиболее часто используются при анализе темпов роста экономических показателей, исчисляемых из обратных значений признака.

Для расчетов средней геометрической простой используется формула:

где:

— цепной коэффициент роста

n — число этих коэффициентов роста

П— знак произведения

m — количество уровней ряда

— значение начального уровня ряда

— значение конечного уровня ряда .

Средняя квадратическая Средние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической.

Среднеквадратические величины используются для расчета некоторых показателей, например коэффициента вариации, характеризующего ритмичность выпуска продукции. Он определяет среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:

Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.

Средняя квадратическая простая вычисляется по формуле:

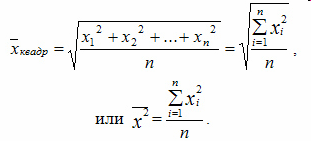
Средняя квадратическая взвешенная:

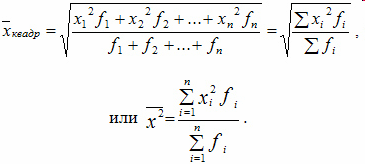
В статистике могут применяться также степенные средние 3-го и более высоких порядков.

Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены ,в основном, модой и медианой.

Мода — это наиболее часто встречающийся вариант ряда.

Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей.

Модой для дискретного ряда является варианта, обладающая наибольшей частотой.

При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

где:

— значение моды

— нижняя граница модального интервала

h — величина интервала

— частота модального интервала

— частота интервала, предшествующего модальному

— частота интервала, следующего за модальным.

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии

частот сначала вычисляют полусумму частот  ,

а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

Ме = (n(число признаков в совокупности) + 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков, находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

где:

— искомая медиана

   — нижняя граница интервала, который содержит медиану

  — величина интервала

— сумма частот или число членов ряда

— сумма накопленных частот интервалов, предшествующих медианному

 — частота медианного интервала.

Пример 5. Найти моду и медиану.

Решение:

В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).

Рассчитаем величину моды:

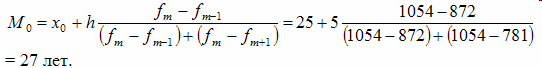
Это значит что модальный возраст студентов равен 27 годам.

Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Уfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:

Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.

Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100 частей.