18. Проверка значимости уравнения регрессии с помощью f критерия Фишера .Расчетный и табличный критерий Фишера.

Проверка значимости коэффициента детерминации осуществляется с помощью -критерия Фишера, расчетное значение которого находится по формуле:

,

,

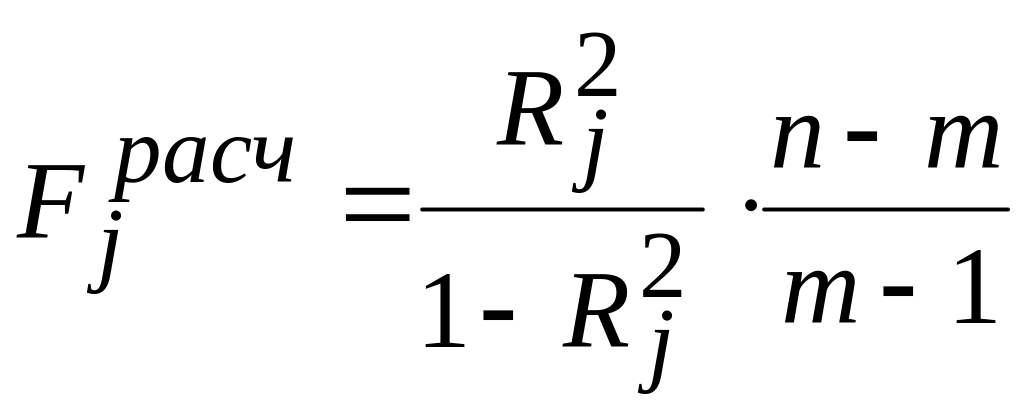где коэффициент множественной корреляции, – количество наблюдений, - количество переменных, – диагональный элемент матрицы .

Фактические значения критерия сравниваются с табличным при и степенях свободы и уровне значимости . Если , то соответствующая -ая объясняющая переменная мультиколлинеарна с другими.

По таблице определяется при уровне значимости и степенями свободы и . Если , то значим (значимо отличается от нуля).

Если необходимо определить связь между двумя случайными величинами при исключении влияния остальных, то используется выборочный частный коэффициент корреляции, который вычисляется по формуле:

,

где – алгебраические дополнения элементов матрицы ,

, , – элементы матрицы .

19.

20. Оценка статистической значимости параметров модели с помощью критерия Стьюдента.

Для проверки значимости параметров модели рассчитывают -статистику Стьюдента для каждого из них по следующей формуле:

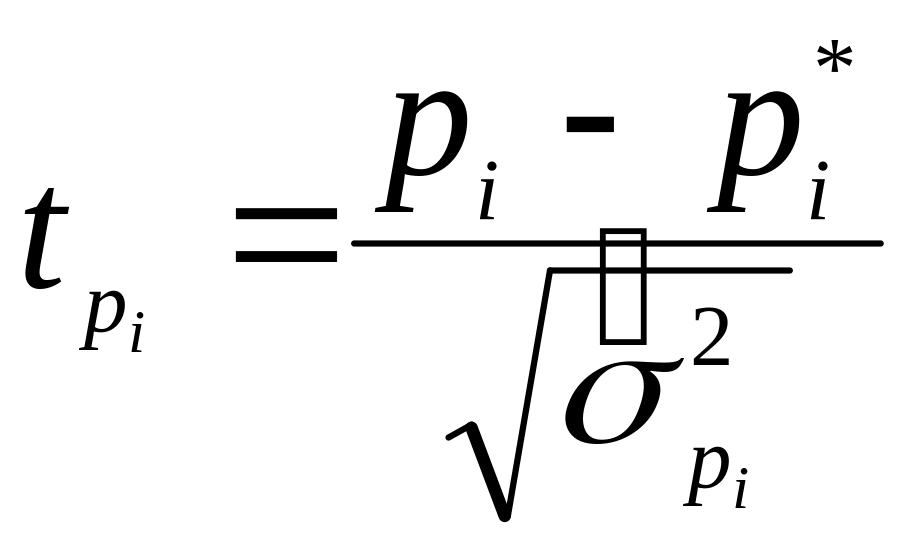
с степенями свободы, где

 оценка рассматриваемого -го параметра;

 гипотетическое значение, которое должен принять параметр ;

 оценка дисперсии параметра (по регрессии);

 размер выборки;

 число оцениваемых параметров модели (для парной регрессии ).

Для оценки параметра выдвигается гипотеза . -статистика Стьюдента принимает вид:

.

Сравниваем рассчитанное значение с табличным для числа степеней свободы и уровня значимости .

Если , то гипотеза отвергается, если , то принимается.

Расчетная формула для оценки значимости параметра аналогична:

.

Оценим значимость параметров модели и . Для этого сначала рассчитаем оценку дисперсии ошибок :

.

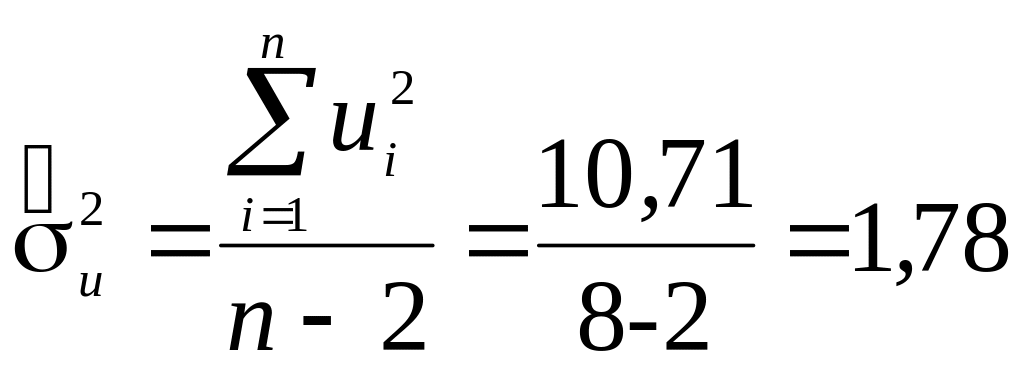Найдем оценку дисперсии и среднеквадратическое отклонение :

,

.

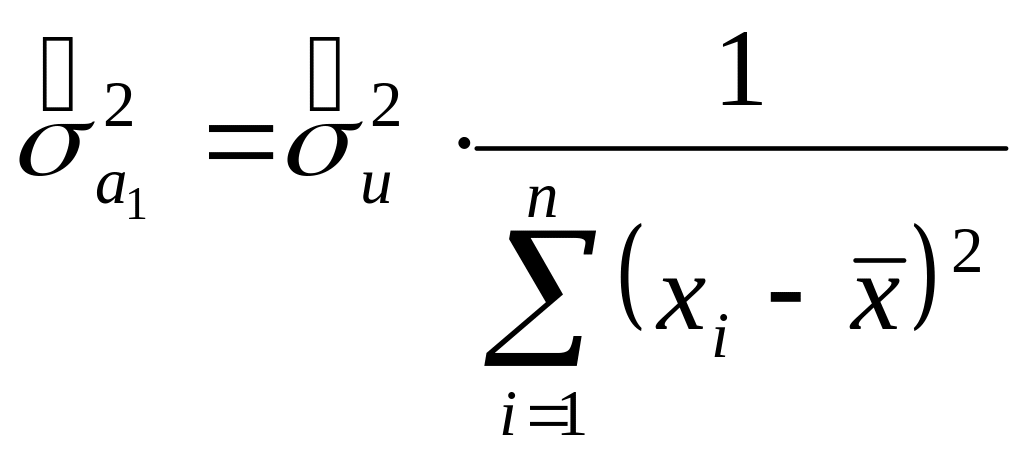Рассчитаем -статистику Стьюдента:

.

Как и в случае с коэффициентом корреляции, найдем для и табличное значение критерия Стьюдента и сравним рассчитанное значение -статистики с табличным:

.

Таким образом, значение коэффициента является значимым.

Найдем оценку дисперсии и среднеквадратическое отклонение :

,

.

Рассчитаем -статистику Стьюдента:

.

Сравним рассчитанное значение -статистики по модулю с табличным для и :

.

Таким образом, для выбранного уровня доверия значение коэффициента не является значимым.

21. Стандартные ошибки коэффициентов Sa0 Sa1 и их расчет

Оценка статистической значимости коэффициентов регрессии и корреля-

ции осуществляется с помощью t -критерия Стьюдента. Расчетные значения

статистик имеют вид:

Для расчета доверительного интервала определяем предельную ошибку для каждого параметра:

,

Формулы для расчета доверительных интервалов имеют следующий вид:

.