5. Коэффициент парной корреляции. Пределы ее изменения.

В экономическом анализе очень важно знать, насколько тесно связаны между собой изучаемые показатели. Для оценки тесноты и направления связи между двумя показателями используется коэффициент парной корреляции. Он рассчитывается по формуле

.

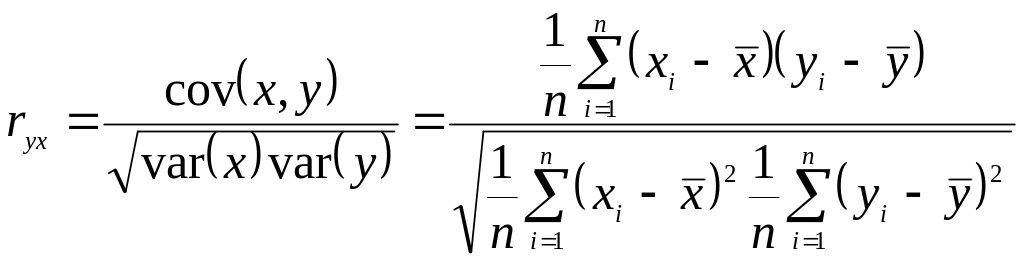Коэффициент корреляции, в отличие от коэффициента регрессии, является показателем относительной меры связи между двумя факторами. Значения коэффициента корреляции всегда находятся в пределах между –1 и +1

.

Положительное значение коэффициента свидетельствует о прямой связи, а отрицательное – об обратной. При приближении коэффициента парной корреляции по абсолютной величине к 1 считается, что связь между показателями тесная, при приближении к 0 – связь отсутствует.

Очень тесной считается связь, когда , средней – когда и слабой, когда .

Коэффициент корреляции характеризует тесноту и направление связи между переменными.

Знак коэффициента корреляции всегда совпадает со знаком коэффициента регрессии.

Связь между коэффициентом корреляции и коэффициентом регрессии выражается следующим соотношением:

,

, .

Рассчитаем коэффициент корреляции. Для этого найдем дисперсии переменных, их среднеквадратические отклонения и ковариацию

, , ,

, , ,

, .

С учетом этого имеем

.

Величина коэффициента парной корреляции, равная 0,981, говорит о прямой и тесной связи между показателями товарооборота и торговой площади

В простой эконометрической модели коэффициент корреляции служит одним из показателей ее качества.

Шкала Чеддока, используемая для качественной оценки коэффициентов корреляции.

Для качественной оценки коэффициента корреляции применяют шкалу Чеддока:

0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-1,0
слабая	заметная	умеренная	высокая	Весьма высокая

6. Оценка значимости линейного коэффициента корреляции с помощью t-критерия Стьюдента.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции : . Фактическое значение t-критерия Стьюдента определяется как и сравнивается с табличным значением. Существует связь между t-критерием Стьюдента и F-критерием Фишера: .

7 . Матрица коэффициентов парной корреляции, её структура, экономическая сущность.

Корреляция — это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Коэффициент корреляции или парный коэффициент корреляции в теории вероятностей и статистике — это показатель характера взаимного стохастического влияния изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R в математической статистике (r в статистике) и может принимать значения от −1 до +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0 — связь слабая или вообще отсутствует. При коэффициенте корреляции равном по модулю единице говорят о функциональной связи, то есть изменения двух величин можно описать математической функцией.

Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.

где   - среднее квадратическое отклонение факторного признака;

       - среднее квадратическое отклонение результативного признака.