
- •Объект автоматического управления.
- •Принципы автоматического управления.
- •Функциональная схема системы управления.
- •Классификация систем автоматического управления.
- •Математическое описание сау
- •Разбиение систем на звенья.
- •Статические и динамические характеристики звеньев систем.
- •Типовые звенья линейных систем.
- •Критерии устойчивости.
Типовые звенья линейных систем.
Любые сложные системы могут быть представлены как совокупность более простых элементов. Для исследования процессов в реальных системах пользуются идеализированными схемами, которые точно описываются математически и приближенно характеризуют реальные звенья систем в заданном диапазоне частот.
В теории управления вводятся некие типовые звенья, которые характеризуются, в независимости от их конструктивного исполнения, назначения, принципа действия и т.п., только своими передаточными функциями.
Классифицируют эти звенья по виду дифференциальных уравнений, описывающих их работу.
Типы звеньев:
Описывающиеся линейными алгебраическими уравнениями относительно выходного сигнала:
а) пропорциональные (безынерционные);
б) запаздывающие;
в) дифференцирующие.
Описывающиеся дифференциальными уравнениями первого порядка с постоянными коэффициентами:
а) инерционно дифференцирующие;
б) инерционные (апериодические, релаксационные);
в) интегрирующие (астатические, нейтральные);
г) интегро – дифференцирующее (упругие).
Описывающиеся дифференциальными уравнениями второго порядка с постоянными коэффициентами:
а) колебательные;
б) апериодические.
Перечень формул, которые будут использованы для описания характеристик типовых звеньев:
Передаточная функция: ,
Переходная функция:
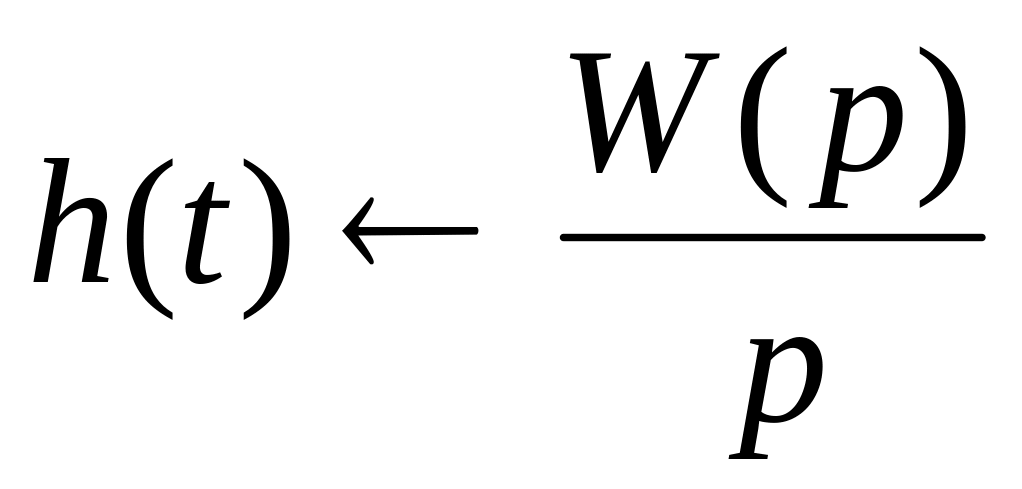 ,
,Весовая функция: ,
Частотная характеристика:
 ,
,АЧХ:
 ,
,ФЧХ:
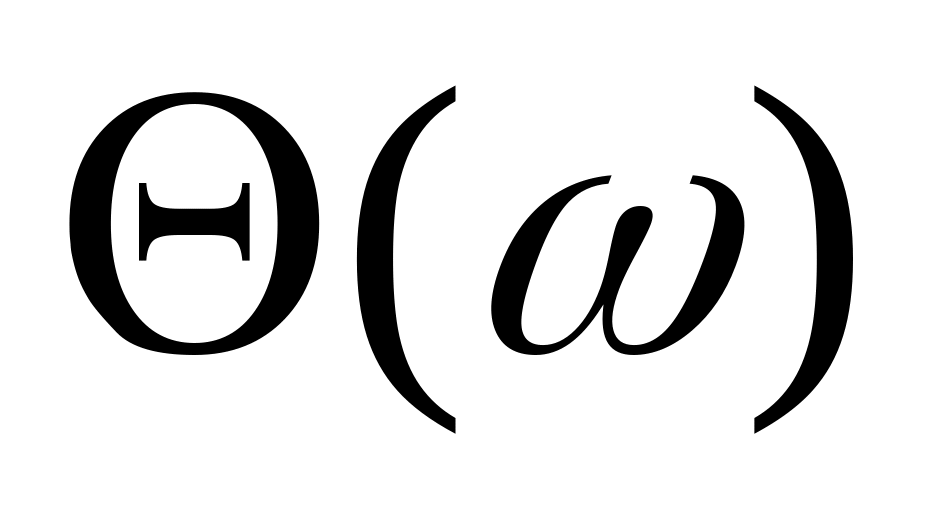 ,
,ЛАЧХ:
 ,
,ЛФЧХ:
 .
.
Пропорциональное звено.
Выходной сигнал прямо пропорционален входному. Описывается уравнением:
y(t) = kx(t), где
k – коэффициент усиления.
Примеры: резистивный делитель напряжения, рычажная передача и др.
Переходя к изображениям, имеем:
Передаточную функцию:
![]()
Переходная функция:
![]() ,
,![]()
Весовая функция:
![]()
Частотная характеристика:
![]()
АЧХ:
![]()

ФЧХ:
 ,
,
ЛАЧХ:
 ,
,
ЛФЧХ:
 .
.
Принятое описание связи между входной и выходной величинами справедливо только для идеального звена и соответствует реальным звеньям лишь при низких частотах ω, меньших ωверх. При ω > ωверх в реальных звеньях коэффициент усиления kус начинает зависеть от частоты и с её увеличением в ∞ падает до 0.
Запаздывающее звено.
Описывается уравнением:
y(t) = x(t-τ), где
τ – время запаздывания.
Примеры: длинные электрические линии без потерь, тепловые объекты, трубопровод, зубчатые передачи и др.
Переходя к изображениям, имеем:
Передаточная функция:
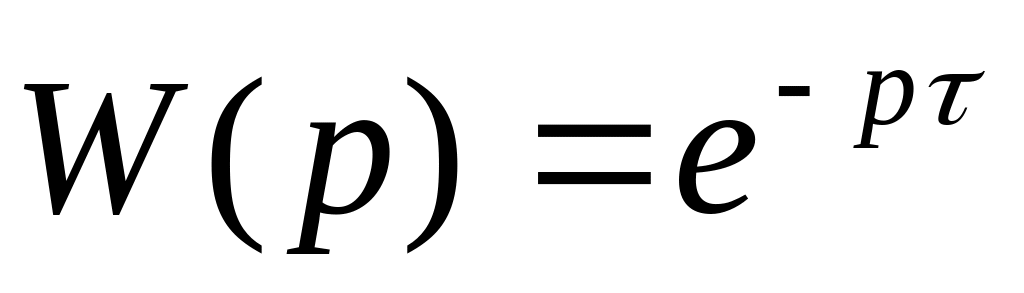
Переходная функция:
 ,
,
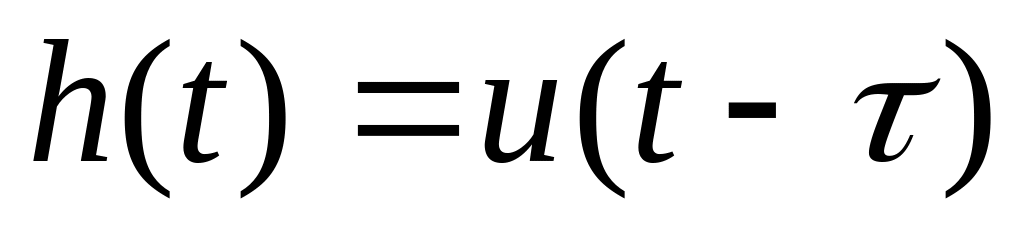
Весовая функция:

Частотная характеристика:
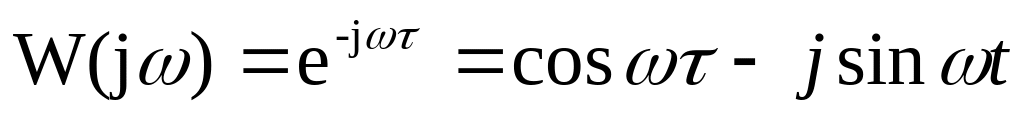
АЧХ:

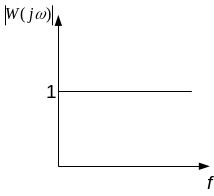
ФЧХ:


ЛАЧХ:
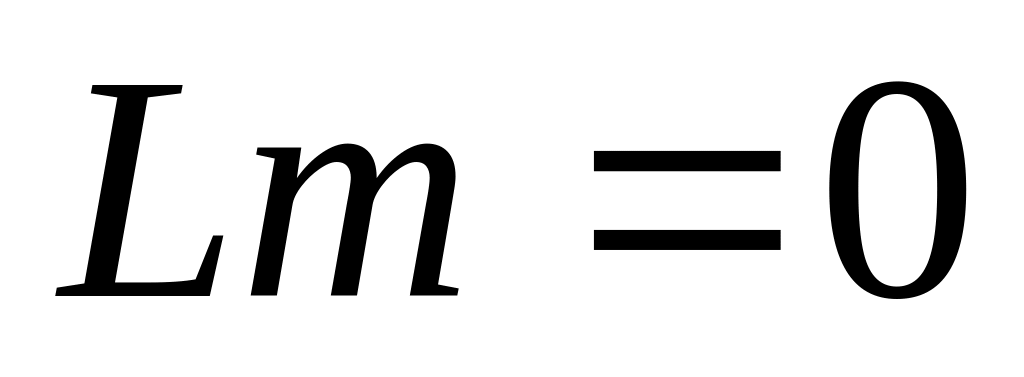
Дифференцирующее звено.
Описывается уравнением:
![]() ,
где
,
где
k – коэффициент усиления.
Примеры: конденсатор
![]() и индуктивность
и индуктивность
![]() .
.
Переходя к изображениям при нулевых начальных условиях, имеем:
Передаточная функция:
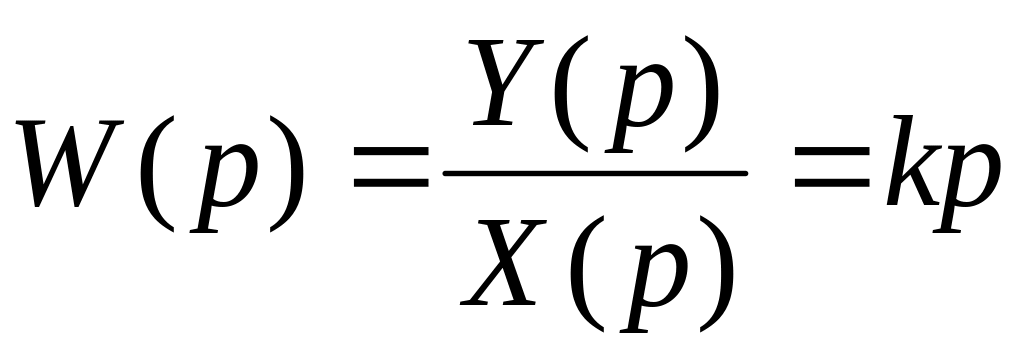 ,
,Переходная функция:
 ,
,
 ,
,
Весовая функция:
 ,
,Частотная характеристика:
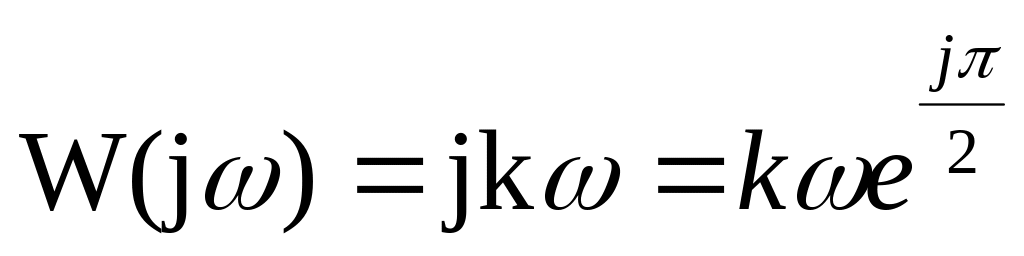 ,
,АЧХ:
 ,
,ФЧХ:
 ,
,ЛАЧХ:
 .
.
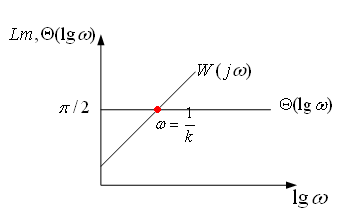
Инерционно-дифференциальное звено.
Описывается дифференциальным уравнением первого порядка:
![]() ,
где
,
где
Т – постоянная времени,
k – коэффициент усиления.
При Т→ 0 уравнение переходит к уравнению, описывающему идеальное дифференциальное звено.
Примеры: конденсатор или индуктивность с учетом активного сопротивления цепи.
Переходя к изображениям при нулевых начальных условиях, получим:
Передаточная функция:
 ,
,
Переходная функция:
 ;
;
 ,
,
Весовая функция:
 ,
,
Частотная характеристика:
 ,
,
АЧХ:
 ,
,
ФЧХ:
 ,
,
ЛАЧХ:
 .
.

![]() вычисляется при частоте
вычисляется при частоте
![]()

Инерционное звено.
Одно из самых распространенных звеньев. Описывается уравнением:
![]() ,
где
,
где
Т – постоянная времени,
k – коэффициент усиления.
Примеры: электродвигатель, термопара.
Переходя к изображениям при нулевых начальных условиях, имеем:
Передаточная функция:
 ,
,
Переходная функция:
 ,
,
 ,
,
Весовая функция:
 ,
,
Частотная характеристика:
 ,
,
АЧХ:
 ,
,
ФЧХ:
 ,
,
ЛАЧХ:
 .
.


Интегрирующее звено.
Описывается уравнением:
![]() или
или
![]() ,
где
,
где
k – коэффициент пропорциональности.
Примеры: вращающийся вал, если входной величиной считать скорость вращения, а выходной – угол поворота вала.
Переходя к изображениям при нулевых начальных условиях, имеем:
Передаточная функция:
 ,
,
Переходная функция:
 ,
,
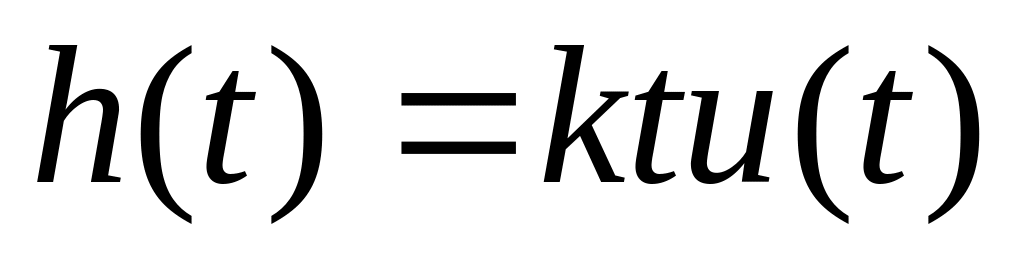 ,
,
Весовая функция:
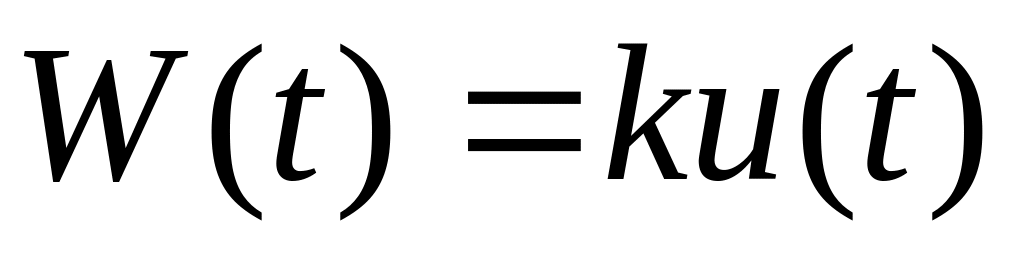 ,
,
Частотная характеристика:
 ,
,
АЧХ:
 ,
,
ФЧХ:
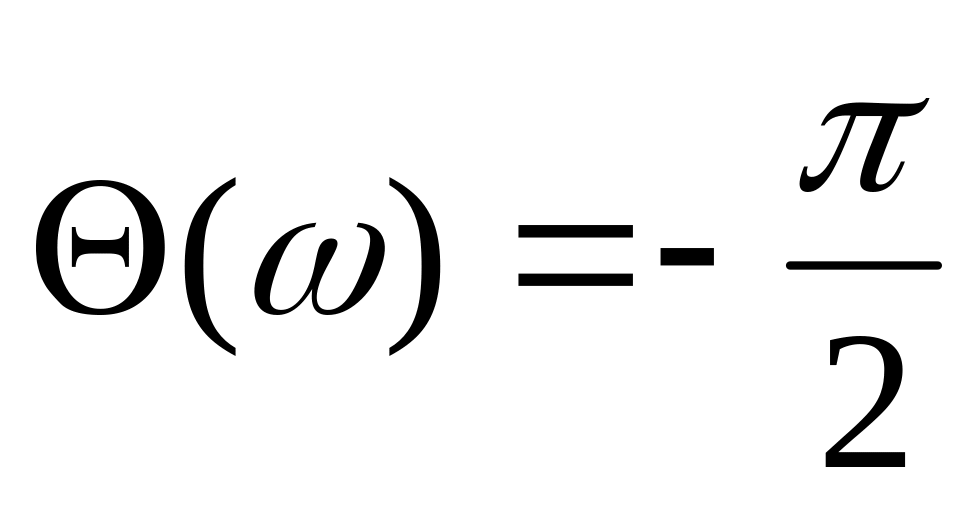 ,
,
ЛАЧХ:
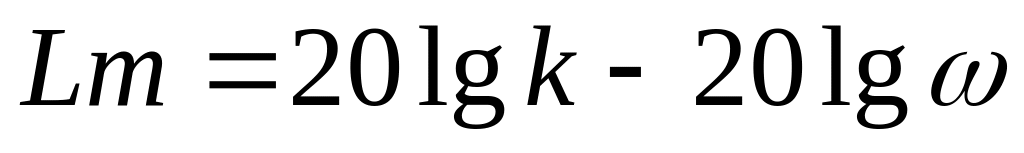 .
.
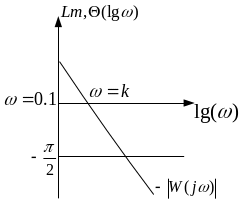
Интегро-дифференцирующее звено.
Описывается дифференциальным уравнением первого порядка:
![]() ,
где
,
где
Т1, Т2 – постоянные времени,
k – коэффициент усиления.
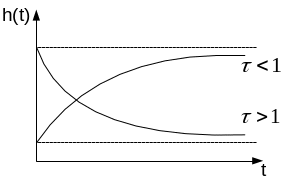
В зависимости от
![]() звено будет обладать различными
свойствами. Если τ < 1, то звено по
свойствам будет приближаться к
интегрирующему и инерционному звеньям,
если τ > 1, то звено ближе к дифференцирующему
и инерционно-дифференциальному звеньям.
звено будет обладать различными
свойствами. Если τ < 1, то звено по
свойствам будет приближаться к
интегрирующему и инерционному звеньям,
если τ > 1, то звено ближе к дифференцирующему
и инерционно-дифференциальному звеньям.

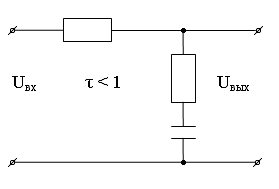
Переходя к изображениям при нулевых начальных условиях, имеем:
Передаточная функция:
 ,
,
Переходная функция:
 ,
,
 ,
,
Весовая функция:
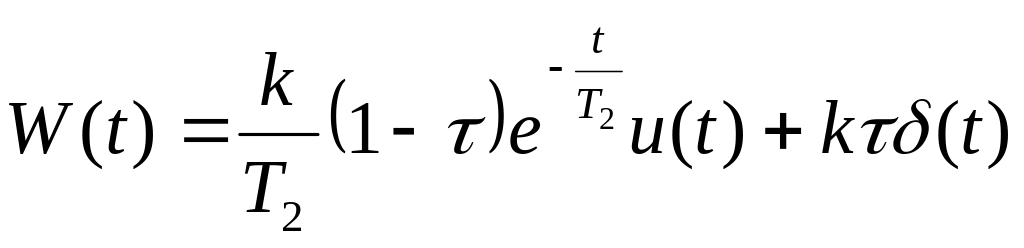 ,
,
Частотная характеристика:
 ,
где
,
где
Ω = ωТ2 – безразмерная частота,
АЧХ:
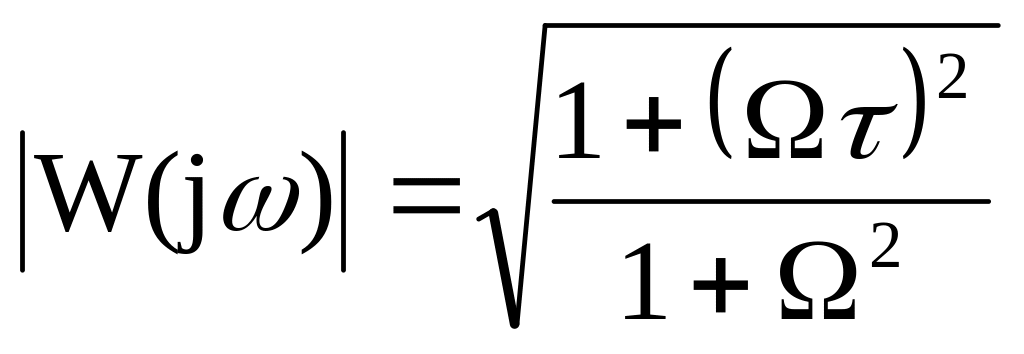 ,
,
ФЧХ:
 ,
,
ЛАЧХ:
 .
.

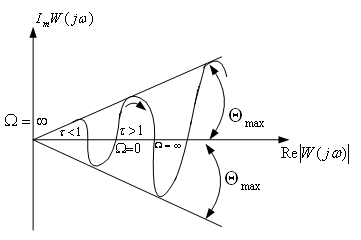


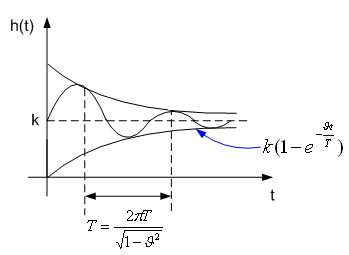
Колебательное звено.
Описывается дифференциальным уравнением второго порядка:
![]() при постоянной затухания
при постоянной затухания
![]() < 1
< 1
Требование < 1 вытекает из анализа решения этого уравнения:
![]()
Для нахождения решения следует разложить Y(p) на элементарные дроби, а затем восстановить оригинал:

Из выражения следует, что при
< 1 в системе наблюдается затухающие
гармонические колебания; при
>= 1 корни характеристического уравнения
![]() вещественны и колебания не возникают.
Если
= 1, то колебания будут незатухающими с
частотой
вещественны и колебания не возникают.
Если
= 1, то колебания будут незатухающими с
частотой
![]() .
.
Примеры: электрическая цепь, содержащая емкость, индуктивность и активное сопротивление; масса, подвешенная на пружине; маятник и др.
Переходя к изображениям при нулевых начальных условиях, имеем:
Передаточная функция:
 ,
,
Переходная функция:
 ,
,
 ,
,
Весовая функция:
 ,
,
Частотная характеристика:
 ,
,
Введем безразмерную частоту: Ω = ωТ
![]()
АЧХ:
 ,
,
ФЧХ:
 ,
,
ЛАЧХ:
 .
.
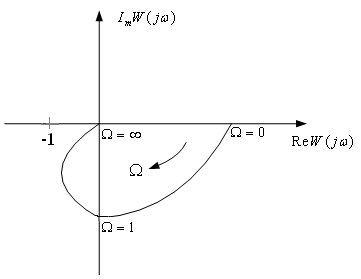
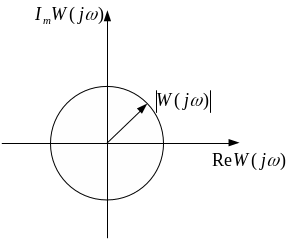
Как видно из рисунка годограф проходит
через 2 квадранта (III, IV)
и пересекает мнимую ось при Ω=1. Если
уменьшить, то петля, очерченная концом
вектора
![]() ,
увеличится.
,
увеличится.
![]()



Соединение звеньев и преобразование структурных схем линейных систем.
Звено в теории управления считается направленным, т.е. преобразует сигнал в одном направлении. Если ввести дополнительное предположение о независимости передаточных функций отдельных звеньев от их соединения, то каждая система может быть сведена к схеме, согласно которой:
![]() ,где
,где
![]() - управляемые величины и их составляющие,
зависящие от начальных условий.
- управляемые величины и их составляющие,
зависящие от начальных условий.
![]() - эквивалентная передаточная функция.
- эквивалентная передаточная функция.
На структурной схеме это уравнение выглядит следующим образом:

С математической точки зрения замена соединения нескольких звеньев одним звеном с эквивалентной передаточной функцией соответствует исключению переменных в системе уравнений.
Различают 3 вида соединения звеньев:
последовательное
параллельное
параллельное с обратной связью
Последовательным соединением звеньев называется такое соединение, когда выходная величина переднего звена является входной величиной последнего звена. Если последовательно соединяются звенья L и M:
 ,
то
,
то
Yl=Xm
В общем случае:

Последовательное соединение n звеньев с передаточными функциями Wi(p), где i = 1, 2, …, n может быть заменено звеном с эквивалентной передаточной функцией:
![]()
Переходя от передаточной функции к частотным характеристикам системы, т.е. полагая, что p = jω, получим^
![]()
Представив
![]() в виде
в виде
![]() получим:
получим:
![]() ,
,
![]()
Переходя к логарифму:
![]()
Таким образом, при последовательном соединении звеньев АЧХ перемножаются, а ЛАЧХ и ФЧХ складываются.
Параллельным соединением звеньев называют такое соединение, когда на входа всех элементов подается одна и та же величина, а выходные сигналы суммируются. Если параллельно соединены n звеньев, то входная величина х равна:
x = x1 = … = xn (1)
![]() (2)
(2)
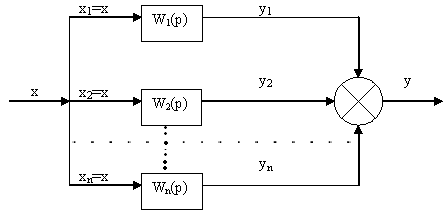
Переходя в (1) и (2) к изображениям и учитывая, что по определению передаточной функции:
![]() ,
,
получим:
![]() ,
,
т.е.:
![]() ,
,
и, следовательно:
![]() ,
,
![]() ,
,
т.е. при параллельном соединении звеньев переходная и весовая функции каждого звена суммируются.
Если комплексную передаточную функцию i-того звена представить как:
![]() ,
,
то эквивалентная комплексная передаточная функция:

Параллельное соединение с обратной связью.

![]()
![]()
![]()
![]()
![]()
Окончательно получим:
![]() .
.
![]()
![]()
![]()
Дифференциальное уравнение системы:
![]() .
.
Устойчивость линейных систем управления.
Каждая система управления характеризуется неким равновесным состоянием, которое нарушается при внешних воздействиях. Это могут быть помехи, сигналы управления и т.п.
Под устойчивостью систем подразумевается свойство системы возвращаться к первоначальному состоянию после прекращения воздействия выведшего систему из этого состояния.
Неустойчивая система не возвращается к состоянию равновесия по окончании воздействия, а непрерывно удаляется от него или совершает недопустимо большие колебания около него.
Различают устойчивости систем в «малом» и в «целом». Некоторые системы могут быть устойчивы при воздействиях, не выходящих за определенные пределы, и неустойчивы в целом при больших воздействиях.
Анализ корней характеристического уравнения показывает, что необходимым и достаточным условием устойчивости линейных систем является отрицательность вещественной части всех корней характеристического уравнения. Если среди его корней будет хотя бы одна пара комплексно-сопряженных корней с вещественной частью, равной нулю, то система будет совершать колебания с нарастающей амплитудой.
