Разбиение систем на звенья.

При построении функциональной схемы систем управления мы разбивали систему на элементы направленного действия в соответствии с функциями, которые они выполняют.

Для получения математического описания системы, её расчленяют на элементы направленного действия – звенья так, чтобы можно было сравнительно просто получить их математическое описание.

Звено – часть системы, которая осуществляет некоторое преобразование входной величины в выходную. В отличие, от функционального элемента, звено не обязательно конструктивно или схемно оформлено.

Если разбить систему на звенья направленного действия, то математическое описание каждого звена может быть выполнено без учета его связей с другими звеньями системы. При этом математическое описание всей системы может быть получено, как совокупность составленных независящих друг от друга уравнений звеньев системы и уравнений связи между ними.

Уравнения связи – уравнения, отражающие характер передачи воздействий между звеньями системы.

В результате разбиения системы на звенья, получается структурная схема системы.

Структурная схема системы – схема, показывающая, из каких звеньев состоит система, и как эти звенья соединены между собой.

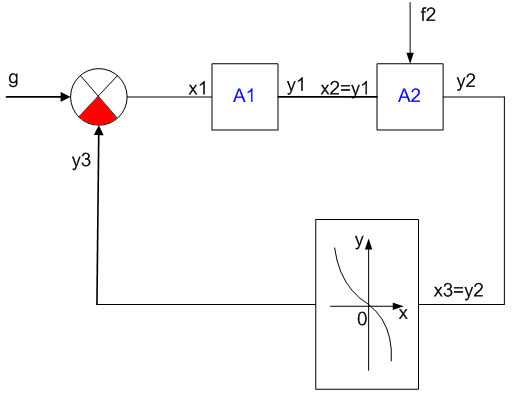
Схема состоит из 3-х звеньев. Зависимость между y₁ и х₁ задана выражением А₁. Зависимость между y₂ и х₂ – выражением А₂. Для третьего звена у₃ и х₃ – в виде графика.

Внешнее возмущающее воздействие на второе звено показано стрелкой f₂. ЭС (суммирующее звено), его выходная величина х₁=g – y₃.

Статические и динамические характеристики звеньев систем.

Уравнения звеньев систем составляются на основе тех физических законов, которые характеризуют их поведение (законы механики, электротехники, оптики и т.п.).

Уравнения, описывающие поведения звеньев, могут быть алгебраическими, дифференциальными и интегральными. Как правило, это дифференциальные уравнения.

Статическая характеристика звена представляет собой зависимость между входной x и выходной y величинами в установившемся режиме при различных постоянных значениях внешнего воздействия f (f(t)=f).

Рассмотрим пример звена – электродвигатель постоянного тока с независимым возмущением:

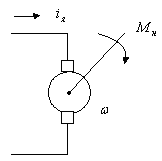
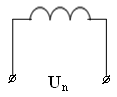
Входная величина – i_я, выходная величина – угловая скорость ω. Внешнее воздействие – момент нагрузки на валу М_н и напряжение питания обмотки независимого возбуждения U_п.

Один из многих возможных режимов работы двигателя, при котором U_п=М_н=const, называется номинальным. В этом режиме, как правило, рассчитывается работа двигателя.

При этих значениях и считается, что возмущение f = 0. В этом случае отклонения М_н и U_п от номинальных будут представлять из себя внешнее воздействие.

В документации на электродвигатель приводят статические характеристики, которые получают экспериментально при производстве двигателей при разных значениях момента нагрузки.

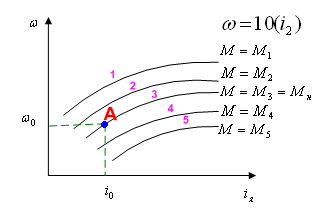
Точка А соответствует номинальному значению тока якоря i₀ и угловой скорости ω₀. При увеличении нагрузки на валу (М_н < М₀) статическая характеристика перемещается вниз (кривые 4, 5). При уменьшении нагрузки кривые ω(i_я) будут проходить выше (1, 2).

В общем случае зависимость установившегося значения выходной величины y от установившегося значения входной величины x является нелинейной.

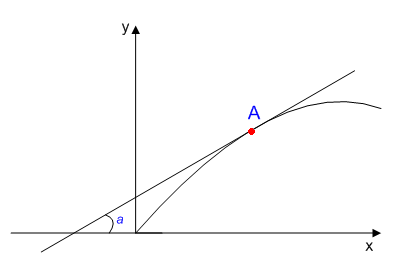
Угловой коэффициент, образуемый касательной к статической характеристике, в любой точке А называется коэффициентом усиления:

Из рисунка видно, что:

,

где r – масштабирующий коэффициент, зависящий от масштабов, принятых по осям x и y.

Значение коэффициента k₀ служит мерой астатизма звена. Если k₀ = ∞, то звено называется астатическим.

Астатическое звено при некотором значении входной величины x = x^* находится в равновесии при любом значении выходной величины y.

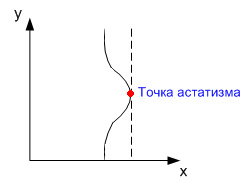
Если на находящееся в некотором состоянии звено подействует некоторое возмущающее воздействие, то оно начнет переходить в некоторое другое состояние. Характер процесса перехода системы из одного состояния в другое определяется динамической характеристикой звена (уравнением движения).

Уравнение движения звена – это уравнение (обычно дифференциальное), определяющее изменение во времени выходной величины звена по заданному изменению во времени его входной величины.

Дифференциальные уравнения могут быть разными для звеньев с сосредоточенными параметрами. Общее уравнение имеет вид:

F(y⁽ⁿ⁾, y^(n–1), …, ,у, x^(m), x^(m–1), …, , x, f^(g), f^(g-1), …, , f) = 0 (1)

Где m, n, g – натуральные числа, показывающие высший порядок производной от входной величины x, выходной y и внешнего воздействия f.

На практике, в большинстве случаев m < n, а g < n.

Например, при n = 1 уравнение звена имеет вид:

F( , y, x, f) = 0;

при n = 2:

F(y², , y, , x, , f) = 0.

Уравнение статической характеристики звена можно получить из уравнения (1), положив все производные по времени равными 0, т.е.:

F(0, 0, …, 0, y, 0, 0, …, 0, x, 0, 0, …, 0, f) = 0

Для линейных звеньев (описываемых линейными дифференциальными уравнениями) характерно, что реакция звена на линейную комбинацию воздействий равна той же линейной комбинации реакций звена на каждое влияние в отдельности. Это свойство линейных звеньев выражает собой принцип суперпозиции.

Т.к. решение нелинейных дифференциальных уравнений – задача значительно более сложная, то, когда это возможно, меняют нелинейные дифференциальные уравнения на приближенные линейные. Этот процесс называется линеаризацией.

Рис. 1

Если дифференциальное уравнение звена нелинейно из-за нелинейности его статических характеристик, то для линеаризации уравнения необходимо заменить нелинейную статическую характеристику y = ψ(x) на линейную характеристику y=ax + b.

Линеаризация осуществляется при помощи разложения в ряд Тейлора функции y = ψ(x). Это делается в окрестности некоторой точки (x₀, y₀) и отбрасыванием всех членов разложения, содержащих отклонение ∆y в степени, выше первой. Это означает замену кривой y = ψ(x) касательной в точке (x₀, y₀). В отдельных случаях линеаризация осуществляется путем проведения секущей между точками А и В (Рис.1).

Рассмотрим процесс линеаризации нелинейного уравнения звена при помощи разложения в ряд Тейлора на примере элемента, поведение которого описывается дифференциальным уравнением вида:

F(y^”, y^’, y, x,) = 0 (1)

Статическая характеристика такого звена описывается уравнением:

F(0, 0, y, x,) = 0

Если x₀, y₀ – некоторые установившиеся состояния, то координаты x и y можно записать в виде:

x = x₀ + ∆x;

y = y₀ + ∆y,

Где ∆x и ∆y – отклонения координат x и y от установившегося состояния.

Уравнение (1) в отклонениях имеет вид:

F(∆y^”, ∆y^’, y₀ + ∆y, x₀ + ∆x) = 0

Раскладывая левую часть уравнения в ряд Тейлора относительно точки установившегося состояния с координатами (0, 0, x, y), получим:

(2)

Индекс «0» означает, что производные берутся в точке x = x₀, y = y₀, из чего следует, что ∆x=∆y=0. Здесь в уравнении (2) не написаны члены, содержащие отклонения ∆x и ∆y в степени, выше первой. Частные производные в уравнении (2) – это числа, величина которых зависит от вида функции F(y^”, y^’, y, x,) = 0 и значений x₀ и y₀.

Полагая отклонения ∆x и ∆y и их производные по времени малыми, отбросим в уравнении (2) все члены, содержащие отклонения ∆x и ∆y, а также их производную в степени, выше первой, получим:

(3)

Уравнение (3) является линейным дифференциальным уравнением с постоянными коэффициентами I, II, III, IV.

Необходимым условием линеаризации является разложимость в ряд Тейлора функции:

.

Уравнение (3) приближенно заменяет уравнение (1) лишь в некоторой малой окрестности точки с координатами (0, 0, x, y). Величина этой окрестности зависит от вида функции , т.е. от величины производных порядка, выше первого в рассматриваемой точке. Линеаризованное уравнение обычно записывается в каноническом виде:

(4)

Линеаризация уравнения (1) при помощи разложения в ряд Тейлора означает замену поверхности, описываемой этим уравнением в пространстве переменных плоскостью касательной к поверхности точки с координатами 0, 0, y₀, x₀. Ошибка линеаризации тем меньше, чем меньше отклонение друг от друга точек поверхности (1) и точек плоскости (4).

Пример составления дифференциального уравнения звеньев систем управления.

Пример1: составим дифференциальное уравнение двигателя постоянного тока с независимым возбуждением и проведем его линеаризацию:

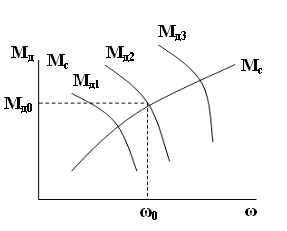
Рис.1.

М_с – момент сопротивления;

М_д – момент движения.

По второму закону Ньютона для вращательного движения уравнение для моментов на валу двигателя имеет вид:

, где (1)

ω – угловая скорость и момент инерции движущихся частей, приведенных к валу;

М_д – вращающий момент

М_с – момент сопротивления на валу двигателя.

М_д представляет из себя функцию двух переменных: скорости вращения и ????, а момент сопротивления функцию двух переменных (ω, t):

М_д = М_д(ω, u),

М_с = М_с(ω, t)

Т.к. М_д = М_д(ω, u) и М_с = М_с(ω, t) являются нелинейными функциями (см. рис.1), то уравнение (1) будет нелинейным дифференциальным уравнением.

Для линеаризации уравнения (1) перейдем к уравнению в отклонениях от установившегося режима, т.е. в точке, где М_с0 = М_д0. Пусть при этом ω = ω_0, а u = u₀. Разложим нелинейные функции М_д(ω, u), М_с(ω, t) в ряд Тейлора в окрестностях точки ω₀ и u₀ и отбросим члены, содержащие производные, выше первого порядка:

(2)

(3)

Подставив (2) и (3) в (1) получим:

(4)

В уравнении (4) все члены имеют размерность момента, однако часто бывает необходимо получить уравнение в относительных единицах с безразмерными коэффициентами или с коэффициентами размерности времени в степени, равной порядку соответствующей производной.

Разделим обе части уравнения на номинальное значение М_н:

Выберем некоторые величины переменных в качестве базисных.

Для напряжения u удобно взять максимальное значение u_мах, а для угловой скорости – её номинальное значение ω_н.

Умножив и разделив каждый член уравнения на соответствующую базисную величину, получим:

Введем обозначения:

Подставив эти коэффициенты в уравнение, получим:

Функция f(t) характеризует возмущающее воздействие, x(t) – управляющее воздействие, y(t) – выходную величину. Коэффициент Т имеет размерность времени (секунды) и называется постоянной времени двигателя.

Отношение k_y/k_c характеризует зависимость между выходной координатой y и входным воздействием x в установившемся режиме и называется коэффициентом усиления.

Пример2: получение дифференциального уравнения электрического пассивного четырехполюсника.

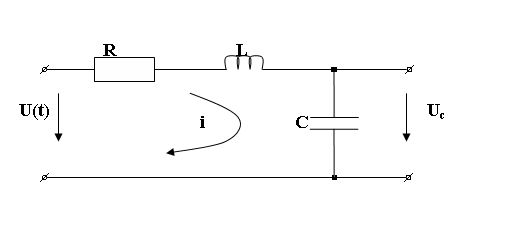
Входной характеристикой является напряжение на входных зажимах u(t), выходной – напряжение на конденсаторе u_с. Т.к. цепь является линейной (все элементы цепи линейные), уравнение можно составлять как в отклонениях, так и в безразмерных относительных единицах.

Падение напряжения на резисторе R:

,

Падение напряжения на индуктивности:

По второму закону Кирхгофа имеем, что приложенное напряжение – это его падение на всех элементах цепи:

Если обозначить U(t) = x; CL = ; RC = T₂, то тогда:

Составление дифференциальных уравнений систем автоматического управления.

Имея дифференциальные уравнения элементов системы и уравнения связи можно получить дифференциальные уравнения всей системы. Однако при исследовании систем управления обычно необходимо знать поведение выходной координаты системы, а не всех её элементов, поэтому можно от системы уравнений описывающих поведение элементов путем исключения промежуточных переменных перейти к одному уравнению. Это уравнение будет содержать только выходную координату системы, а также внешние воздействия. Зная внешнее воздействие, приложенное к системе, и решив дифференциальное уравнение, можно найти реакцию системы управления на эти воздействия. Пусть имеем уравнение объекта управления:

(1)

и уравнение управляющего устройства:

(2)

Запишем уравнение всей системы управления относительно ∆y. Для этого найдем из уравнения (1) величину ∆x, а также её производную:

Подставив значение ∆x и в уравнение (2), получим уравнение системы управления:

Таким образом, если объект управления и устройство управления описываются дифференциальными уравнениями первого порядка, то система управления в целом описывается дифференциальным уравнением второго порядка.

Пусть теперь объект управления описывается уравнением (1), а устройство управления – дифференциальным уравнением второго порядка:

(3)

Для получения дифференциального уравнения системы управления необходимо получить значение ∆x, а также первую и вторую производные от ∆x:

Подставив в уравнение (3) выражение для ∆x, и , получим искомое уравнение для всей системы в целом:

Полученное уравнение третьего порядка устанавливает связь между возмущающим воздействием f на систему и реакцией системы y.

Таким образом, для получения дифференциального уравнения системы, необходимо получить вначале дифференциальное уравнение для объекта управления и устройства управления; исключив из полученных уравнений промежуточные величины, можно получить дифференциальное уравнение относительно интересующих нас величин, но, как правило, эти преобразования очень трудоемки и громоздки.

Для того чтобы упростить решение данной и других задач, в теории автоматического управления вместо рассмотрения величин, характеризующих состояние во времени – оригиналов, рассматриваются соответствующие им изображения, полученные при помощи преобразований Лапласа.

Таким образом, при исследовании и расчетах систем управления широко используются операции исчисления, позволяющие существенно облегчить исследование сложных систем.

Операционное исчисление основывается на преобразованиях Лапласа и Фурье, которые позволяют заменять операции дифференцирования и интегрирования функций на операции более низкого ранга.

Линейные системы.

Система называется линейной, если уравнение динамики и, следовательно, статики этой системы линейны.

К линейным системам применим принцип суперпозиции, который формулируется следующим образом:

Пусть , где j = 1, 2, …, m – некоторые входные сигналы линейной системы, а – её реакция на каждый из сигналов, тогда для линейной системы суммарная реакция на суммарный входной сигнал равна:

Передаточная функция линейной системы.

Линейные системы в общем случае могут быть описаны дифференциальным уравнением с постоянными коэффициентами вида:

Используя свойство (3), дифференцирование оригинала, к обеим частям уравнения получим:

При нулевых начальных условиях найдем связь между лапласовскими изображениями системы y(t) и входного воздействия на систему x(t), получим:

Функция представляющая собой отношение изображения выходного сигнала линейной системы к изображению входного сигнала при нулевых начальных условиях, называется передаточной функцией линейной системы.

Смысл передаточной функции заключается в том, что она представляет собой некий оператор, преобразующий внешнее воздействие на входе в реакцию системы на выходе, т.е.:

Таким образом, любой линейный объект может быть представлен следующим образом:

В случае, если система управления является замкнутой (охваченной обратной связью), то передаточная функция определяется как:

, где (2)

W_об.св.(p) – передаточная функция управляющего устройства,

Знак «+» - соответствует отрицательной обратной связи, а «-», наоборот.

Формула (2) получается из следующих соображений:

по определению передаточной функции имеем:

, но

передаточная функция объекта управления:

, а

передаточная функция звена обратной связи:

Как видно из рисунка:

, т.е.

,

разделив числитель и знаменатель на X₂(p) получим:

Переходная функция.

Сигнал h(t), полученный на выходе системы при подаче на её вход единичного скачка u(t), называется переходной функцией системы.

Известно, что изображением единичного скачка является:

и, следовательно,

по определению передаточной функции:

.

Связь между передаточной и переходной функцией находиться из формулы:

при x(t) = u(t) получим:

Отсюда имеем:

, отсюда видно, что

оригинал передаточной функции равен производной от переходной функции.

Реакция системы y(t) на произвольное входное воздействие x(t), выраженное через переходную функцию h(t) имеет вид:

Весовая или импульсная переходная функции системы.

Рассмотрим функцию δ(t), называемую функцией Дирака. В теории управления её называют единичным импульсом. Определим δ(t):

∞, при t = 0

δ(t) =

0, при t ≠ 0

или

В общем случае, как и функция Хевисайда, функция Дирака является математической абстракцией.

Рассмотрим вспомогательную функцию δ(t, μ):

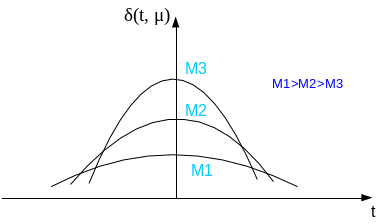
В этом случае функцию δ(t) можно рассматривать как предел функции δ(t,μ) при μ → ∞, т.е.

∞, при t = 0

0, при t ≠ 0

Если воспользоваться формальным равенством, то по определению производной получим:

Исходя из формального равенства и того, что получим:

.

Сигнал, получаемый на выходе линейной системы при подаче на её вход единичного импульса, называется весовой или импульсной переходной функцией. И так как изображение входного сигнала , то по определению передаточной функции:

Y(p) = W(p),

т.е., переходя от изображения к оригиналу:

получаем оригинал передаточной функции.

Частотные и логарифмические характеристики линейных систем.

Частотной характеристикой линейной системы или комплексно- частотной функцией линейной системы называется функция W(jω), получаемая из передаточной функции системы подстановкой p = jω.

Физически эта подстановка означает, что сигнал на входе системы является синусоидальным (гармоническим). Частотную характеристику можно представить в виде:

(1)

Где R(ω) и I(ω) вещественная и мнимая части комплексно-частотной характеристики соответственно.

Формула (1) показывает, что W(jω) является векторной суммой R(ω) и I(ω) в декартовых координатах на комплексной плоскости. В полярных координатах:

(2),

где

Функции W(ω) и Θ(ω) определяют изменение амплитуды и фазы колебаний на выходе по отношению к амплитуде и фазе колебаний на входе и называются АЧХ и ФЧХ соответственно.

Рассматривая W(jω) как вектор и варьируя частоту входного сигнала ω от 0 до ∞, получаем на комплексной плоскости кривую, описываемую концом этого вектора. Эта кривая называется годографом вектора комплексно- частотной функции или амплитудно-фазовой частотной характеристикой (АФЧХ).

Заметим, что

jI(ω)

R(ω)

Широкое практическое применение нашли частотные характеристики, построенные в логарифмическом масштабе.

Логарифмируя выражение (2) получаем:

Зависимость называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ), а Θ = Θ(lgω) – логарифмической фазо-частотной характеристикой (ЛФЧХ).

ЛАЧХ и ЛФЧХ строятся в логарифмическом масштабе, т.е. по оси абсцисс откладываются логарифмические частоты.

За единицу масштаба принимается декада – это частотный интервал, соответствующий изменению частоты в 10 раз.

По оси ординат при построении ЛФЧХ фаза откладывается в радианах или угловых градусах.