IV. Оценка качества регулирования нелинейной сау температуры.

4.1 Исследуем переходный процесс в САУ температуры аналитическим методом.

Построим диаграммы качества переходного процесса по коэффициенту условия разомкнутой системы при отключенной местной обратной связи ( ).

Согласно структурно-математической схеме (см. рис. 3) передаточная функция гармонически линеаризованной разомкнутой системы равна:

(4.1.1)

где

- коэффициент гармонической линеаризации для релейной характеристики с зоной нечувствительности.

По передаточной функции (4.1.1) определяем характеристический полином замкнутой нелинейной системы

Для построения диаграммы качества в полиноме (4.1.2) произведем подстановку ( – показатель затухания). Эту подстановку удобно выполнять путем разложения полинома в ряд по степеням jω:

(4.1.3)

где индекс ξ означает, что в выражения для производных необходимо подставить ξ вместо p.

Из (4.1.2) находим

(4.1.4)

Подставим выражения (4.1.4) в ряд (4.1.3), выделим в последнем вещественную и мнимую часть и приравняем их к нулю. Получим

(4.1.5)

Из второго уравнения (4.1.6) находим ω = 0. Подставим это значение в первое уравнение системы (4.1.5) и решим его относительно k:

(4.1.6)

В выражение (4.1.6) подставим численные значения параметров. Получим:

(4.1.7)

Задаемся различными значениями амплитуды колебаний а и при выбранных постоянных значениях показателя затухания ξ строим кривые а а(k) (см.рис. 10). Кривые ξ > 0 соответствуют расходящимся колебаниям, а кривые ξ < 0 – затухающим колебаниям. Область, лежащая правее штриховой прямой, проходящей через точку k, является областью существования автоколебаний. Область, расположенная левее этой прямой, является областью устойчивого равновесного состояния системы.

Как видно из анализа графиков на рис. 10, все кривые, построенные при ξ < 0 (-0,1 < ξ < 0) для того, чтобы коэффициент усиления k был положительным, расположены левее прямой, проходящей через точку k ≈ 0,005. Следовательно, САУ температуры находится в устойчивом равновесном состоянии.

Рис. 10. Диаграмма качества переходного процесса в САУ температуры

4.2 Исследуем переходный процесс в САУ температуры частотным методом.

Коэффициент затухания ξ и частоту колебаний ω переходного процесса в САУ температуры будем отыскивать путем решения гармонически линеаризованного уравнения

(4.2.1)

или

(4.2.2)

где получается из передаточной функции линейной части системы подстановкой , а гармонически линеаризованная передаточная функция нелинейного звена – подстановкой в выражение

(4.2.3)

в результате которой получаем

(4.2.4)

Уравнение (4.2.1) будем решать графически. Для этого в передаточной функции линейной части системы

(4.2.5)

произведем подстановку . Получим

(4.2.6)

Модуль этой функции

(4.2.7)

и фаз

(4.2.8)

Подставив в выражение (4.2.7) и (4.2.8) приведенные в исходных данных значения параметров и, задаваясь различными постоянными значениями показателя затухания ξ, построим серию кривых как функции от частоты колебаний ω при ξ = const (см. рис. 11).

На этом же графике нанесем обратную амплитудно-фазовую характеристику нелинейного звена при заданных параметрах b и c. Для нелинейной характеристики релейного типа с зоной нечувствительности имеем

(4.2.9)

Отсюда

(4.2.10)

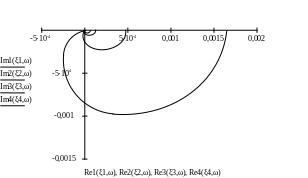
Рис. 11. Частотные характеристики линейной части системы и нелинейного звена САУ температуры

Как видно из графиков, точка пересечения годографов линейной части системы и нелинейного звена отсутствует. Следовательно, САУ температуры находится в устойчивом равновесном состоянии.