1.Гамма-функция

Рассмотрим несобственный интеграл

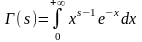(1)

как функцию от s и выясним область ее определения. Для этого представим интеграл (1) в виде суммы несобственных интегралов

.

Поскольку для всех и всех , а эталонный интеграл сходится при ; т.е. при , и расходится при , то, по признакам сравнения несобственных интегралов, интеграл сходится при всех и расходится при .

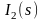Поскольку для любого и сходится, то по аналогичному признаку сравнения заключаем, что несобственный интеграл сходится при всех .

Окончательно, несобственный интеграл (1) сходится только при ; т.е. областью определения гамма-функции Г(s) служит множество всех положительных чисел.

Интегрируя по частям (подстановка верхнего предела означает переход ),

. (2)

Формула , задает функциональное уравнение для гамма-функции.

Покажем, что при , где n-натуральное число, ; т.е. гамма-функция есть обобщение понятия факториала. При

.

При , где n-натуральное число большее 1, пользуемся функциональным уравнением

.

Положив 0!=1, получим, что равенство выполняется для всех натуральных чисел.

Известно, что гамма-функция Эйлера бесконечно дифференцируема на , выпукла вниз и её минимум приходится в точке интервала , поскольку .

2. Бета-функция

Эйлером предложен также несобственный интеграл

(3)

как функция параметров , которую называют бета-функцией. Представим интеграл (3) в виде суммы двух слагаемых

,

где имеет особенность только в точке , а - только в точке .

Поскольку для любого функция положительна, непрерывна и ограничена на отрезке , то существуют постоянные , что для всех и всех . Поэтому, как и в предыдущем пункте, убеждаемся, что интеграл сходится для всех только при .

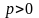Аналогично, функция положительна, непрерывна и ограничена на отрезке 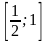для любого , и, следовательно, существуют , что для всех и всех .

Поэтому несобственный интеграл сходится для каждого только при .

Окончательно, бета-функция 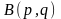определена только для и .

Совершая в интеграле (3) замену переменной интегрирования , получим

. (4)

Формула (4) указывает на свойство симметричности бета-функции Эйлера.

Интегрируя в (3) по частям и используя разложение 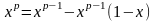, получим

откуда

(5)

В силу симметричности функции имеем также

(5’)

Формулы (5) и (5’) называют функциональными уравнениями для бета-функции.

Если то согласно (5)

Но

Так что

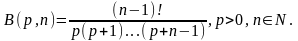(6)

Если то (6) принимает вид

Так как то мы доказали частный случай

замечательной формулы Эйлера

Гамма-функция и бета-функция, как и экспоненциальная функция, играют фундаментальную роль в математике и её приложениях.

Сформулируем без доказательств несколько полезных свойств этих функций:

Для любого ,

Из этого, в частности, следует, что

и, следовательно,

Бета-функция допускает ещё представление в виде интеграла

Часто используется интеграл (вы встретите его при вычислении двойных, тройных интегралов при переходе к сферическим или цилиндрическим координатам)

Сведём его к значениям эйлеровых интегралов: