Правило трех сигм

На практике достаточно часто требуется оценить вероятность того, что отклонение нормально распределенной величины Х по абсолютному значению не превышает определенный размер, который обычно принимается равным положительному числу δ.

Другими словами, требуется найти вероятность того, что осуществляется неравенство |Х-а| < δ.

Это неравенство равносильно следующему: -δ < Х-а < δ или (а- δ)< Х< (а+ δ).

Используя правило, что вероятность попадания нормально распределенной случайной величины в заданный интервал равна разнице значений функции Лапласа на границах этого интервала, т.е Р(α< Х < β)= =Ф( ) - Ф( )=2Ф, получим:

Р(|Х-а| < δ)= Р((а- δ)< Х< (а+ δ))= Ф [ ] - Ф[ ]=Ф( ) – Ф( )=2Ф( ).При а=0, получим Р(|Х|)< δ)=2Ф( ).. . . .(5.32).

Если положить, что δ=3σ, получим Р(|Х-а| <3σ)=2Ф(3)=2·0,49865=0,9973.

Таким образом, вероятность отклонения истинного значения случайной величины Х по абсолютному значению будет меньше утроенного значения среднего квадратического отклонения равна 0,9973. Это и есть правило трех сигм.

Формулируется оно следующим образом:

Если случайная величина распределена нормально, то абсолютная величина ее максимального отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Это правило применимо и следующим образом: если распределение случайной величины неизвестно, но условие указанное в правиле трех сигм соблюдается, то есть основание предполагать, что изучаемая случайная величина распределена нормально, в противном случае – нет.

Контрольные вопросы

1. Дифференциальная функция распределения результатов измерений и случайной погрешности, подчиняющаяся нормальному закону. Аналитическая зависимость, графический вид, начальный и центральные моменты.

2. Интегральная функция, соответствующая нормальному закону распределения.

3. Правило трех сигм.

5.5.2. Равномерный закон распределения.

Равномерным распределением называют такое распределение случайной величины, при котором она может принимать любое значение в заданных пределах с одинаковой вероятностью.

Дифференциальная функция равномерного распределения случайной величины (плотность вероятности) представлена на рис. 5.11.

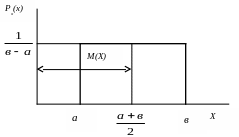
Рис. 5.11

Представленные на рис. 5.11 параметры «а» и «в» определяют пределы изменения случайной величины Х.

Область определения плотности вероятности или дифференциальной функции равномерного распределения следующая:

 0, если -  Х  а

Р_х =  , если а  Х  в. . . . . (5.33).

 0, если в X  +

Интегральная функция равномерного закона распределения для а  Х  в выглядит следующим

образом:

F(X)= , при а Х  в. . . (5.34).

Числовые характеристики моментов равномерного распределения случайной погрешности следующие:

М =0 - математическое ожидание . . . . . .(5.35),

D = - дисперсия . . . . . . . . . . . . . . . . . .. . . . .(5.36),

= - среднее квадратичное отклонение. . . . . .(5.37),

_k=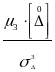 =0 -коэффициент асимметрии . . . . . . . . (5.38),

Е_х= -3=-1,2 - эксцесс. . . . . . . . . . . . . . . . (5.39).

Практически предельное поле рассеивания при равномерном распределении равно (в-а), т.е. оно равно 2 .

Г

F(X)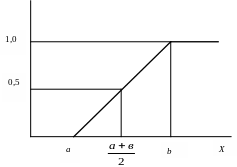

рафик интегральной функции равномерного распределения представлен на рис. 3.25.

Рис. 5.12