2.3. Формулы для коэффициентов регрессии. Обязательные свойства линии регрессии. Недостатки метода наименьших квадратов
После построения линии регрессии более детально рассмотрим общее выражение для остатка в каждом наблюдении. Логика этого рассмотрения является достаточно простой. Однако на первый взгляд она может показаться абстрактной, поэтому полезно графическое представление.
*
P
* R
а *S
a
T
x
Рис. 2.4 Линия регрессии, построенная по выборке наблюдений
На рис. 2.4 линия регрессии = а + bх построена по выборке наблюдений. Для того чтобы не загромождать график, показано только одно такое наблюдение: наблюдение i, представленное точкой Р с координатами (x , у ).
Когда
х =х
линия регрессии предсказывает значение
у =
,
что соответствует точке R
на графике, где
= а+bх . (2.2)
Используя условные обозначения, принятые на рис. 2.4, это уравнение можно переписать следующим образом:
RT=ST+RS, (2.3)
так как отрезок ST равен а, а отрезок RS равен bх .
Остаток PR — это разность между РТ и RT:
PR = PT – RT = PT – ST - RS. (2.4)
Используя обычную математическую запись, представим формулу (2.4) в следующем виде:
=
у
-
=
у
-
а- bх
(2.5)
Если бы в примере, показанном на графике, мы выбрали несколько большее значение а или несколько большее значение b, то прямая прошла бы ближе Р, и остаток е был бы меньше. Однако это повлияло бы на остатки всех других наблюдений, и это необходимо учитывать. Минимизируя сумму квадратов остатков, мы попытаемся найти некоторые равновесия между ними.
Рассмотрим случай, когда имеется n наблюдений двух переменных х и у. Предположив, что у зависит от х, мы хотим подобрать уравнение
= а + bх (2.6)
Таким образом, МНК, примененный к модели парной регрессии у = а + bх + u, дает следующие оценки параметров регрессии:
(2.7)
Подставив
это выражение для оценки а в исходное
уравнение регрессии у = а + bх, получим у
-
= b(х -
). Откуда следует, что линия регрессии
всегда проходит через точку (
,
).
Рассмотрим вывод выражений для а и b.
Расчетное
значение зависимой переменной
,
и остаток
для наблюдения i
заданы уравнениями (2.2) и (2.5). Мы хотим
выбрать а и b, чтобы минимизировать
величину S:
S
=
(2.8)
Можно обнаружить, что величина S минимальна, когда
b
=
(2.9)
a = у – bx (2.9')
Вывод выражений для а и b будет осуществляться в соответствии с той же процедурой, которая использовалась в двух примерах в разделе 2.3, и предлагается сравнивать общий вариант с примерами на каждом этапе. Начнем с того, что выразим квадрат i-го остатка через а и наблюдения значений х и у;
(2.10)
Суммируя по всем n наблюдениям, запишем S в виде
S=
(2.11)
Заметим, что данное выражение для S является квадратичной функцией от а и b, и ее коэффициенты определяются выборочными значениями х и у. Мы можем влиять на величину S, только задавая значения а и b. Значения х и у, которые определяют положение точек на диаграмме рассеяния, уже не могут быть изменены после того, как мы взяли определенную выборку. Полученное уравнение представляет собой обобщенный вариант уравнений (2.2) и (2.13).
Условия
первого порядка для минимума, то есть
= 0, принимают вид:
(2.12)
(2.13)
Эти
уравнения известны как нормальные
уравнения для коэффициентов регрессии.
Уравнение (2.12) позволяет выразить a через
и пока неизвестное b. Подставив n
вместо
,
и их вместо
,
получим:
(2.14)
Следовательно,
(2.15)
Подставив
выражение для а в уравнение (2.13) и помня,
что
,
равно n
,
имеем:
(2.16)
После деления на 2n и перегруппировки получим:
(2.17)
Это выражение можно переписать в следующем виде:
bVar (x) = Cov (x,y) (2.18)
и, таким образом, мы получим уравнение (2.9). Найдя из этого выражения b, выразим затем а из уравнения (2.9') Тот, кто знаком с условиями второго порядка, без труда сможет убедиться, что они удовлетворены.
Существуют два этапа интерпретации уравнения регрессии. Первый этап состоит в словесном истолковании уравнения так, чтобы это было понятно человеку, не являющемуся специалистом в области статистики. На втором этапе необходимо решить, следует ли ограничиться этим или провести более детальное исследование зависимости.
Оба этапа чрезвычайно важны. Второй этап мы рассмотрим несколько позже, а пока обратим основное внимание на первый этап. Это будет проиллюстрировано с помощью функции спроса, оцененной как регрессия между расходами потребителей на питание (у) и располагаемым личным доходом (х) по данным США за период с 1959 по 1983 гг. Данные представлены в виде графика (рис. 2.5).
Предположим, что истинная модель описывается следующим выражением:
,
(2.21)
и оценена регрессия
у = 55,3+0,093х. (2.22)
Полученный результат можно истолковать следующим образом. Коэффициент при х (коэффициент наклона) показывает, что если х увеличивается на одну единицу, то у возрастает на 0,093 единицы. Как х, так и y измеряются в миллиардах долларов в постоянных ценах; таким образом, коэффициент наклона показывает, что если доход увеличивается на 1 млрд. долл., то расходы на питание возрастают на 93 млн. долл. Другими словами, из каждого дополнительного доллара дохода 9,3 цента будут израсходованы на питание.
Что можно сказать о постоянной в уравнении? Формально говоря, она показывает прогнозируемый уровень, когда х = 0. Иногда это имеет ясный смысл, иногда нет. Если х = 0 находится достаточно далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам; даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантии, что так же будет при экстраполяции влево или вправо.
р асходы на питание
y
150
*
*
100 *
*
*
*
50
x
0 200 400 600 800 1000 1200 доход
Рис.2.5 Регрессивная зависимость расходов на питание от доходов
В рассматриваемом случае экстраполяция к вертикальной оси приводит к выводу о том, что если доход был бы равен нулю, то расходы на питание составили бы 55,3 млрд. долл. Такое толкование может быть правдоподобным в отношении отдельного человека, так как он может израсходовать на питание накопленные или одолженные средства. Однако оно не имеет никакого смысла применительно к совокупности. В данном случае константа выполняет единственную функцию: она позволяет определить положение линии регрессии на графике.
При интерпретации уравнения регрессии чрезвычайно важно помнить о трех вещах. Во-первых, a является лишь оценкой , a b - оценкой . Поэтому вся интерпретация в действительности представляет собой лишь оценку. Во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. В-третьих, верность интерпретации зависит от правильности спецификации уравнения.
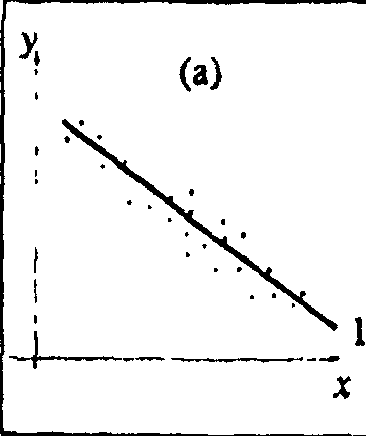
Рис.2.6 Три варианта соотношения линии линейной регрессии и реальных данных
"Наилучшая" по МНК прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость y = f(x) является, например, квадратичной (как на рисунке 2.6.6), то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется наилучшая. Если величины х и у вообще не связаны (рис. 2.6,с), мы также всегда сможем найти "наилучшую" линейную функцию у = а + bх для данной совокупности наблюдений, но в этом случае конкретные значения а и b определяются только случайными отклонениями переменных и сами будут очень сильно меняться для различных выборок из одной и той же генеральной совокупности. Возможно, на рис 26, с прямая 1 является наилучшей среди всех прямых линий (в смысле минимального значения функции Q), но любая другая прямая проходящая через центральную точку "облака" (например, линия 2) ненамного в этом смысле хуже, чем прямая 1, и может стать наилучшей в результате небольшого изменения выборки.