Результаты расчетов стандартных ошибок

Эксперимент	С.о.(b)	Эксперимент	С.о.(b)
1	0.043	6	0.044
2	0.041	7	0.039
3	0.038	8	0.040
4	0.035	9	0.033
5	0.027	10	0.033

где y – результат очередной игры, x – число игр, проведенных игроком до текущей игры (порядковый номер текущей игры минус единица), и u – случайный член. Как видите, большинство оценок достаточно хороши.

В следующей таблице приведены результаты первых 20 игр нового игрока, x автоматически изменяется от 0-19, в качестве значений u были взяты числа, полученные с помощью генератора нормально распределенных случайных чисел с нулевым средним и единичной дисперсией, которые были затем умножены на 400; величина определялась через значения x и y в соответствии с линейной кривой обучения.

Таблица 3.6

Результаты расчетов

Наблюдение	x	u	y	Наблюдение	x	u	y
1	0	-236	264	11	10	636	2136
2	1	-96	504	12	11	-368	1232
3	2	-332	368	13	12	-284	1416
4	3	12	812	14	13	-100	1700
5	4	-152	748	15	14	676	2576
6	5	-876	124	16	15	60	2060
7	6	412	1512	17	16	8	2108
8	7	96	1296	18	17	-44	2156
9	8	1012	2312	19	18	-364	1936
10	9	-52	1348	20	19	-568	2968

Оценивая регрессию между y и x, получим уравнение (в скобках указаны стандартные ошибки):

4. Проверка гипотез

4.1. Выбор нулевой и альтернативной гипотезы

В статистическом исследовании теория и практика взаимно обогащают друг друга и вопрос о том, что первично: теоретическое построение гипотез или эмпирический анализ не стоит.

Поэтому вопрос о проверке гипотез мы будем рассматривать с двух точек зрения. С одной стороны, мы можем предположить, что сначала формулируется гипотеза, и цель эксперимента заключается в выяснении ее применимости. Это приведет к проверке гипотезы о значимости. С другой стороны, мы можем сначала провести эксперимент и затем определить, какие из теоретических гипотез соответствуют результатам эксперимента. Это приведет к построению доверительных интервалов.

Если вам известна логика, лежащая в основе построения критериев значимости и доверительных интервалов, вы уже знакомы с большинством понятий, используемых в регрессионном анализе. Однако один большой вопрос может оказаться новым – это использование односторонних критериев. Такие критерии применяются в регрессионном анализе очень часто. Поэтому важно понять целесообразность их применения, и путь к этому лежит через последовательный ряд небольших аналитических шагов.

Формулирование нулевой гипотезы

Начнем с допущения о том, что формулирование гипотезы предшествует эксперименту и что вы уже имеете в виду некоторую гипотетическую связь или зависимость. Например, можно считать, что темпы общей инфляции в экономике (p, в процентах) зависят от темпов инфляции, вызванной ростом заработной платы (w, в процентах), и что эта зависимость описывается линейным уравнением:

(4.1)

где и - параметры, а u – случайный член. Далее можно построить гипотезу о том, что без учета эффектов, вносимых случайным членом, общая инфляция равна инфляции, вызванной ростом заработной платы. В этих условиях можно сказать, что гипотеза, которую вы собираетесь проверить, считается нулевой, обозначается , состоит в том, что при . Мы так же определяем альтернативную гипотезу, которая обозначатся , и представляет собой заключение, даваемое в том случае, если экспериментальная проверка указала на ложность . В данном случае эта гипотеза состоит в том, что . Две гипотезы сформулированы с использованием следующих обозначений:

_{: ;}

_{: .}

В этом конкретном случае, если действительно считать, что общая инфляция равна инфляции, вызванной ростом заработной платы, мы не делаем попыток защитить нулевую гипотезу , подвергнув ее максимально строгой проверке надеясь, что она не будет опровегнута. Однако на практике более обычным является построение нулевой гипотезы, которая предполагается верной. Например, рассмотрим простую функцию спроса:

, (4.2)

где - величина спроса, скажем, на продукты питания, а - доход.

Исходя из вполне разумных теоретических оснований, вы предполагаете, что спрос на продукты питания зависит от дохода, но ваша гипотеза недостаточно “сильна”, чтобы можно было определить конкретное значение для . Тем не менее вы можете установить наличие зависимости величины от , используя для этого обратную процедуру, когда в качестве нулевой гипотезы принимается утверждение о том, что величина не зависит от , т.е. что . Альтернативная гипотеза заключается в том, что , иными словами, что значение влияет на величину . Если можно отвергнуть нулевую гипотезу, вы таким образом устанавливаете наличие зависимости, по крайней мере в общих чертах. С использованием введенной системы обозначений нулевая и альтернативная гипотезы соответственно примут вид:

: и : .

Обобщив сказанное, введем определения.

Нулевая гипотеза ( ) – утверждение о том что, неизвестный параметр модели принадлежит заданному множеству А.

Альтернативная гипотеза – утверждение о том, что неизвестный праматр модели принадлежит другому заданному множеству В, .

Последующее рассмотрение касается модели парной регрессии (3.1). Оно будет относиться только к коэффициенту наклона , но точно такие же процедуры применены и к постоянному члену . Возьмем общий случай, в котором в нулевой гипотезе утверждается, что равно некоторому конкретному значению, скажем, , и альтернативная гипотеза состоит в том, что не равно этому значению ( : и : ). Вы можете предпринять попытку отклонить или подтвердить нулевую гипотезу в зависимости от того, что вам необходимо в данном случае. Будем предполагать, что четыре условия Гаусса- Маркова выполняются.

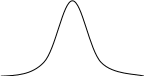
Если гипотеза верна, то оценки , полученные в ходе регрессионного анализа, будут иметь распределение с математическим ожиданием и дисперсией /[nVar(x)] [см. уравнение (3.28)]. Теперь мы вводим допущение, что остаточный член u имеетнормальное распределение. Если это так, то величина будет также нормально распределена, как показано на рис 4.1.

Функция плотности

Вероятности для b

b

Рис. 4.1 Структура нормального распределения оценки b, выраженной через стандартные отклонения от математического ожидания

Сокращение "с.о." на рисунке соответствует величине стандартного отклонения оценки , т.е. . Учитывая структуру нормального распределения, большинство оценок параметра будет находиться в пределах двух стандартных отклонений от (если верна гипотеза ).

Сначала мы допустим, что знаем значение стандартного отклонения величины . Это нереалистичное допущение, и мы позднее отбросим его. На практике же значение этого отклонения (также как и неизвестные значения параметров и ) подлежит оценке. Можно тем не менее упростить рассмотрение, предположив, что точное значение отклонения известно, и, следовательно, имеется возможность построить график (рис.3.4).

Проиллюстрируем это на примере модели общей инфляции (3.34). Предположим, что некоторым образом мы знаем, что стандартное отклонение величины составляет 0,1. Тогда, если нулевая гипотеза , то оценки коэффициентов регрессии будут распределены так, как это показано на рис. 3.5. Из этого рисунка можно видеть, что при справедливости нулевой гипотезы оценки будут находиться приблизительно между 0,8 и 1,2.