Результаты оценки значений a и b

Эксперимент
1	1,26	0.58
2	3,05	0,45
3	2,26	0,39
4	2,28	0,50
5	1,42	0,61
6	1,61	0.52
7	1,44	0,63
8	4,37	0,33
9	0,52	0,65
10	1,88	0,55

В табл. 3.4 приведены результаты всех 10 экспериментов при . Мы будем называть это серией экспериментов II, а первоначальную серию экспериментов, результаты которых приведены в табл. 3.2, — серией I. При сравнении табл. 3.2 и 3.4 можно видеть, что значения и во второй таблице являются значительно более неустойчивыми, хотя в них по-прежнему нет систематической тенденции к занижению или завышению значений оценок.

Детальное исследование позволяет обнаружить важную особенность. В серии I значение в эксперименте было равно 0,54, и завышение оценки составило 0,04. В серии II значение в эксперименте равнялось 0,58 и завышение составило 0,08, т.е.: оно было ровно вдвое больше, чем раньше. То же самое повторяется для каждого из 9 другиx экспериментов, а также для коэффициента регрессии а в каждом эксперименте. Удвоение случайного члена в каждом наблюдении приводит к удвоению ошибок в значениях коэффициентов регрессии.

Этот результат следует непосредственно из разложения b в соответствии с уравнением (3.6). В серии I случайная ошибка в b задается в виде . В серии II она представлена как , и

(3.11)

Увеличение неточности отражено в функции плотности вероятности для b в серии II, показанной на рис. 3.2, Эта функция вновь симметрична относительно истинного значения 0,50, однако если вы сравните ее с функцией, изображенной на рис, 3.1, то увидите, что данная кривая более полога и широка. Удвоение значений и привело к удвоению стандартного отклонения распределения.

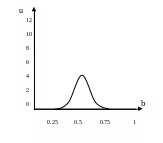
Рис. 3.2 Распределение b при удвоении стандартного отклонения u

Итак, очевидно, что свойства коэффициентов регрессии существенным образом зависят от свойств случайной составляющей. В самом деле, для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, случайный член должен удовлетворять четырем условиям, известным как условия Гаусса - Маркова. Не будет преувеличением сказать, что именно понимание важности этих условий отличает компетентного исследователя, использующего регрессионный анализ, от некомпетентного. Если эти условия не выполнены, исследо­ватель должен это сознавать. Если корректирующие действия возможны, то аналитик должен быть в состоянии их выполнить. Если ситуацию исправить невозможно, исследователь должен быть способен оценить, насколько серьезно это может повлиять на результаты.

Условия Гаусса - Маркова для модели парной регрессии:

1) случайный член регрессии в каждом наблюдении имеет нулевое Математическое ожидание: М( ) = 0 для любого i.

2) дисперсия случайного члена регрессии не зависит от номера наблюдения: - не зависит от i.

3) случайные члены регрессии в разных наблюдениях не зависят друг от друга: i=j

4) случайный член регрессии и объясняющая переменная в каждом наблюдении независимы друг от друга: для любого k.

Рассмотрим теперь эти условия одно за другим, объясняя кратко, почему они имеют важное значение. Три последних условия будут также Подробно рассмотрены в следующих главах.

1 -е условие Гаусса - Маркова: М(и) =0 для всех наблюдений

Первое условие состоит в том, что математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематическое смещение ни в одном из двух возможных направлений.

Фактически если уравнение регрессии включает постоянный член, то обычно бывает разумно предположить, что это условие выполняется автоматически, так как роль константы состоит в определении любой систематической тенденции в у, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

2-е условие Гаусса - Маркова: постоянна для всех наблюдений

Второе условие состоит в том, что дисперсия случайного члена должна был постоянна для всех наблюдений. Иногда случайный член будет больше, иногда меньше, однако не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других.

для всех i, (3.12)

Так как и , условие можно переписать в виде:

для всех i. (3.13)

Величина , конечно, неизвестна. Одна из задач регрессионного

анализ состоит в оценке стандартного отклонения случайного члена.

Если рассматриваемое условие не выполняется, то коэффициенты регрессии, найденные по обычному методу наименьших квадратов, будут неэффективны, и можно получить более надежные результаты путем применения модифицированного метода регрессии. Это будет рассмотрено в главе 7.

3-е условие Гаусса - Маркова:

Это условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Например, если случайный член велик и положителен в одном наблюдении, это не должно обусловливать систематическую тенденцию к тому, что он будет большим и положительным в следующем наблюдении (или большим и отрицательным, или малым и положительным, или малым и отрицательным). Случайные члены должны быть абсолютно не зависимы друг от друга.

В силу того, что , данное условие можно записать следующим образом:

(3.14)

Если это условие не будет выполнено, то регрессия, оцененная по обычному методу наименьших квадратов, вновь даст неэффективные результаты. В главе 7 рассматриваются возникающие здесь проблемы и пути их преодоления.

4-е условие Гаусса - Маркова: случайный член должен быть распределен независимо от объясняющей переменной.

Часто, в сущности, используется более сильное предположение о том, что объясняющая переменная не является стохастической, т. е. не имеет случайной составляющей. Значение любой независимой пе­ременной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.

Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю. Так как , то:

(3.15)

Следовательно, данное условие можно записать также в виде:

(3.16)

Наряду с условиями Гаусса - Маркова обычно также предполагается нормальность распределения случайного члена. Дело в том, что если Случайный член и нормально распределен, то также будут распределены, и коэффициенты регрессии. Это условие пригодится нам позже, когда потребуется проводить проверку гипотез и определять доверительные интервалы для , используя результаты построения регрессии.

Предположение о нормальности основывается на центральной предельной теореме. В сущности, теорема утверждает, что если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не является доминирующей, то она будет иметь приблизительно нормальное распределение, даже если отдельные составляющие не имеют нормального распределения.

Случайный член u определяется несколькими факторами, которые не входят в явной форме в уравнение регрессии. Поэтому даже если мы ничего не знаем о распределении этих факторов (или даже об их сущности), мы имеем право предположить, что они нормально распределены.

Дадим следующую формулировку теоремы Гаусса - Маркова: если выполнены условия Гаусса - Маркова для модели парной регрессии, то МН/С дает несмещенные, эффективные и состоятельные оценки параметров регрессии а и b.

Если предположения 2) и 3) нарушены, то есть дисперсия возмущений непостоянна и/или значения связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности - нет.

При невыполнении предположения может нарушаться и свойство несмещенности оценок, являющееся наиболее важным в эконометрическом анализе. Значительная часть современной эконометрической теории посвящена анализу выполнения данного свойства (в совокупности с остальными) в различных конкретных ситуациях, а также выяснению и корректировке последствий его невыполнения.

В 1 главе мы рассматривали оценки неизвестного математического ожидания и случайной величины х по данным выборочных наблюдений, Хотя мы интуитивно использовали в качестве оценки для х выборочное среднее х, было показано, что оно является лишь одной из бесконечного числа возможных несмещенных оценок этого параметра. Причина предпочтения выборочного среднего всем другим оценкам состоит в том, что при определенных предположениях оно является наиболее эффективным.

Аналогичные рассуждения применимы и к коэффициентам регрессии. Мы увидим, что оценки по обычному методу наименьших квадратов являются не только несмещенными оценками коэффициентов регрессии, но и наиболее эффективными в том случае, если выполнены условия Гаусса - Маркова. С другой стороны, если условия Гаусса-Маркова не выполнены, то, вообще говоря, можно найти оценки, которые будут более эффективными по сравнению с оценками, полученными обычным методом наименьших квадратов. Рассмотрим иллюстрацию. Предположим, что мы имеем зависимость, заданную уравнением (3.1), и сосредоточим внимание на оценках для Человек, не знакомый с регрессионным анализом, увидев диаграмму разброса для выборки наблюдений, может попытаться получить оценку тангенса угла наклона путем простого объединения первого и последнего наблюдений и деления прироста высоты на горизонтальный отрезок между ними, как показано на рис. 3.3. Оценка b в этом случае будет определяться следующим образом:

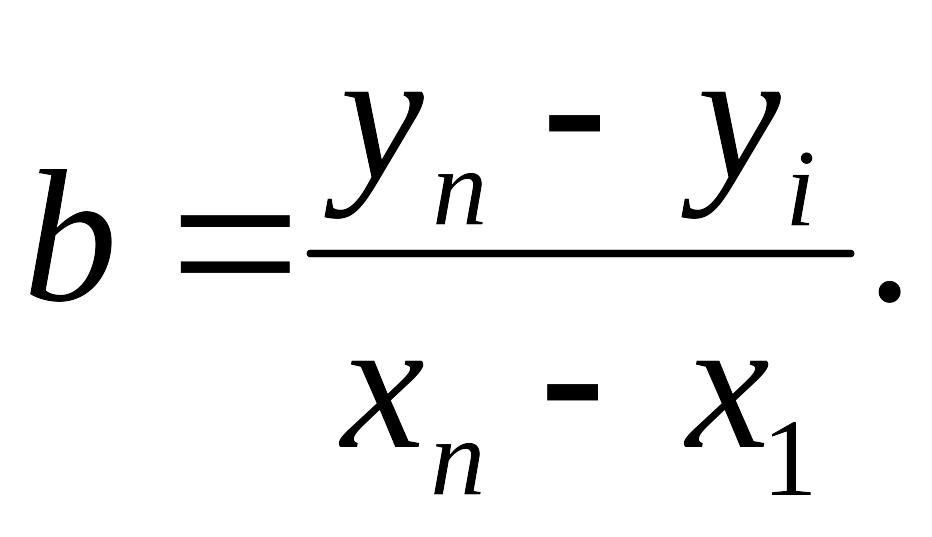(3.17)

Каковы свойства этой оценки? Сначала мы исследуем, является ли она несмещенной. Используя уравнение (3.1) применительно к первому и последнему наблюдениям, получим:

(3.18)

(3.19)

Следовательно,

(3.20)

Таким образом, мы разложили "наивную" оценку на две составляющие: истинное значение и остаточный член. Это разложение выполнено подобно тому, как это сделано в разделе 3.1 для оценки МНК. Однако остаточный член является другим. Предполагая M(u)=0, мы имеем, что математические ожидания, как так и , равны нулю, но тогда математическое ожидание остаточного члена в уравнении (3.20) также равно нулю. Таким образом, несмотря на то что эта оценка столь "наивна", она является несмещенной.

Это, разумеется, не единственная оценка, которая наряду с оценкой, полученной методом МНК, обладает свойством несмещенности. Вы можете получить еще одну оценку такого типа путем объединения двух произвольно выбранных наблюдений, а если вы хотите рассмотреть менее "наивные" процедуры, то здесь открываются поистине безграничные возможности.

Интуитивно легко понять, что мы не предпочтем "наивную" оценку типа (3.17) оценке МНК. В отличие от оценки МНК, в которой учитывается каждое наблюдение, в "наивной" оценке берется только первое и последнее наблюдения и не используется большая часть имеющейся в выборке информации. "Наивная" оценка зависит от значений остаточного члена и в данных двух наблюдениях, тогда как оценка по методу наименьших квадратов объединяет все значения остаточного члена и более эффективно использует возможность того, что эти значения в некоторой степени взаимно "погашаются".

При сравнении с менее "наивными" оценками превосходство оценки МНК в эффективности может быть не столь очевидным. Тем не менее в том случае, если условия Гаусса - Маркова для остаточного члена выполнены, коэффициенты регрессии, построенной обычным методом наименьших квадратов, будут наилучшими линейными несмещенными оценками, (best linear unbiased estimators, или BLUE): несмещенными, как мы покажем ниже, так как они являются линейными функциями значений у; наилучшими, так как они являются наиболее эффективными в классе всех несмещенных линейных оценок. Теорема Гаусса - Маркова как раз и доказывает это.