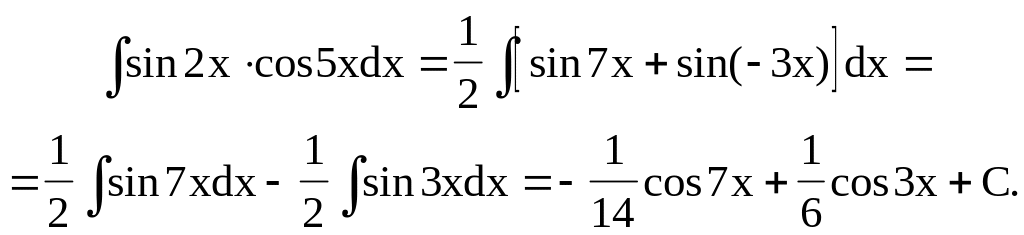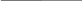1.6.9.1. Интегралы вида , где r - рациональная функция
9.1.
Такие интегралы приводятся к интегралам
от рациональных функций с помощью
универсальной
тригонометрической подстановки
В результате этой подстановки имеем
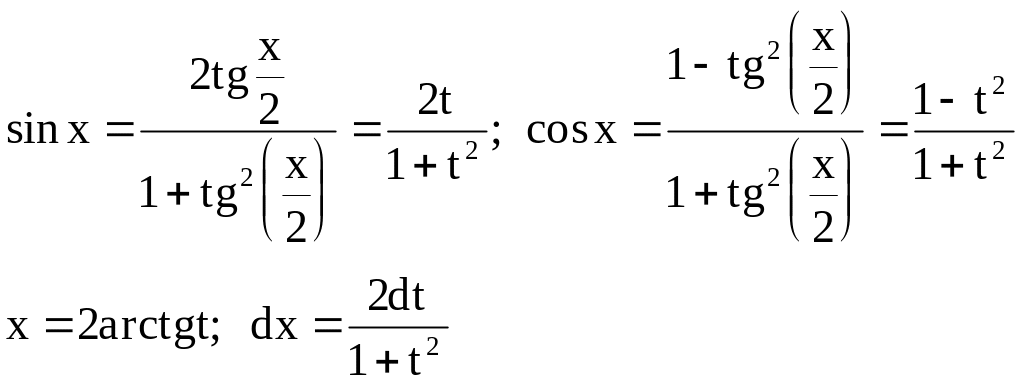
Пример.
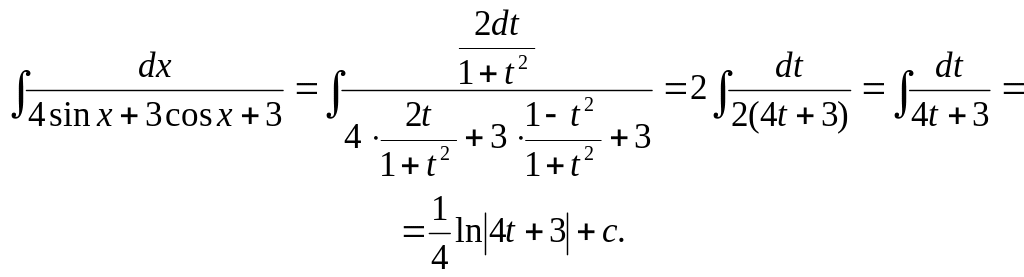
Возвращаясь к старой переменной, получим
Замечание.
Универсальная подстановка
во многих случаях приводит к сложным
вычислениям, так как при ее применении
sinx и cosx выражаются через t в виде
рациональных дробей t2
.
В некоторых частных случаях нахождение интегралов вида может быть упрощено.
1. Если
- нечетная функция относительно sinx, т.е.
,
то интеграл рационализируется подстановкой
cosx=t.
2.
Если
- нечетная функция относительно cosx, т.е.
,
то интеграл рационализируется с помощью
подстановки sinx=t.
3. Если
- четная функция относительно sinx и cosx,
т.е. если
,то
следует применить подстановку tgx=t.
Примеры.
1.
Так как подынтегральная
функция нечетна относительно sinx, то
полагаем cosx=t. Отсюда
.
Таким образом,
.
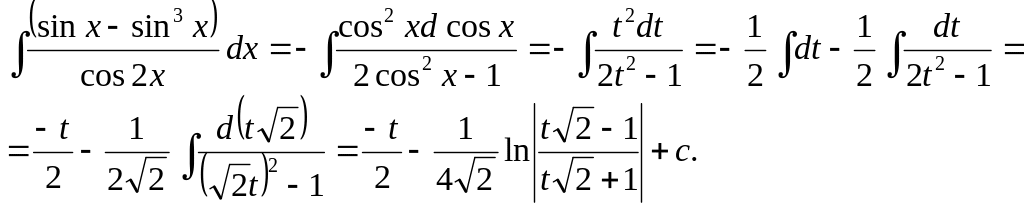Следовательно,
.
2.
Здесь подынтегральная
функция является нечетной относительно
косинуса. Поэтому применяем подстановку
sinx=t, тогда
.
Следовательно,
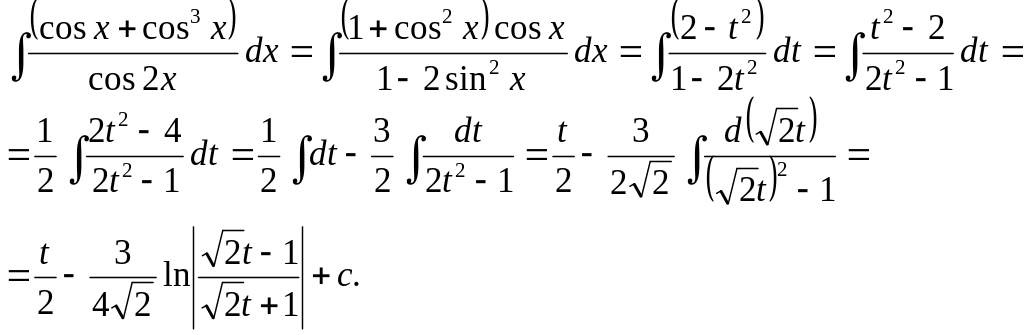
Окончательно получим:
Заметим, что в этом случае интеграл всегда может быть записан в виде
.
3.
Здесь подынтегральная функция является четной относительно sinx и cosx, поэтому полагаем t=tgx.
Тогда
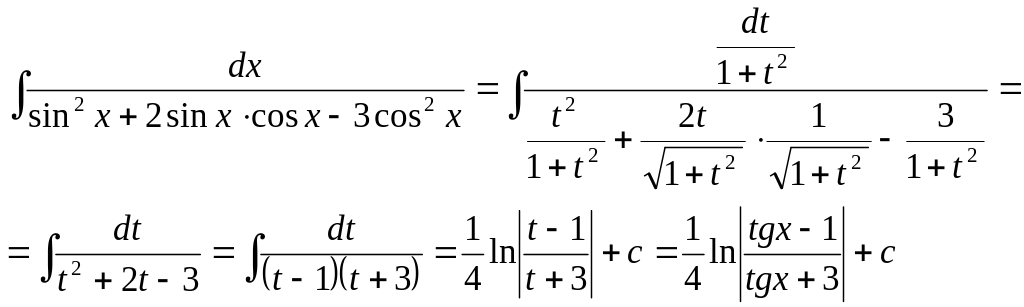
Замечание. То же преобразование можно сделать проще, если в исходном интеграле числитель и знаменатель разделить на cos2x.
.
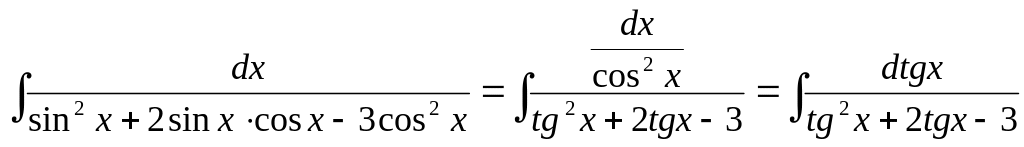1.6.9.2. Интегралы вида
1-й случай. По крайней мере один из показателей m или n нечетное целое, положительное число.
Если n нечетно, то применяется подстановка sinx=t, если же m нечетно, то подстановка cosx=t.
Примеры.
1.
Положим sinx=t, cosxdx=dt, тогда
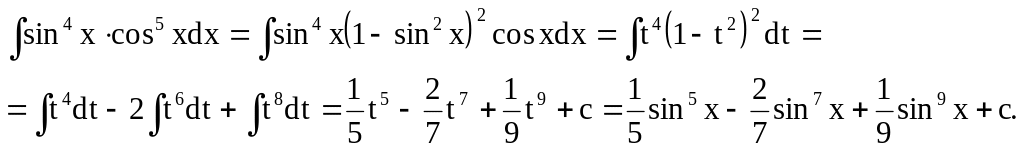
2.
Положив cosx=t, -sinxdx=dt, получим:
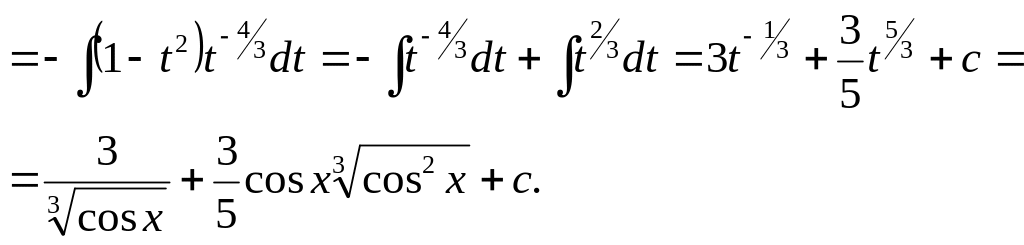
2-ой случай. Показатели степеней m и n - четные положительные числа. Здесь нужно преобразовать подынтегральную функцию с помощью формул.
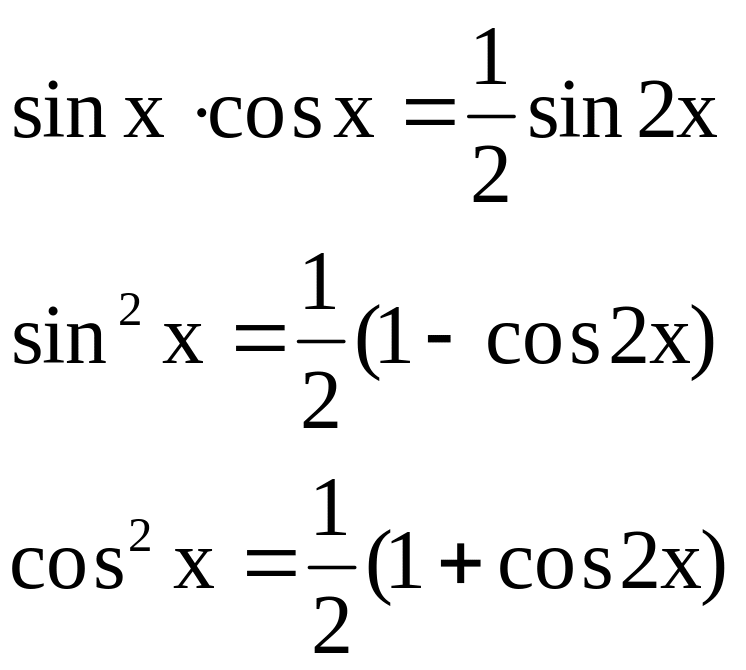
Пример. 
.
Здесь
Отсюда
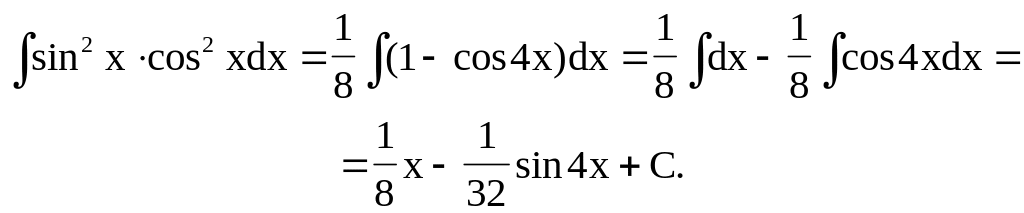
1.6.9.3. Интегралы вида ,
где m - целое положительное число
При нахождении таких интегралов применяется формула
,
с помощью которой последовательно снижается степень тангенса и котангенса.
Пример.
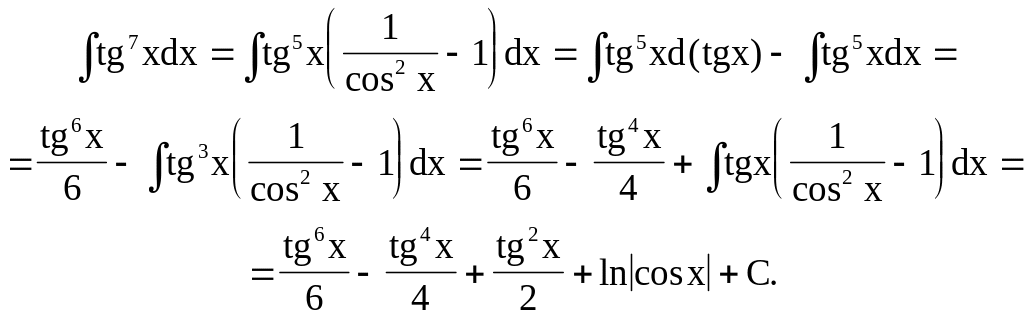
1.6.9.4. Интегралы вида
Используя формулы
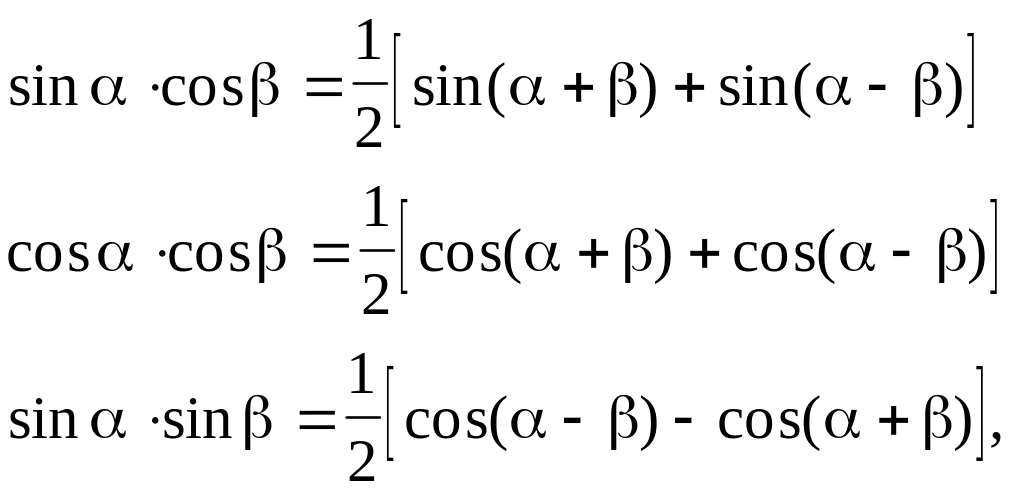
представляем подынтегральную функцию в виде суммы косинусов или синусов.
Пример.
