1.6.8.2. Интегрирование некоторых иррациональностей

1.6.8.2.1. Рациональные функции от нескольких аргументов

Определение 1. Многочленом степени n от двух аргументов x и y называется выражение вида

,

в котором через обозначены постоянные вещественные числа такие, что среди чисел есть хотя бы одно число, отличное от нуля.

Определение 2. Рациональной функцией от двух аргументов x и y называется выражение вида

,

где P_n(x,y) и Q_m(x,y) - многочлены от двух переменных степени n и m соответственно.

Утверждение. Если R(x,y) - рациональная функция от двух аргументов x и y, R₁(t), R₂(t), R₃(t) - три произвольных рациональных функции от одной переменной t, то выражение

представляет собой рациональную функцию от одной переменной.

Замечание. В дальнейшем для доказательства интегрируемости в элементарных функциях некоторых выражений мы будем посредством специально подобранной подстановки сводить интеграл от рассматриваемых выражений к интегралу от рациональной дроби.

1.6.8.2.2. Интегрирование выражений вида

,

где mN⁺, , , ,  = const.

Положим , тогда .

Интеграл перейдет в .

Пример. .

Здесь дробно-линейная функция , в частности, свелась просто к линейной функции x+1. Полагаем , тогда

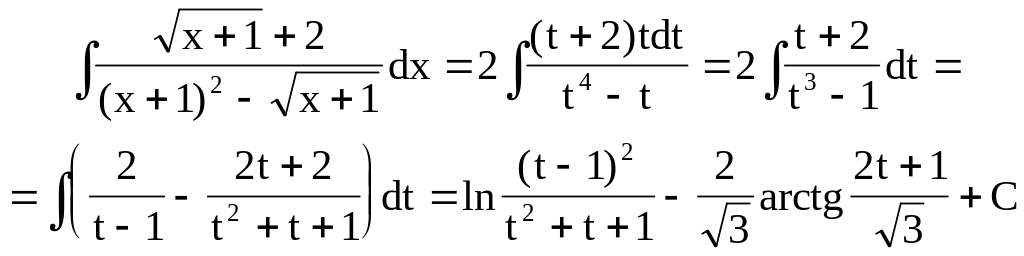
где остается лишь подставить .

а) Этот интеграл легко сводится к табличному, если выделить в трехчлене ах²+bх+c полный квадрат.

Пример

x²+2x+5 = (x+1)²+4

Отсюда,

б) . В числителе дроби необходимо выделить производную квадратного трехчлена.

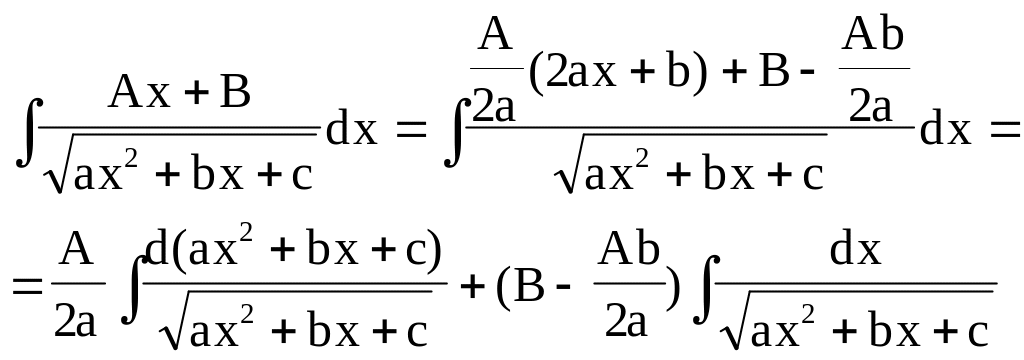
Пример

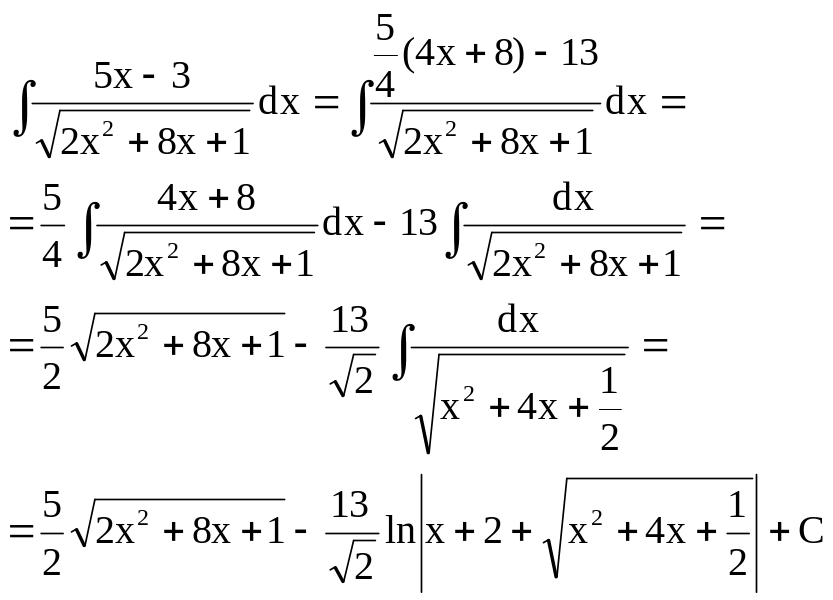
1.6.8.2.3. Тригонометрические и гиперболические подстановки

В интегралах вида можно выделить полный квадрат в трехчлене ах²+bx+c и свести их линейной заменой к интегралам вида

.

Для вычисления этих интегралов часто оказывается удобным использовать тригонометрические подстановки

t=sinu, t=cosu, t=tgu,

а также гиперболические подстановки

t=shu, t=chu, t=thu.

Пример .

Положим, x=sint, тогда dx=costdt и заданный интеграл принимает вид

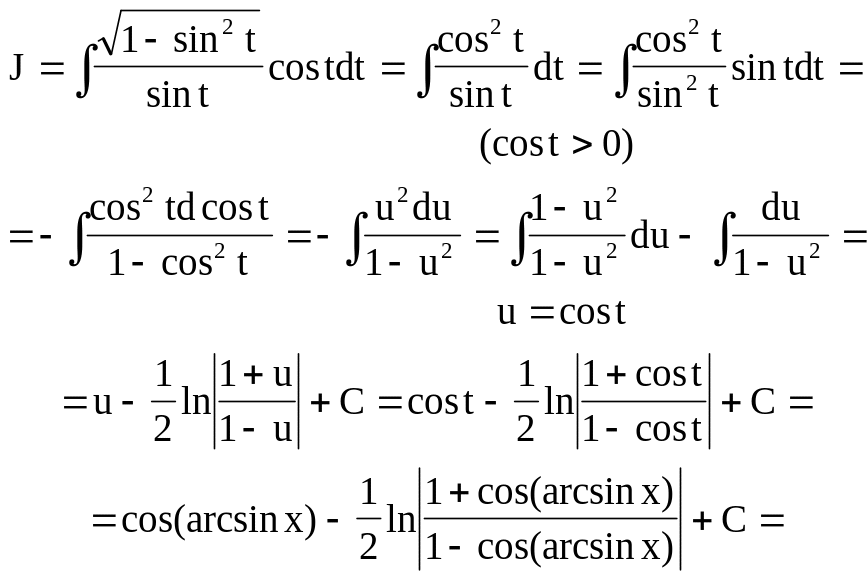
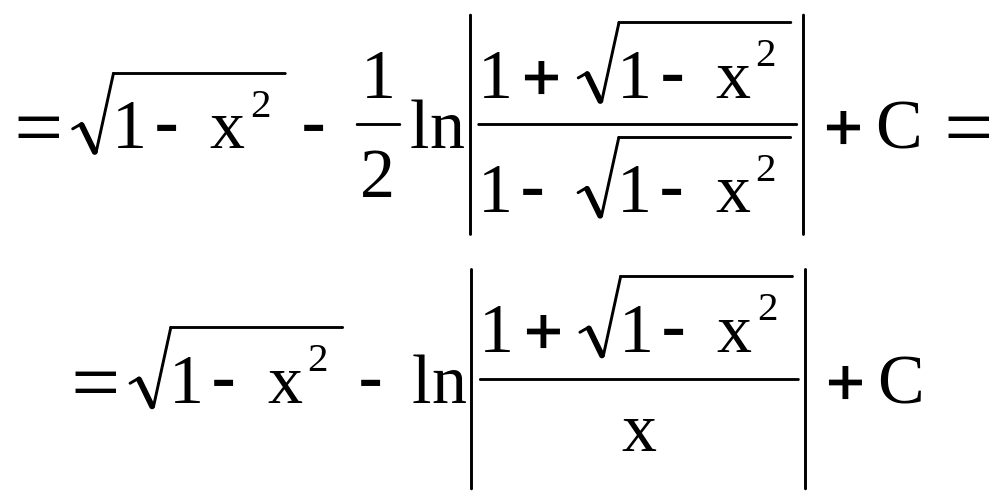
1.6.8.2.4. Интегрирование биноминальных дифференциалов

где а, b - любые постоянные; m, n и p - рациональные числа. Рационализирующая подстановка существует в трех случаях.

1. p - целое

, где r - наименьшее общее кратное знаменателей рациональных чисел m и n.

Подстановка

2. - целое.

Положим z=xⁿ, обозначив , будем иметь

(q - целое).

Это есть интеграл вида , где s - знаменатель числа р. Рационализирующая подстановка имеет вид , или для исходного интеграла .

3. - целое. Сначала положим z=xⁿ

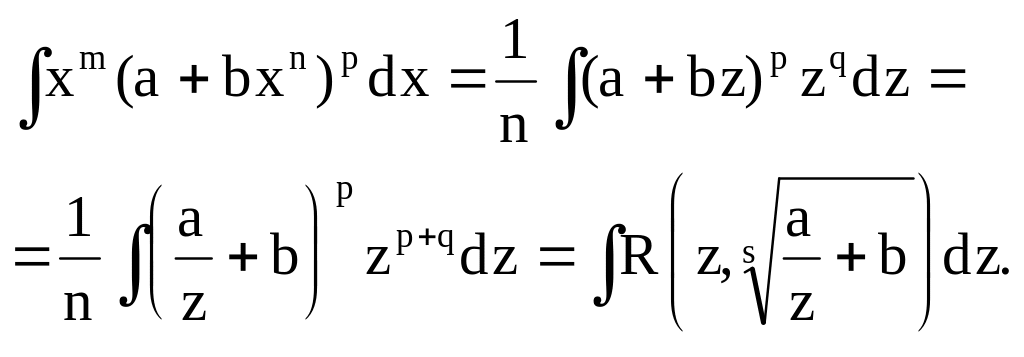
Здесь p+q=p+ - целое, поэтому рационализирующая подстановка , или для исходного интеграла , где s - знаменатель числа р.

Примеры.

1.

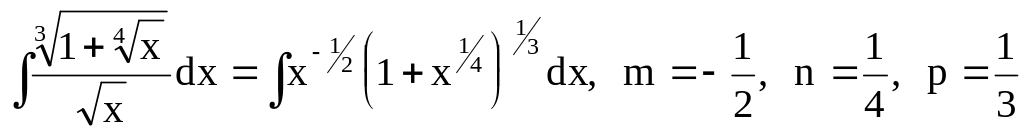
Так как 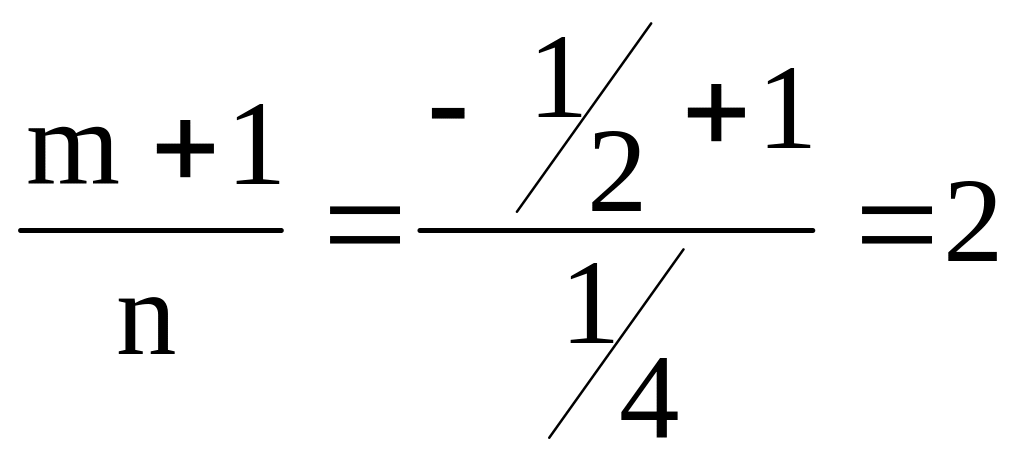, то имеем второй случай (знаменатель р

равен 3).

Положим , тогда

2.

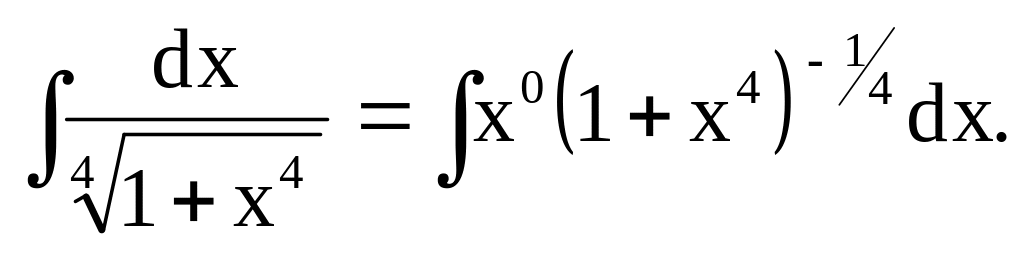
Здесь m=0, n=4, ; третий случай интегрируемости, так как

целое; ; знаменатель р равен 4.

Положим

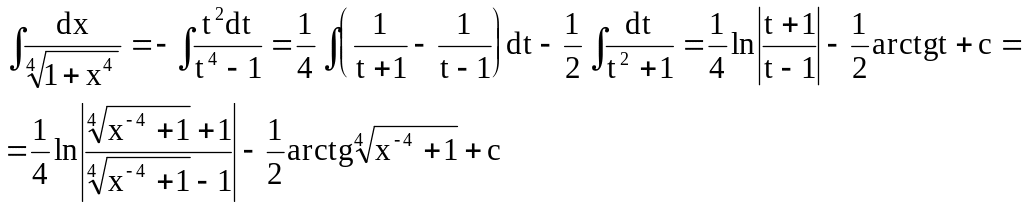
1.6.9. Интегрирование тригонометрических функций