1.2.1.2. Исследование формы эллипса

Приступим к изучению формы эллипса. В уравнении эллипса содержатся только члены с четными степенями текущих координат. Отсюда следует важная геометрическая особенность: эллипс, определяемый уравнением

,

симметричен как относительно оси Ox, так и относительно оси Oy. Другими словами, если точка М₀(x₀;y₀) лежит на эллипсе, то точки М₁(x₀;-y₀), M₃(-x₀;y₀), M₄(-x₀;-y₀), симметричные точке М₀ соответственно относительно оси Ox, оси Oy и начала О, также лежат на эллипсе. Это позволяет изучение формы и построения эллипса ограничиться первым квадрантом, а затем получившуюся кривую с помощью зеркального отражения построить во всех четырех квадрантах. В случае канонического задания эллипса координатные оси являются осями симметрии эллипса. Точка пересечения осей симметрии называется центром эллипса.

Из канонического уравнения эллипса выразим y через х:

.

Так как изучение формы эллипса достаточно провести в первом квадранте, то в этом равенстве надо взять лишь знак плюс, то есть

и полагать, что х  0.

Рис.2

При х=0 имеем y=b. Следовательно, точка B1(0;b) лежит на эллипсе. При возрастании х от 0 до а y убывает. При х=а имеем y=0. Следовательно, точка А1(а;0) лежит на эллипсе. При x>a получаем мнимые значения y. Следовательно, точек эллипса, у которых х>a, не существует.

Дадим переменной х несколько значений, 0<x<a, и, получив соответствующие значения y, b>y>0, построим ряд точек, принадлежащих эллипсу. Учитывая высказанные ранее соображения и соединив найденные точки эллипса плавной линией, получим дугу эллипса В₁А₁ в первом квадранте. Произведя зеркальное отображение дуги В₁А₁ относительно координатных осей, получим весь эллипс. Отсюда следует, что эллипс представляет собой замкнутую кривую, с двумя взаимно перпендикулярными осями симметрии.

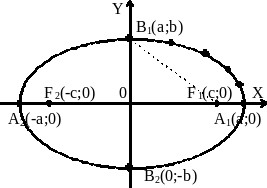
Отрезок А₂А₁ и его длина 2а называется большой осью эллипса, отрезок ОА₁ и его длина а называется большой полуосью эллипса. Отрезок В₂В₁ и его длина 2b называются малой осью эллипса; отрезок ОВ₁ и его длина b называется малой полуосью эллипса. Длина отрезка F₂F₁, то есть число 2с, называется фокусным расстоянием. Точки пересечения эллипса с его осями А₁, А₂, В₁, В₂ называются вершинами эллипса, а точка пересечения его осей называется центром эллипса.

Примечание. Если a=b, то уравнение эллипса имеет вид или x²+y²=a². Это уравнение окружности с центром в начале координат и радиусом, равным а. Можно сказать, что окружность является частным случаем эллипса.

1.2.1.3. Эксцентриситет и фокальные радиусы эллипса

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси эллипса; обозначив эксцентриситет буквой , получим:

 = .

Так как с<a, то <1, то есть эксцентриситет каждого эллипса меньше единицы.

Учитывая, что с² = а² - b²; поэтому

 ;

отсюда

 .

Cледовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем больше эксцентриситет к единице, тем меньше 1 - ², тем меньше, следовательно, отношение ; значит, чем больше эксцентриситет, тем более эллипс вытянут. Наоборот, чем больше отношение , тем меньше эксцентриситет и эллипс является менее вытянутым. В предельном случае, когда b = a, то есть когда эллипс обращается в окружность, его эксцентриситет обращается в нуль.

Пусть M(x;y) - произвольная точка, лежащая на данном эллипсе. Если r₁ и r₂ - фокальные радиусы этой точки, то

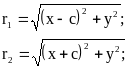
из равенства (6) п. 1 следует:

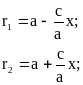
или, так как  , то:

r₁ = a - x;

r₂ = a + x.

В заключение отметим: из определения эллипса непосредственно вытекает способ построения его при помощи нити: если концы нерастяжимой нити длины 2а закрепить в фокусах F₁ и F₂ и натянуть нить острием карандаша, то при движении острия оно будет вычерчивать эллипс с фокусами F₁ и F₂ и суммой фокальных радиусов 2а.