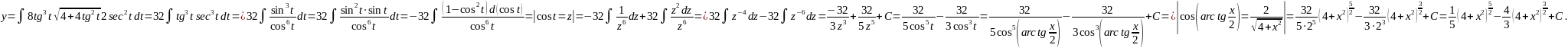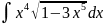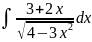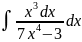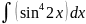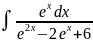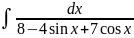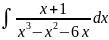- •1 Методические указания
- •1.1 Понятия неопределённого интеграла. Свойства
- •1.2 Непосредственное интегрирование
- •1.3 Метод подстановки
- •1.4 Вычисление интегралов типа
- •1.5 Вычисление интегралов типа
- •1.6 Метод интегрирования по частям
- •1.7 Интегрирование рациональных функций
- •1.8 Интегрирование некоторых классов иррациональных функций
- •1.9 Интегрирование тригонометрических функций
- •1.10 Тригонометрические подстановки
- •2 Нулевой вариант
- •3 Решение 0 варианта
- •4 Расчетные задания
2 Нулевой вариант
Вычислить интегралы.
1.
|
8.
|
2.
|
9.
|
3.
|
10.
|
4.
|
11.
|
5.
|
12.
|
6.
|
13.
|
7.
|
14.
|
|
15.
|
3 Решение 0 варианта
Пример 1
Вычислить
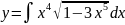
Решение.
Так как
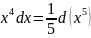 ,
то, используя свойства дифференциала
,
то, используя свойства дифференциала
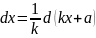 получаем
получаем
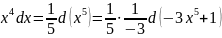 ,
обозначив
,
обозначив
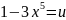 получаем
получаем
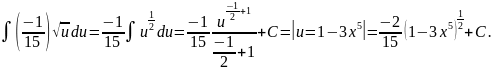
Пример 2
Вычислить
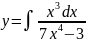
Решение.
Внесём
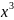 под знак дифференциала
под знак дифференциала
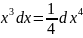 и используя формулу
и используя формулу
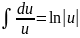 получим:
получим:
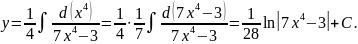
Пример 3
Вычислить
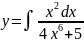
Решение.
Внесём
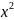 под знак дифференциала и воспользуемся
формулой
под знак дифференциала и воспользуемся
формулой
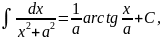 тогда, так как
тогда, так как
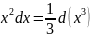 и
и
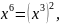 получаем
получаем
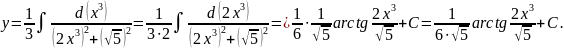
Пример 4
Вычислить
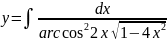
Решение.
Сделаем подстановку
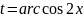 ,
продифференцируем данное равенство
,
продифференцируем данное равенство
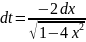 ,
поэтому
,
поэтому
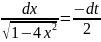 ,
,
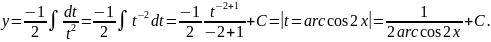
Пример 5
Вычислить
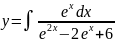
Решение:
Поскольку
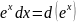 ,
сделаем замену
,
сделаем замену
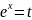 ,
тогда
,
тогда
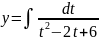 .
При вычислении интегралов содержащих
квадратный трёхчлен в знаменателе
выделим в знаменателе полный квадрат
по переменной
.
При вычислении интегралов содержащих
квадратный трёхчлен в знаменателе
выделим в знаменателе полный квадрат
по переменной
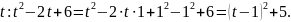 Получаем
Получаем
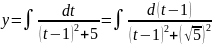 =
=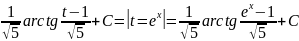
Пример 6
Вычислить
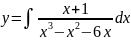
Решение: Это интеграл от правильной алгебраической дроби, т.к. степень многочлена в числителе меньше степени многочлена в знаменателе. Разложим знаменатель на множители
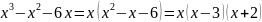
т.к. корни действительные и различные, то данная правильная дробь может быть представлена в виде суммы простейших дробей вида:
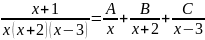
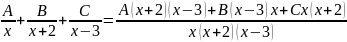
Для
нахождения чисел
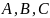 воспользуемся методом частных значений.
воспользуемся методом частных значений.
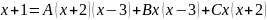
полагаем:
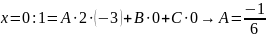
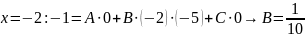
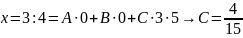
следовательно
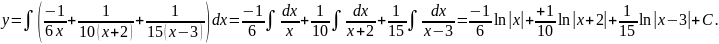
Пример 7
Вычислить
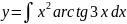
Решение:
Т.к. под интегралом стоит произведение
многочлена на обратную тригонометрическую
функцию, то используем метод интегрирования
по частям
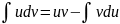 .
.
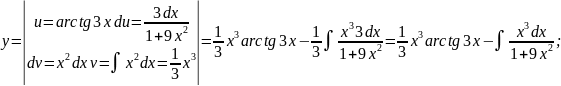
Интеграл
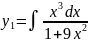 ,
под знаком интеграла стоит неправильная
алгебраическая дробь, выделим целую
часть, выполнив деление многочлена на
многочлен уголком, получаем
,
под знаком интеграла стоит неправильная
алгебраическая дробь, выделим целую
часть, выполнив деление многочлена на
многочлен уголком, получаем
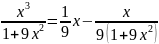
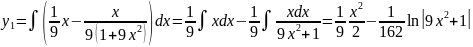
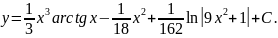
Пример 8
Вычислить
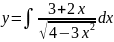
Решение:
Представим интеграл в виде суммы двух
интегралов
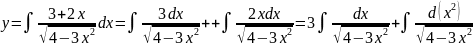 .
.
Внеся
множители под знак дифференциала и
используя табличные интегралы
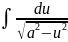 ;
;
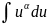 получаем
получаем
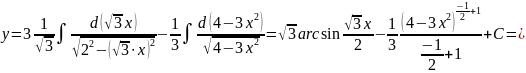
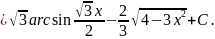
Пример 9
Вычислить
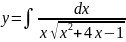
Решение:
. Подстановка
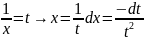 сводит данный интеграл к виду
сводит данный интеграл к виду
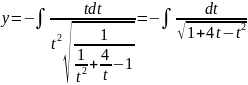 ,
который сводится к табличному выделением
в знаменателе полного квадрата по
переменной
,
который сводится к табличному выделением
в знаменателе полного квадрата по
переменной
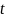 .
.
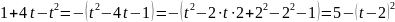 ,
получаем
,
получаем
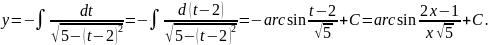
Пример 10
Вычислить
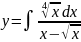
Решение:
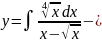 интеграл от дробных степеней переменной
,
наименьшее общее кратное знаменателей
интеграл от дробных степеней переменной
,
наименьшее общее кратное знаменателей
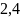 равно
равно
 ,
поэтому полагая
,
поэтому полагая
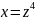 ,
,
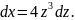 Подставив получаем:
Подставив получаем:
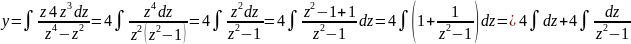 =
=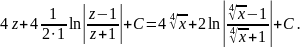
Пример 11
Вычислить
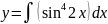
Решение:
Под знаком интеграла стоит чётная
степень синуса, используем формулу
понижения степени
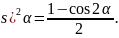
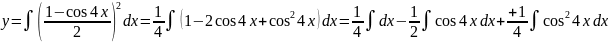 =
=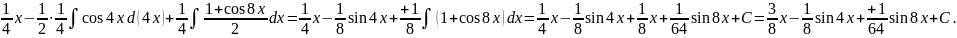
Пример 12
Вычислить
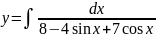
Решение:
Под интегралом стоит рациональная
функция относительно
.
Применим универсальную тригонометрическую
подстановку
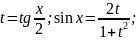
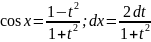 ,
,
получаем
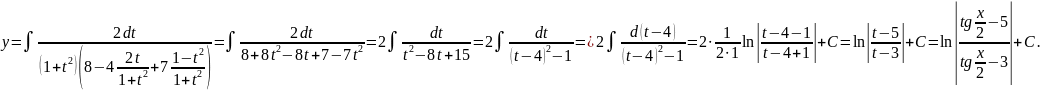
Пример 13
Вычислить
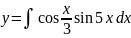
Решение:
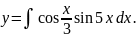
Под
знаком интеграла стоит произведение
тригонометрических функций, используя
формулы преобразования произведения
в сумму, получаем
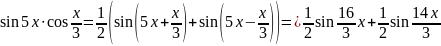 .
Подставляем
.
Подставляем
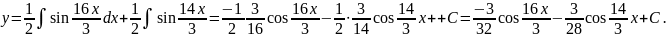
Пример 14
Вычислить
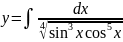
Решение:
Подинтегральную функцию можно представить
в виде произведения
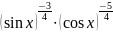 .
Сумма показателей
.
Сумма показателей
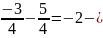 чётное число, поэтому числитель и
знаменатель разделим на
чётное число, поэтому числитель и
знаменатель разделим на
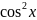 .
.
=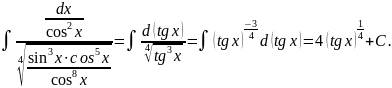
Пример 15
Вычислить
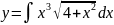
Решение
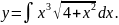 Воспользуемся подстановкой
Воспользуемся подстановкой
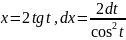 ,
которая приводит интеграл к рациональному
виду.
,
которая приводит интеграл к рациональному
виду.