Тема 2. Элементы аналитической геометрии

1. Угловой коэффициент прямой - это тангенс угла наклона прямой к оси OX.

Будем обозначать его буквой k. Следовательно, k = tg

2. Уравнение прямой с угловым коэффициентом

Если прямая не параллельна оси OY , то ее уравнение y = kx + b, где b - ордината точки пересечения прямой с осью OY, k - угловой коэффициент прямой, (x,у) - координаты любой точки на прямой.

3. Уравнение прямой, проходящей через точку M₀ (x₀ ,y₀ ) и имеющей угловой коэффициент k, y - y₀ = k (x - x₀ ),

где (x₀ ,y₀ ) - координаты заданной точки на прямой, k - угловой коэффициент прямой, (x,y) - координаты любой точки на прямой.

4. Уравнение прямой, проходящей через две заданные точки M₁(x₁ ,y₁) и M₂ (x₂ ,y₂),

где (x ₁,y ₁) - координаты одной точки на прямой, (x₂ ,y₂ ) - координаты другой точки на прямой, (x,y) - координаты любой точки на прямой.

5. Общее уравнение прямой: Ax + By + C = 0,

где A, B, C - заданные числа, причем A и B одновременно в нуль не обращаются, (x,y) - координаты любой точки на прямой. Если B не обращается в нуль, то уравнение можно преобразовать следующим образом : , тогда

6. Условие параллельности двух прямых: k₁ = k₂,

где k₁ и k₂ - угловые коэффициенты прямых.

7. Условие перпендикулярности двух прямых

k ₁ k₂ = -1 ,

где k ₁ и k ₂ - угловые коэффициенты прямых.

8. Нахождение координат середины отрезка

Если точка A имеет координаты (x_a,y_a), а точка B - (x_b,y_b), то координаты середины О отрезка АB можно найти по формулам:

9. Нахождение длины отрезка

Если точка А имеет координаты (x_a ,y_a), а точка В - (x _b,y_b ), то длину отрезка АВ можно найти по формуле :

10. Деление отрезка в данном отношении

Если точка A имеет координаты (x_a ,y_a ), а точка B - (x_b ,y_b ), то координаты точки С делящей отрезок АB в отношении m : n можно найти по формулам :

Тема 3. Предел функции

Определение Областью определения функции называют те значения , для которых данное выражение имеет смысл и значения конечны.

Определение Пусть функция определена в некоторой окрестности точки . Если для любого > 0 найдется такое число > 0, что при всех , удовлетворяющих неравенству , будет выполнено неравенство

, то число называют пределом функции в точке , то есть A= .

Для существования предела функции в точке необходимо и достаточно, чтобы существовали и были равны левосторонний и правосторонний пределы в этой точке.

Определение Если для любого существует > 0, такое, что при всех из - окрестности будет выполнено условие , то предел функции в точке равен бесконечности: .

Определение Если же для любого существует , такое, что при всех , то является пределом функции при , стремящемся к бесконечности: .

Отметим следующие свойства пределов:

1. Если существует, то он единственный;

2.  ( постоянное число);

3. 

4. 

5.  ( )

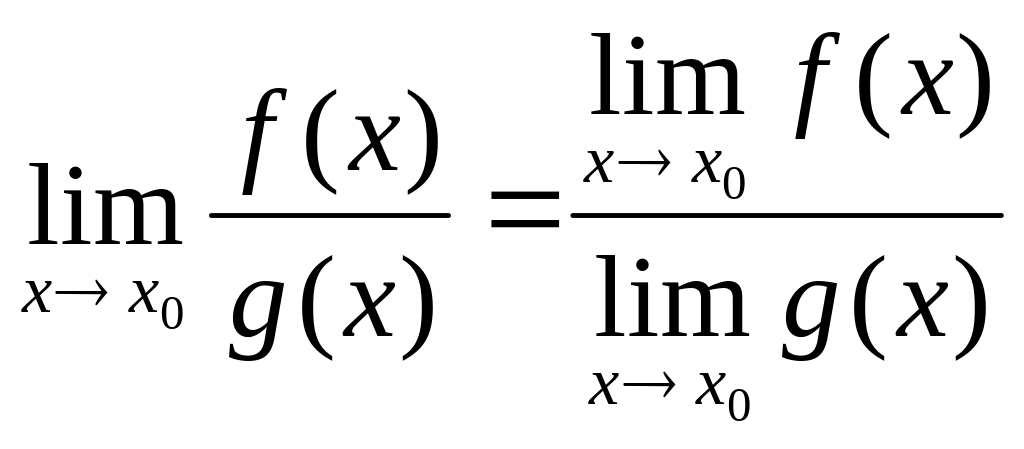Для вычисления пределов важны следующие свойства бесконечно малых величин. Пусть и ─ бесконечно малые, а ─ ограниченная функция в окрестности точки . Тогда верны утверждения:

1.  ─ бесконечно малая величина в окрестности точки ;

2.  ─ бесконечно малая величина в окрестности точки ;

3.  ─ бесконечно малая величина в окрестности точки ;

4. Если существует , то это равносильно тому, что в окрестности точки , где ─ бесконечно малая величина в окрестности этой точки.