
- •Понятие ду 1-го порядка, его решения, общего решения, частного решения.
- •Ду с разделяющимися переменными и его решения.
- •19Стр в лекции
- •3. Задача Коши для ду 1-го порядка.
- •4. Однородное ду 1-го порядка и его решение.
- •6. Ду Бернулли и его решение.
- •7. Ду высших порядков. Основные определения Теорема Коши.
- •8. Ду, допускающее понижение порядка.
- •9. Линейное ду высших порядков.
- •10. Фундаментальная система лоду. Определитель Вронского.
- •11. Теорема о структуре общего решения лоду.
- •12. Линейные ду с постоянными коэффициентами.
- •13. Структура общего решения лоду.
- •14. Алгоритм построения общего лоду 2-го порядка с постоянными коэффициентами.
- •15. Структура общего решения лоду 2-го порядка.
- •16. Подбор частного решения лнду 2-го порядка с постоянными коэффициентами.
- •17. Метод вариации производных постоянных 2-го порядка с постоянными коэффициентами.
- •18. Нормальная система ду и понятие её решения.
- •19. Общее решение системы ду.
- •20. См вопрос 19.
- •21, 22. Понятие двойного интеграла. Свойства двойного интеграла
- •23. Вычисление двойного интеграла.
- •24. Понятие тройного интеграла и его свойства.
- •25. Криволинейные интегралы 1-го рода.
- •26.Свойства криволинейных интегралов 1-го рода
- •27. Криволинейный интеграл второго рода.Его свойства.
- •28.Ротор векторного поля
- •29.Дивергенция векторного поля.
- •Решение
- •30.Формула Стокса.
- •31.Понятие потенциального поля.
- •32. Понятие числового ряда и его сходимости
- •33. Необходимый признак сходимости числового ряда.
- •35.Признак Даламбера
- •36.Радикальный признак Коши.
- •37.Признак Лейбница Сходимости знакочередующегося ряда.
35.Признак Даламбера
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
![]()
существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство
![]()
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
![]()
то ряд расходится.
36.Радикальный признак Коши.
Если
для ряда ![]() с
неотрицательными членами существует
такое число q<1,
что для всех достаточно больших n выполняется
неравенство
с
неотрицательными членами существует
такое число q<1,
что для всех достаточно больших n выполняется
неравенство
![]() ,
,
то ряд сходится, если же для всех достаточно больших n выполняется неравенство
![]()
то ряд расходится.
Следствие. Если
существует предел ![]() ,
то при <1
ряд сходится, а при >1
ряд расходится.
,
то при <1
ряд сходится, а при >1
ряд расходится.
Пример. Определить
сходимость ряда  .
.

Вывод: ряд сходится.
37.Признак Лейбница Сходимости знакочередующегося ряда.
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Пусть для знакочередующегося ряда
выполняются следующие условия:
Тогда этот ряд сходится. |
Замечания:
Если,
выполнены все условия, и ряд из модулей
(![]() )
сходится, то исходный ряд сходится
абсолютно.
Если выполнены все условия, но ряд из
модулей расходится, то исходный ряд
сходится
условно.
Строгая положительность an существенна.
)
сходится, то исходный ряд сходится
абсолютно.
Если выполнены все условия, но ряд из
модулей расходится, то исходный ряд
сходится
условно.
Строгая положительность an существенна.
Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
![]() .
Ряд из модулей имеет вид
.
Ряд из модулей имеет вид ![]() —
это гармонический
ряд,
который расходится.
—
это гармонический
ряд,
который расходится.
Теперь воспользуемся признаком Лейбница:
знакочередование выполнено

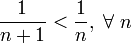
 .
.
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
38.Абсолютная и Условная сходимость рядов.
|
Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки. Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, что
1. an+1 < an для
всех n;
2.
Тогда
знакочередующиеся ряды Абсолютная и условная сходимость Ряд |
||
|
|
Пример 1 |
|
|
|
|
|
Исследовать
на сходимость ряд Решение. Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем
поскольку
39.Определение сходимости в точке функционального ряда. Сходимость
Ряд
называется сходящимся поточечно,
если последовательность Ряд называется сходящимся поточечно, если последовательность его частичных сумм сходится равномерно. Абсолютная и условная сходимость
Ряд Если ряд сходится, а расходится, то ряд называется сходящимся условно. Признаки равномерной сходимости. Ряд сходится абсолютно и равномерно, если выполнены условия:
Частным
случаем является признак
Вейерштрасса,
когда 40.Степенные ряды. Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
в котором коэффициенты an берутся из некоторого кольца R.
42. Радиус и интервал сходимости степенного ряда
Из
теоремы Абеля следует, что если
Т:
Областью сходимости ряда (30.2) является
интервал (-R, R), В каждой точке этого
интервала ряд сходится абсолютно, а
на интервалах
Интервал
(-R, R) называется интервалом сходимости
ряда (30.2), a R — его радиусом сходимости.
Для некоторых рядов интервал сходимости
вырождается в точку (R= 0), для других
— охватывает всю ось OX(R=
Укажем
способ определения радиуса сходимости
ряда (30.2). Рассмотрим ряд из абсолютных
величин его членови применим к нему
признак Даламбера:
Если
При Пример: Найти радиус и интервал сходимости ряда
интервал
абсолютной сходимости ( - 3, 3). На концах
интервала: при х = 3 имеем
при
х= Область сходимости данного ряда — промежуток [-3, 3)
Ряд
(30.1) сводится к ряду (30.2) заменой
переменной
43.Признак Абсолютной сходимости ряда.
Сходящийся ряд
Аналогично,
если несобственный
интеграл
44. Ряды Тейлора и Маклорена. Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
где Rn − остаточный член в форме Лагранжа определяется выражением
Если
приведенное разложение сходится в
некотором интервале x,
т.е.
Если a = 0, то такое разложение называется рядом Маклорена:
45. Разложение некоторых элементарных функций в ряд Маклорена
|
|
||

 и
и 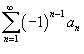 сходятся.
сходятся.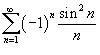 .
.






