6.Векторы, операции над векторами. Скалярное произведение векторов и его свойства.

Алгебраический подход

В линейной алгебре вектор — это элемент векторного пространства (или иначе: линейного пространства). Векторы можно складывать и умножать на число. Вектор также можно представить в виде линейной комбинации других векторов. Базис — это линейно независимая совокупность векторов, которая порождает всё пространство. В конечномерном пространстве существует конечный базис, и тогда любой вектор пространства может быть единственным образом представлен в виде разложения вида

где e1,....en — это базис, а x1,...xn — координаты вектора в заданном базисе.

Геометрический подход

Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (приложенного, закреплённого) вектора.

Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства.

Свободный вектор — класс эквивалентности направленных отрезков.

При этом два направленных отрезка считаются эквивалентными, если они:

-коллинеарны

-равны по длине

-одинаково направлены (сонаправлены)

Многие математические объекты (например матрицы, тензоры, функции и т. д.), в том числе обладающие структурой более общей, чем счётный или конечный упорядоченный список, удовлетворяют аксиомам векторного пространства, то есть являются с точки зрения алгебры векторами.

Вектор, начало которого совпадает с его концом, называют нулевым

Вектор BA называют противоположным вектору AB.

Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка.

Ортогональность

Векторы являются ортогональными тогда и только тогда, когда их скалярное произведение равно нулю.

Часто вместо этого термина употребляют термин "перпендикулярность", однако следует учитывать, что нулевой вектор ортогонален любому вектору, но понятие перпендекулярности для него не определено, поскольку не определён угол между нулевым и другим вектором. Коллинеарность

Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.

Часто вместо этого термина употребляют термин "параллельность", однако следует учитывать, что нулевой вектор коллинеарен любому вектору, но понятие параллельности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Сложение векторов

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.

Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

А модуль (длину) вектора суммы |u+v| = u+v определяют по теореме косинусов

|u+v| = sqrt(|u|2 + |v|2 - 2*|u|*|v|*cos a)

где a — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула

|u+v| = sqrt(|u|2 + |v|2 + 2*|u|*|v|*cos a)

теперь a — угол между векторами выходящими из одной точки.

Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.

Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.

М ы рассмотрели умножение вектора на число. Однако во многих задачах механики и физики встречается операция умножения вектора на вектор. Но при этом результат может быть как числом, так и вектором. Поэтому рассматривают два вида умножения векторов: скалярное и векторное.

Пусть даны два вектора а и б, угол между, которыми равен .

1.Скалярным произведением векторов а и б называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается а*б . Итак, .

Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.

Рассмотрим свойства скалярного произведения.

Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов а и б .

Очевидно, из определения скалярного произведения:

2.Для любого числа λ и любых векторов а,б имеем:

3. Для любых векторов а,б,с выполняется равенство

4. Для любого вектора а, выполняется соотношение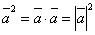

Действительно, так как , то .

Из этого свойства в частности следует

5. Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.

Это свойство очевидно из определения скалярного произведения.

Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.