25.Теорема о связи бесконечно малых и бесконечно больших величин.

Если f (x) — бесконечно большая функция, то есть бесконечно малая функция в этой же точке.

В самом деле, пусть , это означает, что

( K > 0) ( δ = δ(K)> 0) ( 0 < | x - x0 | < δ ) : | f (x) | > K .

Так как |f (x)| > K , то .

Будем считать, что , тогда

( ε > 0) ( δ = δ(ε)> 0) ( 0 < | x - x0 | < δ ) : 1/| f (x)| <ε .

Это означает, что .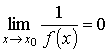

26.Первый замечательный предел.

ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

Функция не определена при x=0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке.

Однако, можно найти предел этой функции при х→0.

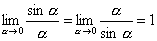
Приведем доказательство записанной формулы. Рассмотрим окружность радиуса 1 и предположим, что угол α, выраженный в радианах, заключен в пределах 0 < α < π/2. (Так как четная функция и ее значения не изменяются при изменении знака α, то достаточно рассмотреть случай, когда α > 0.) Из рисунка видно, что

SΔOAC <Sсект.OAC <SΔOBC.

Так как указанные площади соответственно равны

SΔOAC=0,5∙OC∙OA∙sinα=0,5sinα,Sсект.OAC=0,5∙OC2∙α=0,5α,SΔOBC=0,5∙OC∙BC=0,5tgα.

Следовательно,

sin α < α < tg α.

Разделим все члены неравенства на sin α > 0:

.

Но . Поэтому на основании теоремы 4 о пределах заключаем, что .

Выведенная формула и называется первым замечательным пределом.

Таким образом, первый замечательный предел служит для раскрытия неопределенности . Заметим, что полученную формулу не следует путать с пределами .

27.Второй замечательный предел.

ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом

Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).

28.Непрерывность функции.

Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если

Пусть функция определена в некоторой окрестности точки a, быть может, за исключением самой точки a. Точка a называется точкой разрыва, если эта функция либо не определена в точке a, либо определена, но не является непрерывной в точке a.

Чаще всего разрыв возникает по двум причинам:

1.функция задана различными выражениями на разных участках, и в граничных точках эти выражения имеют различные пределы;

2.функция не определена в данной точке.

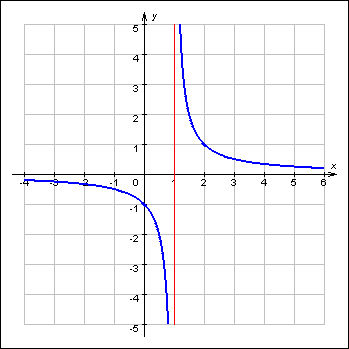
Примером разрывной функции может служить функция зависимости плотности воды в окрестности 0 ºC. Примером непрерывной функции является зависимость площади квадрата от длины его стороны. Подчеркнем еще раз, что непрерывность функции рассматривается только на области ее определения.

Если функция непрерывна в каждой точке некоторого промежутка, то она называется непрерывной на этом промежутке. Большинство функций, изучаемых в элементарной математике, непрерывны на всей области определения. Таковыми являются линейная функция y = kx + b, квадратичная y = ax2 + bx + c, показательная и тригонометрические функции.

Если функции f (x) и g (x) непрерывны в точке x0, то их сумма и произведение также непрерывны в этой точке, а функция непрерывна в ней при условии, что g (x0) ≠ 0.

Отсюда следует, что рациональные функции непрерывны во всех тех точках, в которых их знаменатель не обращается в нуль.

Из непрерывности функции y = f (x) в точке x0 и функции z = g (y) в точке y = f (x0) следует непрерывность сложной функции g (f (x)) в точке x0.

Функцию f (x) называют непрерывной на отрезке [a; b], если она непрерывна в каждой точке интервала (a; b) и, кроме того, непрерывна справа в точке a и слева в точке b.

Теорема Вейерштрасса. Если функция f (x) непрерывна на отрезке [a; b], то она ограничена на этом отрезке и достигает своего наибольшего и наименьшего значения.