Т.Е. Новые координаты точки м(х'у') равны ее старым координатам минус координаты нового начала. Обратно, из (1.1.1) находим

 х = х' + а,

                                  у = у'+ b.                (1.1.2)

Рис.1.2.1

 

Теперь рассмотрим поворот «новой системы» координат О'х'у' относительно «старой системы» Оху на некоторый угол a (рис.1.2.2), т.е.Ðх¢Ох = a считается положительным, если поворот осуществляется против часовой стрелки и отрицательный в противном случае. Определение. Поворотом осей координат называют такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.

Пусть угол b - угол между радиус-вектором точки М (r = OM) и осью Ох¢ ; тогда r, с учетом знака угла b, будет составлять с осью Ох угол

a +b. Тогда на основании формул (1.1) при любом расположении точки М имеем

 

.

А так как новые координаты точки М есть

,                  (1.1.3)

то тогда можно вернуться к старым координатам

.                       (1.1.4)

 

Теперь, если рассмотреть общий случай, когда новое начало координат есть точка О'(а,b) и ось О'х' образует с осью Ох угол a, то на основании формул (1.1.1) и (1.1.4) имеем

 

.            (1.1.5)

           При повороте системы относительно данной на угол -a, необходимо принять во внимание, что cos(-a) = cosa, sin(-a) = -sin(a), будем, соответственно иметь

,    .

3. Введение в математический анализ

1. Числовые множества. Ограниченные и неограниченные множества. Верхние и нижние грани множества. Предельные точки множества.

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

• ‑ множество натуральных чисел;

• ‑ множество целых чисел;

• – множество рациональных или дробных чисел;

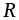• ‑ множество действительных чисел.

Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

Некоторое непустое подмножество множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число такое, что выполняется неравенство ().

Всякое число с указанным свойством называют верхней (нижней) гранью множества .

Непустое подмножество множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество называется неограниченным сверху (снизу), если какое бы число мы бы не предложили в качестве верхней (нижней) границы множества , всегда найдется элемент этого множества, который будет больше (меньше) .

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел называют точной верхней гранью этого множества и обозначают sup . Наибольшую из нижних граней непустого подмножества множества действительных чисел называют точной нижней гранью этого множества и обозначают inf . Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Граничной точкой множества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.

Граница множества – совокупность граничных точек множества:

• (множество натуральных чисел) ограниченно снизу (например, числом ) и не ограничено сверху;

• (множество действительных чисел) неограничено;

• множество отрицательных чисел неограничено снизу и ограничено сверху.

Определение

Окрестностью точки a называется любой интервал, содержащий точку a. .

Проколотой окрестностью точки a называется окрестность точки a, не включающая саму точку a. .

 

Определение

a - предельная точка множества A, если в любой проколотой окрестности точки a есть точки из множества A: .

1. Отрезок. Любая точка, лежащая вне отрезка, предельной не является. Множество предельных точек отрезка соврадает с самим отрезком.

2. Интервал. Множество предельных точек интервала  совпадает с отрезком .

3. Предельные точки могут как принадлежать A, так и не принадлежать ему.

4. Если точка принадлежит множеству A, то она необязательно является предельной. Точки множества, не являющиеся предельными, называются изолированными.