Властивості власних чисел та власних функцій задачі Штурма – Ліувіля

[1, стор. 341 - 343]

Теоремою 2 установлена еквівалентність задачі Штурма - Ліувіля (5.16) і задачі на власні значення для однорідного інтегрального рівняння (5.14’) з ермітовим неперервним ядром . При цьому власні значення задачі (5.16) пов’язані з характеристичними числами ядра співвідношенням , а відповідні їм власні функції співпадають. Тому для задачі Штурма - Ліувіля справедливі всі положення теорії інтегральних рівнянь з ермітовим неперервним ядром.

А саме:

• множина власних чисел не порожня та немає скінчених граничних точок;

• всі власні числа дійсні та мають скінчену кратність;

• власні функції

• всі 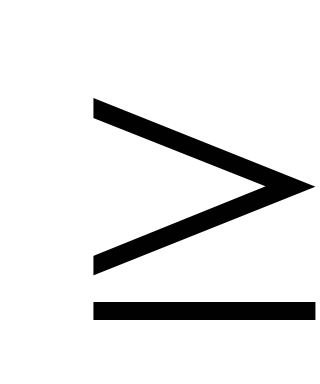0;

Останнє твердження випливає з невід’ємності диференціального оператора Штурма – Ліувілля з відповідними граничними умовами, для цього оператора всі власні функції, що відповідають різним власним значенням, ортогональні.

• множина власних чисел злічена (не може бути скінчена);

• кожне власне число має одиничну кратність;

Справді, нехай та – власні функції, які відповідають власному значенню . З граничної умови запишемо:

- розглядатиме ці співвідношення як систему лінійних рівнянь відносно . Визначник системи співпадає за величиною з визначником Вронського = -w(0) 0, враховуючи лінійну незалежність власних функцій. Звідси випливає, що розв’язок лінійної системи тривіальний, тобто , що суперечить припущенню _.

Тому ці розв’язки лінійно залежні. Це і означає, що має одиничну кратність, тобто просте.

Теорема 2 (Стеклова про розвинення в ряд Фур’є) Будь – яка функція розкладається в ряд Фур’є за ортонормованою системою власних функцій задачі Штурма –Ліувіля (5.18) І цей ряд збігається абсолютно і рівномірно.

Для коефіцієнтів Фур’є має місце рівність Парсеваля - Стєклова (5.19) та нерівність Бесселя (5.20).

_{Приклад Знайти розв’язок задачі Штурма - Ліувілля}

Розв’язання:

Для знаходження власних чисел і власних функцій розглянемо можливі значення параметру , який може приймати лише дійсні значення.

1. , .

Враховуючи граничні умови, маємо систему рівнянь Визначник цієї системи повинен дорівнювати нулю.

. Єдиним розв’язком цього рівняння є , яке не задовольняє припущенням, бо . Це означає, що система рівнянь має тривіальний розв’язок і будь – яке не є власним числом.

2. , . З граничних умов маємо, що . Тобто не є власним числом.

3. ,

Враховуючи граничні умови, маємо систему рівнянь

Визначник цієї системи прирівняємо до нуля . Це рівняння має зліченну множину розв’язків . Система лінійних алгебраїчних рівнянь має розв’язок .

Таким чином нормовані власні функції задачі Штурма – Ліувілля мають вигляд .

§6. Коливання скінченої струни. Метод відокремлення змінних (Метод Фур’є)

Розглянемо задачу: вивчити процес вільних коливань однорідної струни довжини , нерухомо закріпленої на кінцях, якщо в початковий момент часу зміщення точок струни від їх прямолінійного положення рівне , а їх початкова швидкість рівна .

Із сформульованої задачі випливає, що необхідно знайти розв’язок диференціального рівняння

, (6.1)

який задовольняє початкові умови

(6.2)

і крайові умови

(6.3)

В силу умов узгодженості

(6.4)

Наведемо спочатку формальну схему методу побудови розв’язку мішаної задачі (6.1)-(6.3). Для цього шукаємо нетривіальні розв’язки рівняння (6.1), які задовольняють крайові умови (6.3), у вигляді

(6.5)

Підставивши (6.5) у рівняння (6.1) і розділивши змінні, одержимо

Функція (6.5) буде розв’язком рівняння (6.1), якщо остання рівність виконується тотожно в області Але ліва частина цієї рівності є функцією тільки від , а права – тільки від . Зафіксувавши аргумент (або ), в лівій (правій) частині рівності одержимо сталу, а отже, для всіх (або ) права (ліва) частина стала. Таким чином, остання рівність можлива тоді і тільки тоді, коли

звідки маємо

, (6.6)

. (6.7)

Підставивши (6.5) у крайові умови (6.3), одержимо

Оскільки то із останніх рівностей маємо

(6.8)

Таким чином, нам потрібно знайти ненульові розв’язки рівняння (6.6) і крайової задачі (6.7), (6.8). Задача (6.7), (6.8) не для всяких має нетривіальні розв’язки. Задача (6.7), (6.8) – відома нам задача Штурма - Ліувілля.

, (6.9)

Знайденим власним значенням відповідають власні функції (6.10), які визначаються з точністю до сталого множника. З (6.6) отримаємо

Згідно з (6.5) функції

задовольняють рівняння (6.1) і крайові умови (6.3) при довільних і .

Розглянемо ряд (6.11)

Припустимо, що ряд (6.11) збігається і його можна почленно диференціювати два рази по і два рази по в області . Тоді ряд (6.11) буде розв’язком рівняння (6.1), який, очевидно, задовольняє і крайові умови (6.3).

Для побудови розв’язку мішаної задачі (6.1)-(6.3) залишилось у ряді (6.11) так вибрати коефіцієнти і , щоб він задовольняв і початкові умови (6.2). З цією метою підставимо ряд (6.11) у початкові умови (6.2). Одержимо

(6.12)

Нехай функції і є кусково-диференційовними на проміжку

. Тоді їх можна розкласти в ряди Фур’є

(6.13)

де

Порівнюючи ряди (6.12), (6.13), одержуємо

Підставивши знайдені коефіцієнти у (6.11), одержимо розв’язок задачі (6.1) - (6.3):

(6.14)

Вперше приведену схему побудови розв’язку задачі (6.1)-(6.3) запропонував французький математик Жан Фур’є і опублікував її у 1822р. в монографії “Аналітична теорія тепла”. Тому в літературі метод відокремлення змінних часто називають методом Фур’є.