9 |
1.6 Invariance of the interval |
1.6 I n va r i a n ce o f t h e i n t e r va l
We have, of course, not quite finished the construction of O¯ ’s coordinates. We have the position of his axes but not the length scale along them. We shall find this scale by proving what is probably the most important theorem of SR, the invariance of the interval.
Consider two events on the world line of the same light beam, such as E and P in Fig. 1.4. The differences ( t, x, y, z) between the coordinates of E and P in some frame O satisfy the relation ( x)2 + ( y)2 + ( z)2 − ( t)2 = 0, since the speed of light is 1. But by the universality of the speed of light, the coordinate differences between the same two events in the coordinates of O¯ ( ¯t, x¯, y¯, z¯) also satisfy ( x¯)2 + ( y¯)2 + ( z¯)2 − ( ¯t)2 = 0. We shall define the interval between any two events (not necessarily on the same light beam’s world line) that are separated by coordinate increments ( t, x, y, z) to be6
s2 = −( t)2 + ( x)2 + ( y)2 + ( z)2. |
(1.1) |
It follows that if s2 = 0 for two events using their coordinates in O, then s¯2 = 0 for the same two events using their coordinates in O¯ . What does this imply about the relation between the coordinates of the two frames? To answer this question, we shall assume that the relation between the coordinates of O and O¯ is linear and that we choose their origins to coincide (i.e. that the events ¯t = x¯ = y¯ = z¯ = 0 and t = x = y = z = 0 are the same). Then in the expression for s¯2,
s¯2 = −( ¯t)2 + ( x¯)2 + ( y¯)2 + ( z¯)2,
the numbers ( ¯t, x¯, which means that s¯2 can therefore write
y¯, z¯) are linear combinations of their unbarred counterparts, is a quadratic function of the unbarred coordinate increments. We
3 |
3 |
|
|
|
|
s¯2 = |
Mαβ ( xα )( xβ ) |
(1.2) |
α=0 β=0
for some numbers {Mαβ ; α, β = 0, . . . , 3}, which may be functions of v, the relative velocity of the two frames. Note that we can suppose that Mαβ = Mβα for all α and β, since only the sum Mαβ + Mβα ever appears in Eq. (1.2) when α =β. Now we again suppose that s2 = 0, so that from Eq. (1.1) we have
t = r, r = [( x)2 + ( y)2 + ( z)2]1/2.
6The student to whom this is new should probably regard the notation s2 as a single symbol, not as the square
of a quantity s. Since s2 can be either positive or negative, it is not convenient to take its square root. Some authors do, however, call s2 the ‘squared interval’, reserving the name ‘interval’ for s = √( s2). Note also that the notation s2 never means (s2).
10 |
Special relativity |
(We have supposed t > 0 for convenience.) Putting this into Eq. (1.2) gives
s¯2 = M00 |
( r)2 + 2 |
3 |
M0i xi |
r |
|
|
|
|
|
|
|
|
3 |
3 |
i=1 |
|
|
|
|
|
|
||
+ |
|
Mij xi xj. |
(1.3) |
||
i=1 j=1
But we have already observed that s¯2 must vanish if s2 does, and this must be true for arbitrary { xi, i = 1, 2, 3}. It is easy to show (see Exer. 8, § 1.14) that this implies
M0i = 0 |
i = 1, 2, 3 |
(1.4a) |
|
and |
|
|
|
Mij = −(M00)δij |
(i, j = 1, 2, 3), |
(1.4b) |
|
where δij is the Kronecker delta, defined by |
|
|
|
1 |
if i |
j, |
(1.4c) |
δij = 0 |
if i |
= j. |
|
|
|
= |
|
From this and Eq. (1.2) we conclude that
s¯2 = M00[( t)2 − ( x)2 − ( y)2 − ( z)2].
If we define a function
φ(v) = −M00,
then we have proved the following theorem: The universality of the speed of light implies that the intervals s2 and s¯2 between any two events as computed by different observers satisfy the relation
s¯2 = φ(v) s2. |
(1.5) |
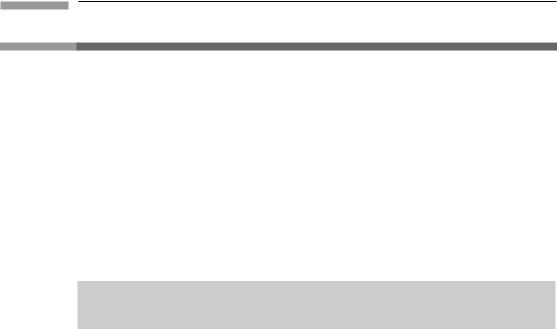
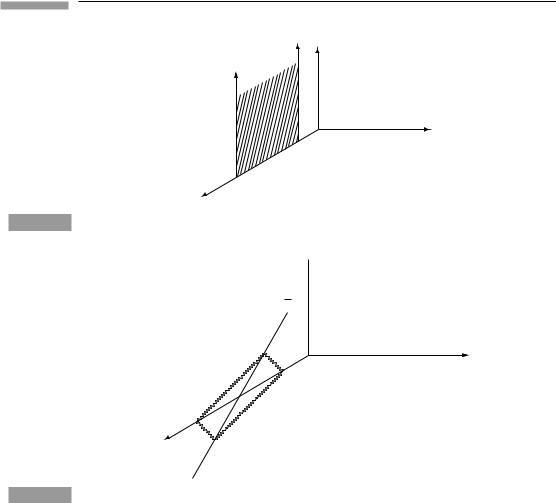
We shall now show that, in fact, φ(v) = 1, which is the statement that the interval is independent of the observer. The proof of this has two parts. The first part shows that φ(v) depends only on |v|. Consider a rod which is oriented perpendicular to the velocity v of O¯ relative to O. Suppose the rod is at rest in O, lying on the y axis. In the spacetime diagram of O (Fig. 1.6), the world lines of its ends are drawn and the region between shaded. It is easy to see that the square of its length is just the interval between the two events A and B that are simultaneous in O (at t = 0) and occur at the ends of the rod. This is because, for these events, ( x)AB = ( z)AB = ( t)AB = 0. Now comes the key point of the first part of the proof: the events A and B are simultaneous as measured by O¯ as well. The reason is most easily seen by the construction shown in Fig. 1.7, which is the same spacetime diagram as Fig. 1.6, but in which the world line of a clock in O¯ is drawn. This line is perpendicular to the y axis and parallel to the t − x plane, i.e. parallel to the ¯t axis shown in Fig. 1.5(a).
Suppose this clock emits light rays at event P which reach events A and B. (Not every clock can do this, so we have chosen the one clock in O¯ which passes through the y axis
11
Figure 1.6
Figure 1.7
1.6 Invariance of the interval
|
rod |
|
|
of |
|
|
ends |
t |
|
of |
|
World |
lines |
|
|
|
x
y
A rod at rest in O, lying on the y-axis.
t
Clock in
x
y
A clock of O¯ ’s frame, moving in the x-direction in O’s frame.
at t = 0 and can send out such light rays.) The light rays reflect from A and B, and we can see from the geometry (if you can allow for the perspective in the diagram) that they arrive back at O¯ ’s clock at the same event L. Therefore, from O¯ ’s point of view, the two events occur at the same time. (This is the same construction we used to determine the x¯ axis.) But if A and B are simultaneous in O¯ , then the interval between them in O¯ is also the square of their length in O¯ . The result is:
(length of rod in O¯ )2 = φ(v)(length of rod in O)2.
On the other hand, the length of the rod cannot depend on the direction of the velocity, because the rod is perpendicular to it and there are no preferred directions of motion (the principle of relativity). Hence the first part of the proof concludes that
φ(v) = φ(|v|). |
(1.6) |
12 |
|
|
|
|
|
|
Special relativity |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The second step of the proof is easier. It uses the principle of relativity to show that |
|||||||||
|
|
||||||||||
| |
| |
) |
= |
|
O |
O |
O |
O |
|||
|
φ( |
v |
|
1. Consider three frames, |
|
, ¯ , and |
|
. Frame |
¯ moves with speed v in, say, the |
||
|
x direction relative to O. Frame O moves with speed v in the negative x direction relative |
||||||||||
|
|
O |
|
|
O |
|
|
O |
, but for the sake of clarity we shall keep |
||
|
to |
¯ . It is clear that is in fact identical to |
|
||||||||
separate notation for the moment. We have, from Eqs. (1.5) and (1.6),
s2s¯2
=φ(v) s¯2 |
s2 |
= [φ(v)]2 s2. |
φ(v) s2 |
|
|
=
|
s |
2 |
and s |
2 |
are equal. It follows that |
But since O and O are identical, |
|
|
|
φ(v) = ±1.
We must choose the plus sign, since in the first part of this proof the square of the length of a rod must be positive. We have, therefore, proved the fundamental theorem that the interval between any two events is the same when calculated by any inertial observer:
s¯2 = s2. |
(1.7) |
Notice that from the first part of this proof we can also conclude now that the length of a rod oriented perpendicular to the relative velocity of two frames is the same when measured by either frame. It is also worth reiterating that the construction in Fig. 1.7 proved a related result, that two events which are simultaneous in one frame are simultaneous in any frame moving in a direction perpendicular to their separation relative to the first frame.
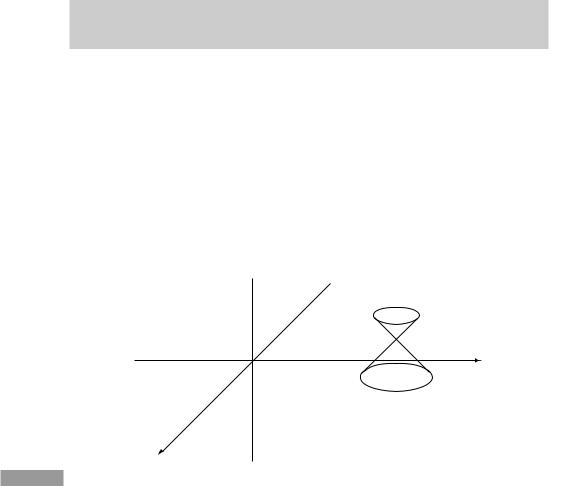
Because s2 is a property only of the two events and not of the observer, it can be used to classify the relation between the events. If s2 is positive (so that the spatial increments dominate t), the events are said to be spacelike separated. If s2 is negative, the events are said to be timelike separated. If s2 is zero (so the events are on the same light path), the events are said to be lightlike or null separated.
t 
x
|
y |
Figure 1.8 |
The light cone of an event. The z-dimension is suppressed. |
13 |
1.6 Invariance of the interval |
The events that are lightlike separated from any particular event A, lie on a cone whose apex is A. This cone is illustrated in Fig. 1.8. This is called the light cone of A. All events within the light cone are timelike separated from A; all events outside it are spacelike separated. Therefore, all events inside the cone can be reached from A on a world line which everywhere moves in a timelike direction. Since we will see later that nothing can move faster than light, all world lines of physical objects move in a timelike direction. Therefore, events inside the light cone are reachable from A by a physical object, whereas those outside are not. For this reason, the events inside the ‘future’ or ‘forward’ light cone are sometimes called the absolute future of the apex; those within the ‘past’ or ‘backward’ light cone are called the absolute past; and those outside are called the absolute elsewhere. The events on the cone are therefore the boundary of the absolute past
Figure 1.9
Galileo: |
t |
|
|
event |
|
||||
|
Future of |
|||
‘Now’ for
|
event |
|
Past of event
x
Einstein: |
t |
|
Future |
|
|
|
|
|
of |
|
|
‘Elsewhere’ |
|
‘Elsewhere’ |
|||
of |
|
|
|||
|
of |
||||
‘Now’ is only |
|
|
|||
|
|
|
|
||
itself |
|
|
Past of |
|
|
x
|
Common |
Two events: |
t future |
Future
of
Future
of
Past of
x
Past of
Common past
Old and new concepts of spacetime
14 |
Special relativity |
and future. Thus, although ‘time’ and ‘space’ can in some sense be transformed into one another in SR, it is important to realize that we can still talk about ‘future’ and ‘past’ in an invariant manner. To Galileo and Newton the past was everything ‘earlier’ than now; all of spacetime was the union of the past and the future, whose boundary was ‘now’. In SR, the past is only everything inside the past light cone, and spacetime has three invariant divisions: SR adds the notion of ‘elsewhere’. What is more, although all observers agree on what constitutes the past, future, and elsewhere of a given event (because the interval is invariant), each different event has a different past and future; no two events have identical pasts and futures, even though they can overlap. These ideas are illustrated in Fig. 1.9.
1.7 I n va r i a n t h y p e r b o l a e
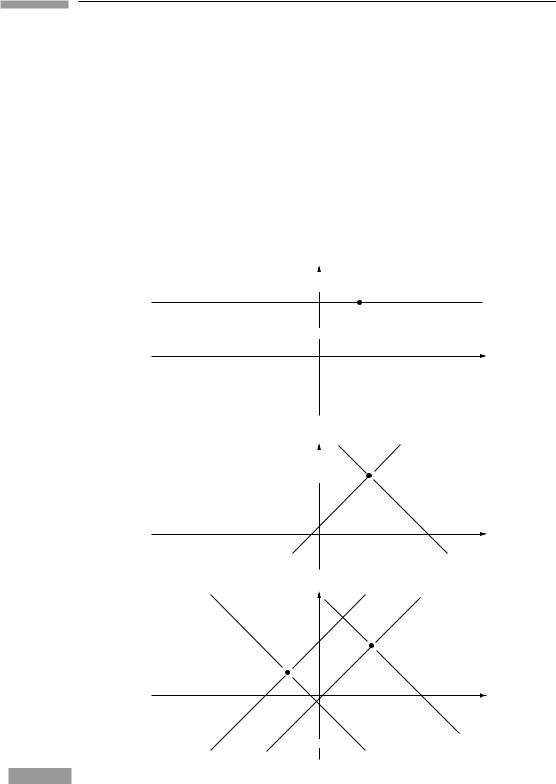
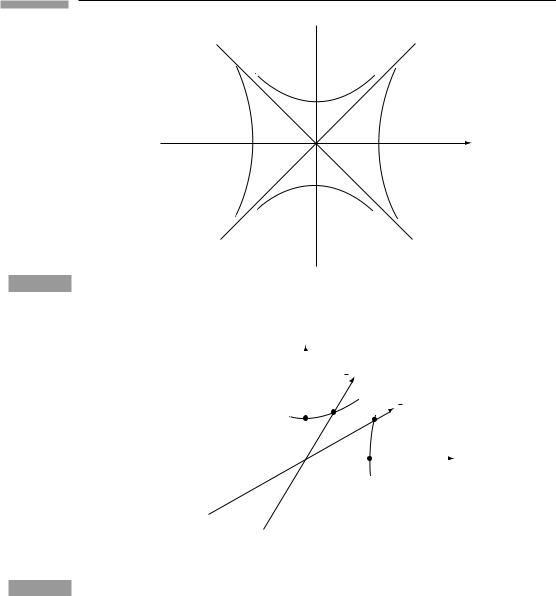
We can now calibrate the axes of O¯ ’s coordinates in the spacetime diagram of O, Fig. 1.5. We restrict ourselves to the t − x plane. Consider a curve with the equation
−t2 + x2 = a2,
where a is a real constant. This is a hyperbola in the spacetime diagram of O, and it passes through all events whose interval from the origin is a2. By the invariance of the interval, these same events have interval a2 from the origin in O¯ , so they also lie on the curve −¯t2 + x¯2 = a2. This is a hyperbola spacelike separated from the origin. Similarly, the events on the curve
−t2 + x2 = −b2
all have timelike interval −b2 from the origin, and also lie on the curve −¯t2 + x¯2 = −b2. These hyperbolae are drawn in Fig. 1.10. They are all asymptotic to the lines with slope
±1, which are of course the light paths through the origin. In a three-dimensional diagram (in which we add the y axis, as in Fig. 1.8), hyperbolae of revolution would be asymptotic to the light cone.
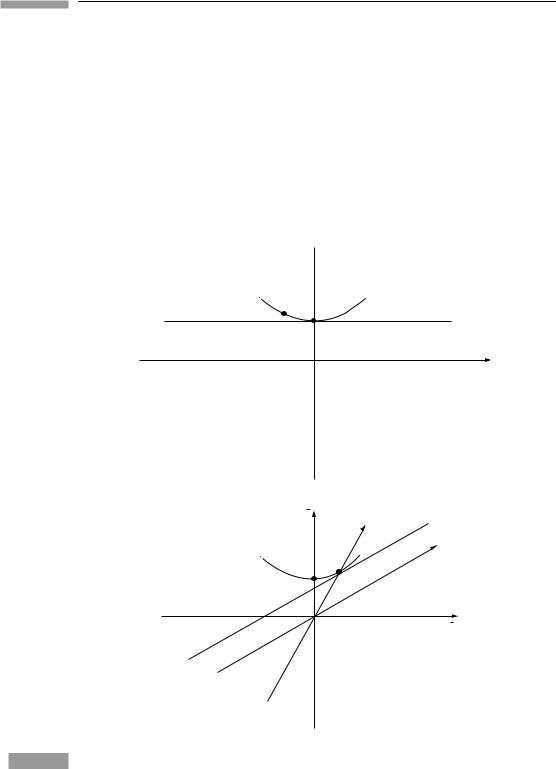
We can now calibrate the axes of O¯ . In Fig. 1.11 the axes of O and O¯ are drawn, along with an invariant hyperbola of timelike interval −1 from the origin. Event A is on the t axis, so has x = 0. Since the hyperbola has the equation
−t2 + x2 = −1,
it follows that event A has t = 1. Similarly, event B lies on the ¯t axis, so has x¯ = 0. Since the hyperbola also has the equation
−¯t2 + x¯2 = −1,
it follows that event B has ¯t = 1. We have, therefore, used the hyperbolae to calibrate the ¯t axis. In the same way, the invariant hyperbola
−t2 + x2 = 4
15 |
1.7 Invariant hyperbolae |
t 
b
–a |
a |
x |
–b
Figure 1.10
Figure 1.11
Invariant hyperbolae, for a > b.
t |
|
t |
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
Using the hyperbolae through events A and E to calibrate the x¯ and t¯ axes.
shows that event E has coordinates t = 0, x = 2 and that event F has coordinates ¯t = 0, x¯ = 2. This kind of hyperbola calibrates the spatial axes of O¯ .
Notice that event B looks to be ‘further’ from the origin than A. This again shows the inappropriateness of using geometrical intuition based upon Euclidean geometry. Here the important physical quantity is the interval −( t)2 + ( x)2, not the Euclidean distance ( t)2 + ( x)2. The student of relativity has to learn to use s2 as the physical measure of ‘distance’ in spacetime, and he has to adapt his intuition accordingly. This is not, of course, in conflict with everyday experience. Everyday experience asserts that ‘space’ (e.g. the
16 |
Special relativity |
section of spacetime with t = 0) is Euclidean. For events that have t = 0 (simultaneous to observer O), the interval is
s2 = ( x)2 + ( y)2 + ( z)2.
This is just their Euclidean distance. The new feature of SR is that time can (and must) be brought into the computation of distance. It is not possible to define ‘space’ uniquely since different observers identify different sets of events to be simultaneous (Fig. 1.5). But there is still a distinction between space and time, since temporal increments enter s2 with the opposite sign from spatial ones.
t 
x
(a) |
|
t |
t |
|
|
|
x |
|
|
|
|
|
x |
(b) |
|
Figure 1.12 (a) A line of simultaneity in O is tangent to the hyperbola at P. (b) The same tangency as seen by O¯ .