
- •Contents
- •Preface to the second edition
- •Preface to the first edition
- •1 Special relativity
- •1.2 Definition of an inertial observer in SR
- •1.4 Spacetime diagrams
- •1.6 Invariance of the interval
- •1.8 Particularly important results
- •Time dilation
- •Lorentz contraction
- •Conventions
- •Failure of relativity?
- •1.9 The Lorentz transformation
- •1.11 Paradoxes and physical intuition
- •The problem
- •Brief solution
- •2 Vector analysis in special relativity
- •Transformation of basis vectors
- •Inverse transformations
- •2.3 The four-velocity
- •2.4 The four-momentum
- •Conservation of four-momentum
- •Scalar product of two vectors
- •Four-velocity and acceleration as derivatives
- •Energy and momentum
- •2.7 Photons
- •No four-velocity
- •Four-momentum
- •Zero rest-mass particles
- •3 Tensor analysis in special relativity
- •Components of a tensor
- •General properties
- •Notation for derivatives
- •Components
- •Symmetries
- •Circular reasoning?
- •Mixed components of metric
- •Metric and nonmetric vector algebras
- •3.10 Exercises
- •4 Perfect fluids in special relativity
- •The number density n
- •The flux across a surface
- •Number density as a timelike flux
- •The flux across the surface
- •4.4 Dust again: the stress–energy tensor
- •Energy density
- •4.5 General fluids
- •Definition of macroscopic quantities
- •First law of thermodynamics
- •The general stress–energy tensor
- •The spatial components of T, T ij
- •Conservation of energy–momentum
- •Conservation of particles
- •No heat conduction
- •No viscosity
- •Form of T
- •The conservation laws
- •4.8 Gauss’ law
- •4.10 Exercises
- •5 Preface to curvature
- •The gravitational redshift experiment
- •Nonexistence of a Lorentz frame at rest on Earth
- •The principle of equivalence
- •The redshift experiment again
- •Local inertial frames
- •Tidal forces
- •The role of curvature
- •Metric tensor
- •5.3 Tensor calculus in polar coordinates
- •Derivatives of basis vectors
- •Derivatives of general vectors
- •The covariant derivative
- •Divergence and Laplacian
- •5.4 Christoffel symbols and the metric
- •Calculating the Christoffel symbols from the metric
- •5.5 Noncoordinate bases
- •Polar coordinate basis
- •Polar unit basis
- •General remarks on noncoordinate bases
- •Noncoordinate bases in this book
- •5.8 Exercises
- •6 Curved manifolds
- •Differential structure
- •Proof of the local-flatness theorem
- •Geodesics
- •6.5 The curvature tensor
- •Geodesic deviation
- •The Ricci tensor
- •The Einstein tensor
- •6.7 Curvature in perspective
- •7 Physics in a curved spacetime
- •7.2 Physics in slightly curved spacetimes
- •7.3 Curved intuition
- •7.6 Exercises
- •8 The Einstein field equations
- •Geometrized units
- •8.2 Einstein’s equations
- •8.3 Einstein’s equations for weak gravitational fields
- •Nearly Lorentz coordinate systems
- •Gauge transformations
- •Riemann tensor
- •Weak-field Einstein equations
- •Newtonian limit
- •The far field of stationary relativistic sources
- •Definition of the mass of a relativistic body
- •8.5 Further reading
- •9 Gravitational radiation
- •The effect of waves on free particles
- •Measuring the stretching of space
- •Polarization of gravitational waves
- •An exact plane wave
- •9.2 The detection of gravitational waves
- •General considerations
- •Measuring distances with light
- •Beam detectors
- •Interferometer observations
- •9.3 The generation of gravitational waves
- •Simple estimates
- •Slow motion wave generation
- •Exact solution of the wave equation
- •Preview
- •Energy lost by a radiating system
- •Overview
- •Binary systems
- •Spinning neutron stars
- •9.6 Further reading
- •10 Spherical solutions for stars
- •The metric
- •Physical interpretation of metric terms
- •The Einstein tensor
- •Equation of state
- •Equations of motion
- •Einstein equations
- •Schwarzschild metric
- •Generality of the metric
- •10.5 The interior structure of the star
- •The structure of Newtonian stars
- •Buchdahl’s interior solution
- •10.7 Realistic stars and gravitational collapse
- •Buchdahl’s theorem
- •Quantum mechanical pressure
- •White dwarfs
- •Neutron stars
- •10.9 Exercises
- •11 Schwarzschild geometry and black holes
- •Black holes in Newtonian gravity
- •Conserved quantities
- •Perihelion shift
- •Post-Newtonian gravity
- •Gravitational deflection of light
- •Gravitational lensing
- •Coordinate singularities
- •Inside r = 2M
- •Coordinate systems
- •Kruskal–Szekeres coordinates
- •Formation of black holes in general
- •General properties of black holes
- •Kerr black hole
- •Dragging of inertial frames
- •Ergoregion
- •The Kerr horizon
- •Equatorial photon motion in the Kerr metric
- •The Penrose process
- •Supermassive black holes
- •Dynamical black holes
- •11.6 Further reading
- •12 Cosmology
- •The universe in the large
- •The cosmological arena
- •12.2 Cosmological kinematics: observing the expanding universe
- •Homogeneity and isotropy of the universe
- •Models of the universe: the cosmological principle
- •Cosmological metrics
- •Cosmological redshift as a distance measure
- •The universe is accelerating!
- •12.3 Cosmological dynamics: understanding the expanding universe
- •Critical density and the parameters of our universe
- •12.4 Physical cosmology: the evolution of the universe we observe
- •Dark matter and galaxy formation: the universe after decoupling
- •The early universe: fundamental physics meets cosmology
- •12.5 Further reading
- •Appendix A Summary of linear algebra
- •Vector space
- •References
- •Index

5 |
Preface to curvature |
|
|
5.1 O n t h e re l a t i o n o f g ra v i t a t i o n t o c u r va t u re
Until now we have discussed only SR. In SR, forces have played a background role, and we have never introduced gravitation explicitly as a possible force. One ingredient of SR is the existence of inertial frames that fill all of spacetime: all of spacetime can be described by a single frame, all of whose coordinate points are always at rest relative to the origin, and all of whose clocks run at the same rate relative to the origin’s clock. From the fundamental postulates we were led to the idea of the interval s2, which gives an invariant geometrical meaning to certain physical statements. For example, a timelike interval between two events is the time elapsed on a clock which passes through the two events; a spacelike interval is the length of a rod that joins two events in a frame in which they are simultaneous. The mathematical function that calculates the interval is the metric, and so the metric of SR is defined physically by lengths of rods and readings of clocks. This is the power of SR and one reason for the elegance and compactness of
tensor notation in it (for instance the replacement of ‘number density’ and ‘flux’ by N). On a piece of paper on which had been plotted all the events and world lines of interest in some coordinate system, it would always be possible to define any metric by just giving its components gαβ as some arbitrarily chosen set of functions of the coordinates. But this arbitrary metric would be useless in doing physical calculations. The usefulness of ηαβ is its close relation to experiment, and our derivation of it drew heavily on the experiments.
This closeness to experiment is, of course, a test. Since ηαβ makes certain predictions about rods and clocks, we can ask for their verification. In particular, is it possible to construct a frame in which the clocks all run at the same rate? This is a crucial question, and we shall show that in a nonuniform gravitational field the answer, experimentally, is no. In this sense, gravitational fields are incompatible with global SR: the ability to construct a global inertial frame. We shall see that in small regions of spacetime – regions small enough that nonuniformities of the gravitational forces are too small to measure – we can always construct a ‘local’ SR frame. In this sense, we shall have to build local SR into a more general theory. The first step is the proof that clocks don’t all run at the same rate in a gravitational field.
112 |
Preface to curvature |
The gravitational redshift experiment
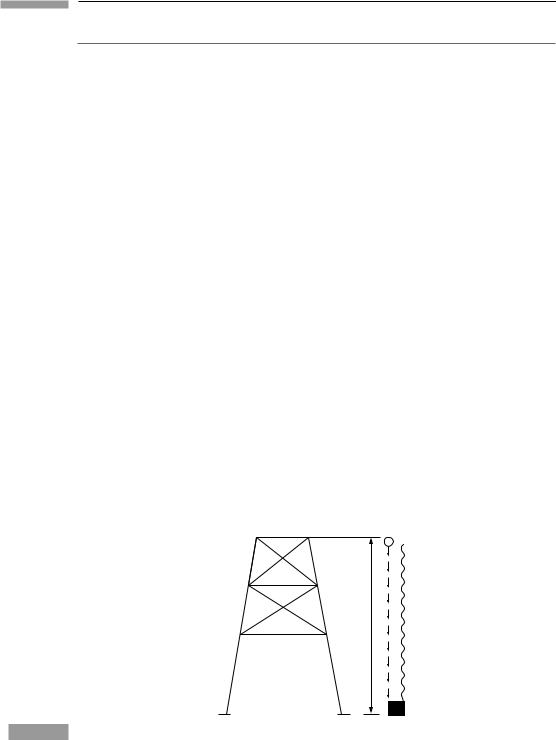
Let us first imagine performing an idealized experiment, first suggested by Einstein. (i) Let a tower of height h be constructed on the surface of Earth, as in Fig. 5.1. Begin with a particle of rest mass m at the top of the tower. (ii) The particle is dropped and falls freely with acceleration g. It reaches the ground with velocity v = (2gh)1/2, so its total energy E, as measured by an experimenter on the ground, is m + 12 mv2 + 0(v4) = m + mgh + 0(v4).
(iii)The experimenter on the ground has some magical method of changing all this energy into a single photon of the same energy, which he directs upwards. (Such a process does not violate conservation laws, since Earth absorbs the photon’s momentum but not its energy, just as it does for a bouncing rubber ball. The student skeptical of ‘magic’ should show how the argument proceeds if only a fraction ε of the energy is converted into a photon.)
(iv)Upon its arrival at the top of the tower with energy E , the photon is again magically changed into a particle of rest mass m = E . It must be that m = m; otherwise, perpetual
motion could result by the gain in energy obtained by operating such an experiment. So we are led by our abhorrence of the injustice of perpetual motion to predict that E = m or, for
the photon,
|
E |
|
hν |
|
|
|
m |
|
|
4 |
|
|
|
E |
= |
hν |
= |
m |
+ |
mgh |
+ |
0(v4) |
= 1 − gh + 0(v |
). |
(5.1) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
We predict that a photon climbing in Earth’s gravitational field will lose energy (not surprisingly) and will consequently be redshifted.
Although our thought experiment is too idealized to be practical, it is possible to measure the redshift predicted by Eq. (5.1) directly. This was first done by Pound and Rebka (1960) and improved by Pound and Snider (1965). The experiment used the Mössbauer effect to
m
 γ
γ
h
Figure 5.1
A mass m is dropped from a tower of height h. The total mass at the bottom is converted into energy and returned to the top as a photon. Perpetual motion will be performed unless the photon loses as much energy in climbing as the mass gained in falling. Light is therefore redshifted as it climbs in a gravitational field.
113 |
5.1 On the relation of gravitation to curvature |
obtain great precision in the measurement of the difference ν − ν produced in a photon climbing a distance h = 22.5 m. Eq. (5.1) was verified to approximately 1% precision.
With improvements in technology between 1960 and 1990, the gravitational redshift moved from being a small exotic correction to becoming an effect that is central to society: the GPS navigation system incorporates vital corrections for the redshift, in the absence of which it would not remain accurate for more than a few minutes. The system uses a network of high-precision atomic clocks in orbiting satellites, and navigation by an apparatus on Earth is accomplished by reading the time-stamps on signals received from five or more satellites. But, as we shall see below, the gravitational redshift implies that time itself runs slightly faster at the higher altitude than it does on the Earth. If this were not compensated for, the ground receiver would soon get wrong time-stamps. The successful operation of GPS can be taken to be a very accurate verification of the redshift. See Ashby (2003) for a full discussion of relativity and the GPS system.
This experimental verification of the redshift is comforting from the point of view of energy conservation. But it is the death-blow to our chances of finding a simple, specialrelativistic theory of gravity, as we shall now show.
Nonexistence of a Lorentz frame at rest on Earth
Figure 5.2
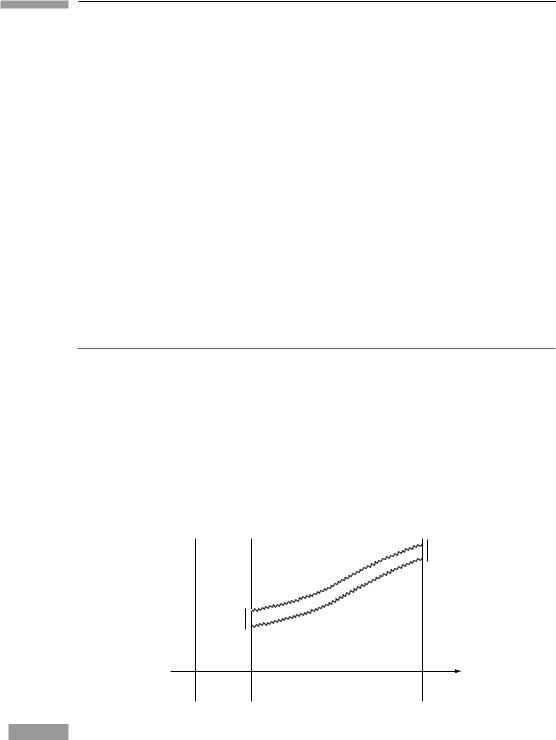
If SR is to be valid in a gravitational field, it is a natural first guess to assume that the ‘laboratory’ frame at rest on Earth is a Lorentz frame. The following argument, due originally to Schild (1967), easily shows this assumption to be false. In Fig. 5.2 we draw a spacetime diagram in this hypothetical frame, in which the one spatial dimension plotted is the vertical one. Consider light as a wave, and look at two successive ‘crests’ of the wave as they move upward in the Pound–Rebka–Snider experiment. The top and bottom of the tower have vertical world lines in this diagram, since they are at rest. Light is shown moving on a wiggly line, and it is purposely drawn curved in some arbitrary way. This is to allow for the possibility that gravity may act on light in an unknown way, deflecting
t 
tbot
|
Second |
crest |
|
|
|
|
|
tbot |
First |
crest |
|
|
|||
z
Bottom |
Top |
In a time-independent gravitational field, two successive ‘crests’ of an electromagnetic wave must travel identical paths. Because of the redshift (Eq. (5.1)) the time between them at the top is larger than at the bottom. An observer at the top therefore ‘sees’ a clock at the bottom running slowly.

114 |
Preface to curvature |
it from a null path. But no matter how light is affected by gravity the effect must be the same on both wave crests, since the gravitational field does not change from one time to another. Therefore the two crests’ paths are congruent, and we conclude from the hypothetical Minkowski geometry that ttop = tbottom. On the other hand, the time between two crests is simply the reciprocal of the measured frequency t = 1/ν. Since the Pound– Rebka–Snider experiment establishes that νbottom > νtop, we know that ttop > tbottom. The conclusion from Minkowski geometry is wrong, and the reference frame at rest on Earth is not a Lorentz frame.
Is this the end, then, of SR? Not quite. We have shown that the Lorentz frame at rest on Earth is not inertial. We have not shown that there are no inertial frames. In fact there are certain frames which are inertial in a restricted sense, and in the next paragraph we shall use another physical argument to find them.
The principle of equivalence
One important property of an inertial frame is that a particle at rest in it stays at rest if no forces act on it. In order to use this, we must have an idea of what a force is. Ordinarily, gravity is regarded as a force. But, as Galileo demonstrated in his famous experiment at the Leaning Tower of Pisa, gravity is distinguished from all other forces in a remarkable way: all bodies given the same initial velocity follow the same trajectory in a gravitational field, regardless of their internal composition. With all other forces, some bodies are affected and others are not: electromagnetism affects charged particles but not neutral ones, and the trajectory of a charged particle depends on the ratio of its charge to its mass, which is not the same for all particles. Similarly, the other two basic forces in physics – the so-called ‘strong’ and ‘weak’ interactions – affect different particles differently. With all these forces, it would always be possible to define experimentally the trajectory of a particle unaffected by the force, i.e. a particle that remained at rest in an inertial frame. But, with gravity, this does not work. Attempting to define an inertial frame at rest on Earth, then, is vacuous, since no free particle (not even a photon) could possibly be a physical ‘marker’ for it.
But there is a frame in which particles do keep a uniform velocity. This is a frame which falls freely in the gravitational field. Since this frame accelerates at the same rate as free particles do (at least the low-velocity particles to which Newtonian gravitational physics applies), it follows that all such particles will maintain a uniform velocity relative to this frame. This frame is at least a candidate for an inertial frame. In the next section we will show that photons are not redshifted in this frame, which makes it an even better candidate. Einstein built GR by taking the hypothesis that these frames are inertial.
The argument we have just made, that freely falling frames are inertial, will perhaps be more familiar to the student if it is turned around. Consider, in empty space free of gravity, a uniformly accelerating rocket ship. From the point of view of an observer inside, it appears that there is a gravitational field in the rocket: objects dropped accelerate toward the rear of the ship, all with the same acceleration, independent of their internal composition.1
1This has been tested experimentally to extremely high precision in the so-called Eötvös experiment. See Dicke (1964).
