Свойства плотности вероятности нормального распределения
Рассмотрим свойства плотности вероятности СВ X, распределенных по нормаль-ному закону с параметрамиaи.
График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса).
Исследуем функцию
,
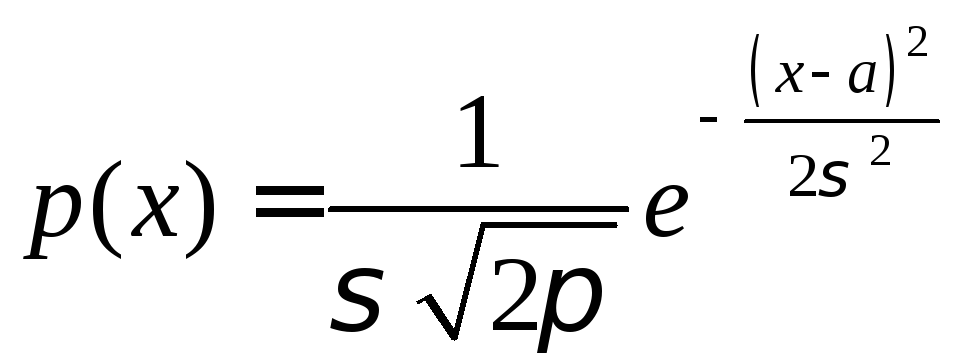где>0.
методом дифференциального исчисления.
1). Функция определена на всей числовой
оси Ox., т.е.
.
2). При всех значениях xфункция принимает положительные значения, т.е. нормальная кривая расположена выше осиOx.
3).
,
т.е. осьOxслужит
горизонтальной асимптотой графика.
4). Исследуем функцию на экстремум. Найдем первую производную:
.
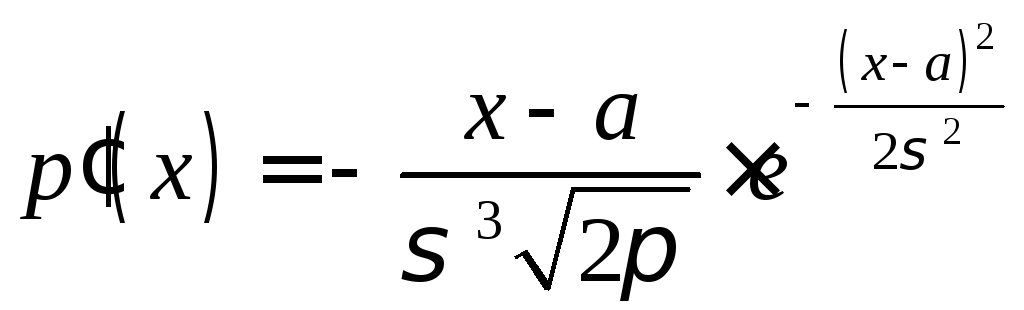Легко видеть, что
приx=a,
приx<a,
приx>a.
Следовательно, при x=aфункция имеет максимум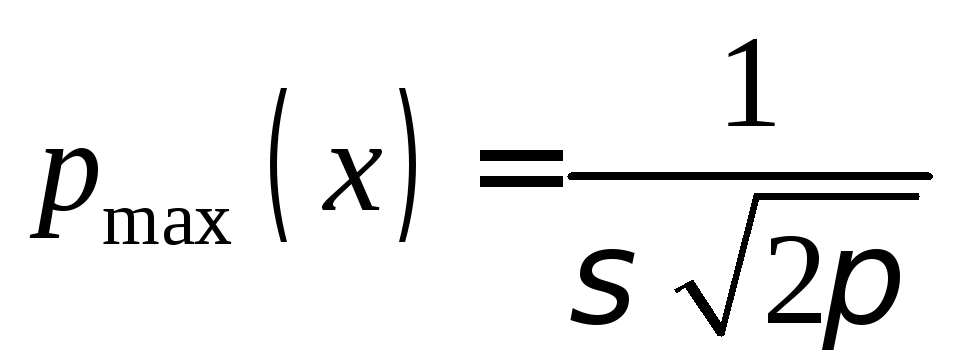
.
5). Разность xaсодержится в аналитическом выражении в квадрате, т.е. график функции симметричен относительно прямойx=a.
6). Исследуем функцию на точки перегиба. Найдем вторую производную:
.
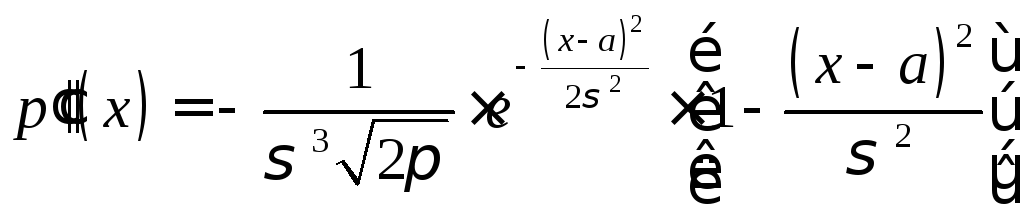Легко видеть, что при x1=aиx2=a+вторая производная равна нулю, а при
переходе через эти точки она меняет
знак. Причем значения функции в обеих
точках равны
.
Таким образом, точки графика
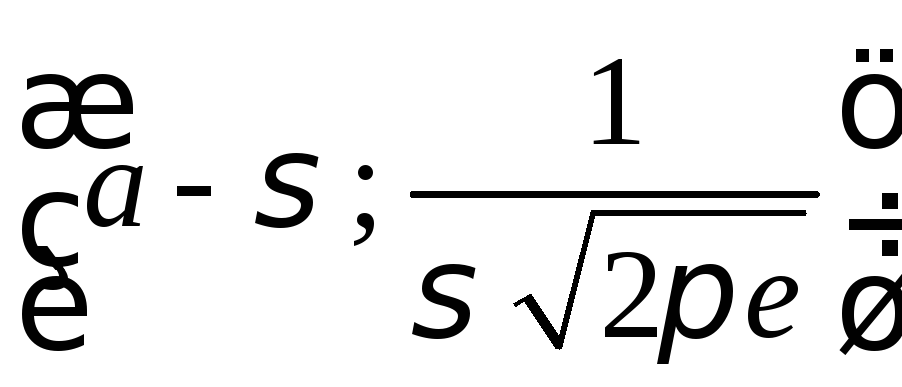и
являются точками перегиба.
Значит, график функции принимает вид
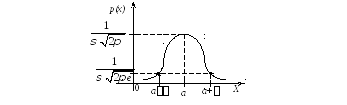
Как видно, на форму и расположение нормальной кривой влияют значения параметров aи.
Изменение величины параметра a (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ox: вправо, если a возрастает и влево, если a убывает.
С возрастанием максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ox; при убывании нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Oy.
Выше было рассмотрено, как можно найти вероятность того, что СВ X, которая распределена по нормальному закону примет значение, принадлежащее интервалу (x1;x2), и связь с интегральной функцией Лапласа:
.
(*)
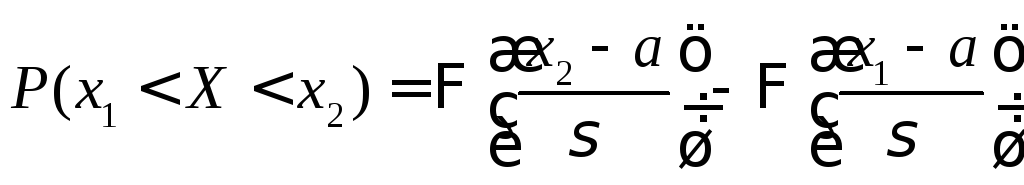Часто на практике требуется вычислить
вероятность того, что отклонение
нормально распределенной СВ Xпо абсолютной величине меньше заданного
положительного числа,
т.е. требуется найти вероятность
осуществления неравенства
.
Заменим это неравенство равносильным ему двойным неравенством
или
.
Используя формулу (*), получаем
(функция
Лапласа – нечетная)=
.
Итак, окончательно получаем
.
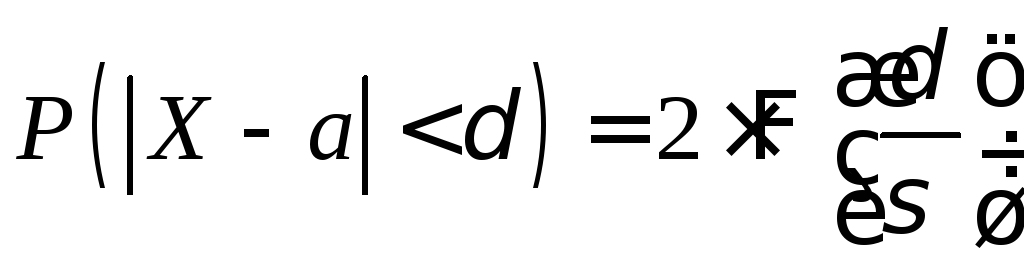(2.16)
В частности, при
.
(2.17)
Пример 2.10. Случайная величинаX распределена по нормальному закону. Математическое ожидание и дисперсия этой величины соответственно равны 20 и 100. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.
Решение.По условию
.
Следовательно,
.
Значение функции (0,3) находим по таблице значений интегральной функции Лапласа.
Далее мы рассмотрим так называемое правило «трех сигм».
Преобразуем формулу
,
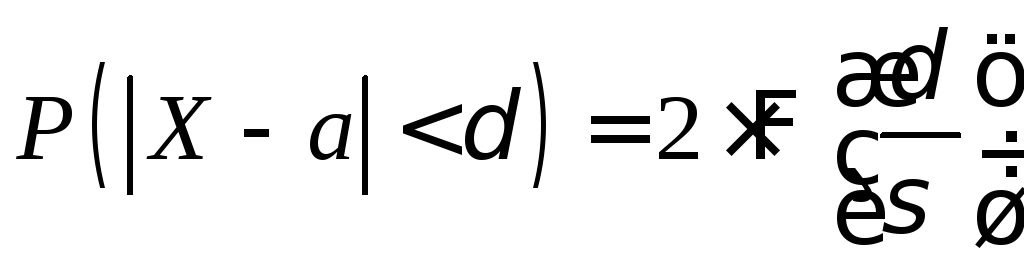положив
.
В итоге получим
.
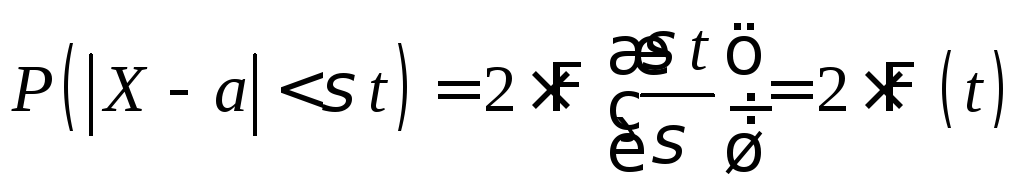Если
и, следовательно,
,
то
.
т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27 % случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
На практике правило трех сигм применяется так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то имеются основания предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.