
- •Раздел 3
- •1. Основные понятия
- •Генеральная и выборочная совокупность. Вариационный ряд
- •Эмпирическая функция распределения. Полигон. Гистограмма
- •1.3. Статистические оценки параметров распределения
- •Требования, которым должны удовлетворять оцениваемые параметры
- •2. Точечные и интервальные оценки
- •Доверительные интервалы для оценки математического ожидания нормального распределения при известном
- •Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном
- •Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения
- •3. Статистические гипотезы
- •3.1. Основные понятия
- •Критическая область. Область принятия гипотез. Критические точки
- •Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
- •Правило проверки нулевой гипотезы
- •4. Элементы теории корреляции
- •Свойства коэффициента корреляции
- •5. Элементы дисперсионного анализа
1.3. Статистические оценки параметров распределения
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение; если же есть основания считать, что признак имеет, например, распределение Пуассона, то необходимо оценить параметр , которым это распределение определяется.
Обычно в распоряжении исследователя
имеются лишь данные выборки, например,
значения количественного признака
![]() ,
полученные в результатеnнаблюдений (здесь и далее наблюдения
предполагаются независимыми). Через
эти данные и выражают оцениваемый
параметр.
,
полученные в результатеnнаблюдений (здесь и далее наблюдения
предполагаются независимыми). Через
эти данные и выражают оцениваемый
параметр.
Рассматривая
![]() как независимые случайные величины
как независимые случайные величины![]() ,
можно сказать, что найти статистическую
оценку неизвестного параметра
теоретического распределения – это
значит найти функцию от наблюдаемых
случайных величин, которая и дает
приближенное значение оцениваемого
параметра.
,
можно сказать, что найти статистическую
оценку неизвестного параметра
теоретического распределения – это
значит найти функцию от наблюдаемых
случайных величин, которая и дает
приближенное значение оцениваемого
параметра.
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.
Пусть
![]() (
(![]() «тета») есть
статистическая оценки неизвестного
параметратеоретического распределения. Допустим,
что по выборке объемаnнайдена оценка
«тета») есть
статистическая оценки неизвестного
параметратеоретического распределения. Допустим,
что по выборке объемаnнайдена оценка![]() .
Повторим опыт, т.е. извлечем из генеральной
совокупности другую выборку того же
объема и по ее данным найдем оценку
.
Повторим опыт, т.е. извлечем из генеральной
совокупности другую выборку того же
объема и по ее данным найдем оценку![]() .
Повторяя опыт многократно, получим
числа
.
Повторяя опыт многократно, получим
числа![]() ,
которые, вообще говоря, будут различны
между собой. Таким образом, оценку
,
которые, вообще говоря, будут различны
между собой. Таким образом, оценку![]() можно рассматривать как случайную
величину, а числа
можно рассматривать как случайную
величину, а числа![]() – как ее возможные значения.
– как ее возможные значения.
Представим себе, что оценка
![]() дает приближенное значениес избытком; тогда каждое, найденное по
данным выборок, число
дает приближенное значениес избытком; тогда каждое, найденное по
данным выборок, число![]() будет больше истинного значения.
Ясно, что в этом случае и математическое
ожидание (среднее значение) случайной
величины
будет больше истинного значения.
Ясно, что в этом случае и математическое
ожидание (среднее значение) случайной
величины![]() будет больше, чем,
т.е.
будет больше, чем,
т.е.![]() .
Очевидно, что если
.
Очевидно, что если![]() дает оценку с недостатком, то
дает оценку с недостатком, то![]() .
.
Таким образом, использование статистической
оценки, математическое ожидание которой
не равно оцениваемому параметру, привело
бы к систематическим (одного знака)
ошибкам. По этой причине естественно
потребовать, чтобы математическое
ожидание оценки
![]() было равно оцениваемому параметру.
было равно оцениваемому параметру.
Требования, которым должны удовлетворять оцениваемые параметры
1) Несмещенной называют
статистическую оценку![]() ,
математическое ожидание которой равно
оцениваемому параметрупри любом объеме выборки, т.е.
,
математическое ожидание которой равно
оцениваемому параметрупри любом объеме выборки, т.е.
![]() .
.
Смещеннойназывают оценку, математическое ожидание которой не равно оцениваемому параметру.
2) Эффективной называют статистическую оценку, которая (при заданном объеме выборкиn) имеет наименьшую возможную дисперсию.
3) Состоятельнойназывают
статистическую оценку, которая при![]() стремится по вероятности к оцениваемому
параметру. Например, если дисперсия
несмещенной оценки при
стремится по вероятности к оцениваемому
параметру. Например, если дисперсия
несмещенной оценки при![]() стремится к нулю, то такая оценка
оказывается и состоятельной.
стремится к нулю, то такая оценка
оказывается и состоятельной.
Введем числовые характеристики изучаемой совокупности по какому-то признаку.
Пусть изучается дискретная генеральная совокупность относительно количественного признака X.
Определение 1.11.Генеральной
средней![]() называют среднее арифметическое значений
признака генеральной совокупности.
называют среднее арифметическое значений
признака генеральной совокупности.
Если все значения
![]() признака генеральной совокупности
объемаNразличны, то
признака генеральной совокупности
объемаNразличны, то
![]() .
.
Если же значения признака
![]() имеют соответственно частоты
имеют соответственно частоты![]() причем
причем![]() ,
то
,
то
![]() .
.
т.е. генеральная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.
Пусть генеральная совокупность объема
Nсодержит объекты с
различными значениями признакаX,
равными![]() .
Величину признакаXможно рассматривать как случайную
величину, возможные значения которой
.
Величину признакаXможно рассматривать как случайную
величину, возможные значения которой![]() имеют одинаковые вероятности, равные
имеют одинаковые вероятности, равные![]() .
Найдем математическое ожиданиеM(X):
.
Найдем математическое ожиданиеM(X):
![]() .
.
Итак, можно сделать следующий вывод: если рассматривать исследуемый признак Xгенеральной совокупности как случайную величину, то математическое ожидание признака равно генеральной средней этого признака:
![]() .
.
Такой же итог будет получен, если допустить, что генеральная совокупность содержит по нескольку объектов с одинаковыми значениями признака или рассматривать генеральную совокупность с непрерывным распределением признака X.
Пусть для изучения генеральной совокупности относительно количественного признака Xизвлечена выборка объемаn.
Определение 1.12.Выборочной средней![]() называют среднее арифметическое значений
признака выборочной совокупности.
называют среднее арифметическое значений
признака выборочной совокупности.
Если все значения
![]() признака выборки объемаnразличны, то
признака выборки объемаnразличны, то
![]() .
(1.2)
.
(1.2)
Если же значения признака
![]() имеют соответственно частоты
имеют соответственно частоты![]() причем
причем![]() ,
то
,
то
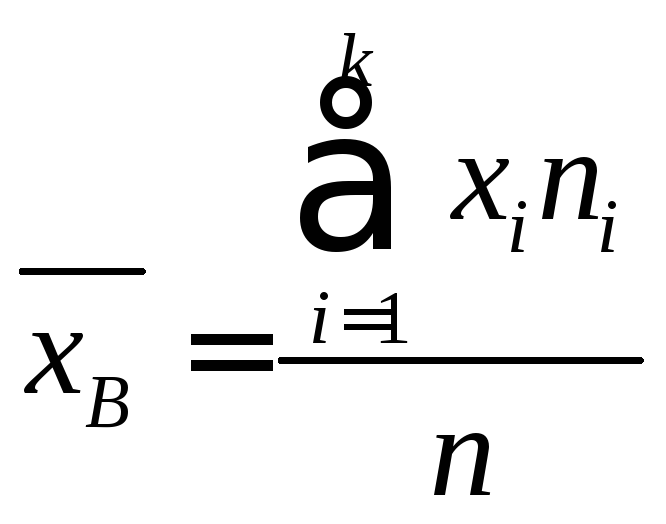 .
(1.3)
.
(1.3)
т.е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.
Выборочная средняя, найденная по данным одной выборки есть, очевидно, определенное число. Если же извлекать другие выборки того же объема из той же генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке. Таким образом, выборочную среднюю можно рассматривать как случайную величину, а, следовательно, можно говорить о распределениях выборочной средней и о числовых характеристиках этого распределения (его называют выборочным), в частности, о математическом ожидании и дисперсии выборочного распределения.
Пусть из генеральной совокупности (в
результате независимых наблюдений над
количественным признаком X)
извлечена выборка объемаnсо значениями признака![]() .
Не уменьшая общности рассуждений, будем
считать эти значения признака различными.
Пусть генеральная средняя
.
Не уменьшая общности рассуждений, будем
считать эти значения признака различными.
Пусть генеральная средняя![]() неизвестна и требуется оценить ее по
данным выборки. В качестве оценки
генеральной средней принимают выборочную
среднюю
неизвестна и требуется оценить ее по
данным выборки. В качестве оценки
генеральной средней принимают выборочную
среднюю![]() .
.
Убедимся, что
![]() есть несмещенная оценка, т.е. покажем,
что математическое ожидание этой оценки
равно
есть несмещенная оценка, т.е. покажем,
что математическое ожидание этой оценки
равно![]() .
Будем рассматривать
.
Будем рассматривать![]() как случайную величину и
как случайную величину и![]() ,
как независимые, одинаково распределенные
случайные величины
,
как независимые, одинаково распределенные
случайные величины![]() .
Поскольку эти величины одинаково
распределены, то они имеют одинаковые
числовые характеристики, в частности,
математическое ожидание, которое
обозначим черезa. Так
как математическое ожидание среднего
арифметического одинаково распределенных
случайных величин равно математическому
ожиданию каждой из величин, то
.
Поскольку эти величины одинаково
распределены, то они имеют одинаковые
числовые характеристики, в частности,
математическое ожидание, которое
обозначим черезa. Так
как математическое ожидание среднего
арифметического одинаково распределенных
случайных величин равно математическому
ожиданию каждой из величин, то
![]() .
(*)
.
(*)
Приняв во внимание, что каждая из величин
![]() имеет то же распределение, что и
генеральная совокупность (которую мы
рассматриваем как случайную величину),
заключаем, что и числовые характеристики
этих величин и генеральной совокупности
одинаковы. В частности, математическое
ожиданиеaкаждой из
величин равно математическому ожиданию
признакаXгенеральной
совокупности, т.е.
имеет то же распределение, что и
генеральная совокупность (которую мы
рассматриваем как случайную величину),
заключаем, что и числовые характеристики
этих величин и генеральной совокупности
одинаковы. В частности, математическое
ожиданиеaкаждой из
величин равно математическому ожиданию
признакаXгенеральной
совокупности, т.е.
![]() .
.
Заменив в формуле (*) математическое
ожидание aчерез![]() ,
окончательно получаем
,
окончательно получаем
![]() .
.
Тем самым доказано, что выборочная средняя есть несмещенная оценка генеральной средней.
Легко показать, что выборочная средняя является и состоятельной оценкой генеральной средней.
Из сказанного следует также, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом и состоит свойство устойчивости выборочных средних.
Для того чтобы охарактеризовать рассеяние значений количественного признака Xгенеральной совокупности вокруг своего значения, вводят сводную характеристику – генеральную дисперсию.
Определение 1.13.Генеральной
дисперсией
![]() называют среднее арифметическое
квадратов отклонений значений признака
генеральной совокупности от их среднего
значения
называют среднее арифметическое
квадратов отклонений значений признака
генеральной совокупности от их среднего
значения![]() .
.
Если все значения
![]() признака генеральной совокупности
объемаNразличны, то
признака генеральной совокупности
объемаNразличны, то
![]() .
.
Если же значения признака
![]() имеют соответственно частоты
имеют соответственно частоты![]() причем
причем![]() ,
то
,
то
![]() .
.
т.е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Кроме дисперсии, для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением.
Определение 1.14.Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:
![]() .
.
Для того чтобы охарактеризовать рассеяние
наблюдаемых значений количественного
признака выборки вокруг своего среднего
значения
![]() вводят сводную характеристику –
выборочную дисперсию.
вводят сводную характеристику –
выборочную дисперсию.
Определение 1.15.Выборочной
дисперсией
![]() называют среднее арифметическое
квадратов отклонений наблюдаемых
значений признака от их среднего значения
называют среднее арифметическое
квадратов отклонений наблюдаемых
значений признака от их среднего значения![]() .
.
Если все значения
![]() признака выборки объемаnразличны, то
признака выборки объемаnразличны, то
![]() .
(1.4)
.
(1.4)
Если же значения признака
![]() имеют соответственно частоты
имеют соответственно частоты![]() причем
причем![]() ,
то
,
то
![]() .
(1.5)
.
(1.5)
т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Определение 1.16.Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
![]() .
(1.6)
.
(1.6)
Вычисление дисперсии, безразлично, выборочной или генеральной, можно упростить, используя следующую теорему.
Теорема 1.1.Дисперсия равна среднему квадратов значений признака минус квадрат общей средней
![]() ,
(1.7)
,
(1.7)
где
![]() ,
,![]() .
.
Кроме выборочной средней, выборочной дисперсии и выборочного среднего квадратического отклонения применяются и другие характеристики вариационного ряда. Укажем некоторые из них для дискретного вариационного ряда.
Определение 1.17.Модой Моназывают варианту, которая имеет наибольшую частоту.
Определение 1.18.Медианой Меназывают варианту, которая делит
вариационный ряд на две части, равные
по числу вариант. Если число вариант
нечетно, т.е.![]() ,
то
,
то![]() .
Если число вариант четно, то медиана
.
Если число вариант четно, то медиана![]() .
.
Определение 1.19.Размахом варьирования Rназывают разность между наибольшей и наименьшей вариантами:
![]() .
.
Определение 1.20.Коэффициентом вариации Vназывают выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней:
![]() .
.
Коэффициент вариации служит для сравнения величин рассеяния двух вариационных рядов: тот из них имеет большее рассеяние, у которого коэффициент вариации больше.
Пусть из генеральной совокупности в результате nнезависимых наблюдений над количественным признакомXизвлечена выборка объемаn:
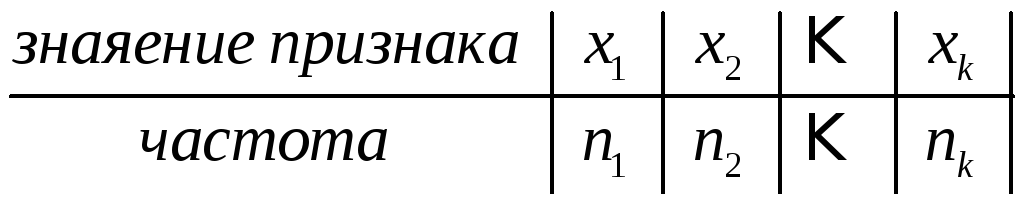 ,
,
причем
![]() .
.
Требуется по данным выборки оценить
(приближенно найти) неизвестную
генеральную дисперсию
![]() .
Если в качестве оценки генеральной
дисперсии принять выборочную дисперсию,
то эта оценка будет приводить к
систематическим ошибкам, давая заниженное
значение генеральной дисперсии.
Объясняется это тем, и это можно доказать,
что выборочная дисперсия является
смещенной оценкой
.
Если в качестве оценки генеральной
дисперсии принять выборочную дисперсию,
то эта оценка будет приводить к
систематическим ошибкам, давая заниженное
значение генеральной дисперсии.
Объясняется это тем, и это можно доказать,
что выборочная дисперсия является
смещенной оценкой
![]() ,
другими словами математическое ожидание
выборочной дисперсии не равно оцениваемой
генеральной дисперсии, а равно
,
другими словами математическое ожидание
выборочной дисперсии не равно оцениваемой
генеральной дисперсии, а равно
![]() .
.
Легко «исправить» выборочную дисперсию
так, чтобы ее математическое ожидание
было равно генеральной дисперсии.
Достаточно для этого умножить
![]() на дробь
на дробь![]() .
Сделав это, получим «исправленную
дисперсию», которую обычно обозначают
через
.
Сделав это, получим «исправленную
дисперсию», которую обычно обозначают
через![]() :
:
![]() .
.
Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии. Действительно,
![]() .
.
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию
![]() .
(1.8)
.
(1.8)
Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
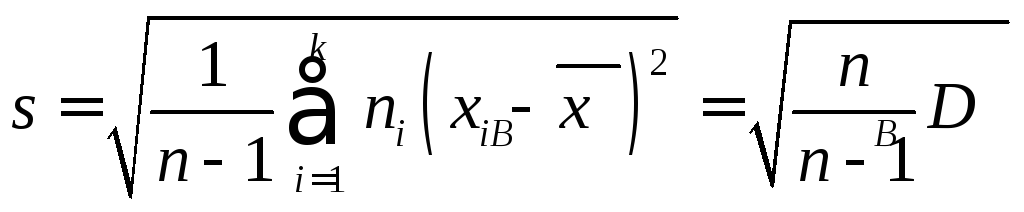 .
(1.9)
.
(1.9)
Подчеркнем, что sне является несмещенной оценкой.
Пример 1.1. В результате некоторого эксперимента были получены данные, записанные в виде статистического ряда.
|
11,2 |
12,6 |
10,9 |
10,9 |
15,1 |
14,1 |
11,5 |
15,6 |
16,1 |
13,2 |
|
16,9 |
14,9 |
16,3 |
14,4 |
14,7 |
13 |
13,1 |
11,6 |
15,9 |
17,9 |
|
18,1 |
11,1 |
15,1 |
7,8 |
16,4 |
16,5 |
11,3 |
17,1 |
15,9 |
13,2 |
|
12,7 |
17,6 |
12,4 |
18,3 |
13 |
16,3 |
11,3 |
15,7 |
19 |
16,3 |
|
18,2 |
12,1 |
14,8 |
11,5 |
13,2 |
20,3 |
11,7 |
18,7 |
11,7 |
18,7 |
Произвести статистическую обработку результатов измерений:
1) построить интервальный вариационный ряд;
2) построить гистограмму относительных частот, эмпирическую функцию распределения и ее график (кумулянту);
3) найти выборочные числовые
характеристики
![]() ;
;
Решение.
1) Сначала составляем дискретный вариационный ряд, записав варианты в порядке возрастания.
|
7,8 |
10,9 |
10,9 |
11,1 |
11,2 |
11,3 |
11,3 |
11,5 |
11,5 |
11,6 |
|
11,7 |
11,7 |
12,1 |
12,4 |
12,6 |
12,7 |
13 |
13 |
13,1 |
13,2 |
|
13,2 |
13,2 |
14,1 |
14,4 |
14,7 |
14,8 |
14,9 |
15,1 |
15,1 |
15,6 |
|
15,7 |
15,9 |
15,9 |
16,1 |
16,3 |
16,3 |
16,3 |
16,4 |
16,5 |
16,9 |
|
17,1 |
17,6 |
17,9 |
18,1 |
18,2 |
18,3 |
18,7 |
18,7 |
19 |
20,3 |
Для построения интервального вариационного
ряда определяем число интервалов по
формуле
![]() .
.
![]() .
Значит,
.
Значит,![]() .
Находим длину интервала:
.
Находим длину интервала:
![]() .
.
![]() - формула, по которой определяются
границы интервалов.
- формула, по которой определяются
границы интервалов.
Составляем расчетную таблицу в виде интервального вариационного ряда.
|
№ ин-тер-вала |
xi; xi+1) |
ci |
ni |
wi |
|
cini |
| |
|
1 |
7,8; 9,88) |
8,84 |
1 |
0,02 |
0,0096 |
8,84 |
78,146 | |
|
2 |
9,88; 11,96) |
10,92 |
11 |
0,22 |
0,1058 |
120,12 |
1311,170 | |
|
3 |
11,96; 14,04) |
13 |
10 |
0,2 |
0,0962 |
130 |
1690 | |
|
4 |
14,04; 16,12) |
15,08 |
12 |
0,24 |
0,1154 |
180,96 |
2728,877 | |
|
5 |
16,12; 18,2) |
17,16 |
11 |
0,22 |
0,1058 |
188,76 |
3239,122 | |
|
6 |
18,2; 20,3 |
19,25 |
5 |
0,1 |
0,0481 |
96,25 |
1852,81 | |
|
Сумма |
50 |
1 |
|
S1=724,93 |
S2=10900,125 | |||
![]() - середина интервала;
- середина интервала;![]() - значения частот;
- значения частот;
![]() - относительная частота.
- относительная частота.
2) Строим гистограмму относительных частот.
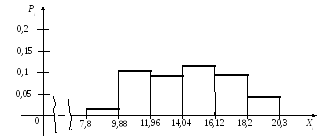
Эмпирическая функция распределения
выборки
![]() находится по формуле:
находится по формуле:
![]() ,
,
где
![]() - число вариант, меньшихx.
- число вариант, меньшихx.
Строим эмпирическую функцию распределения.
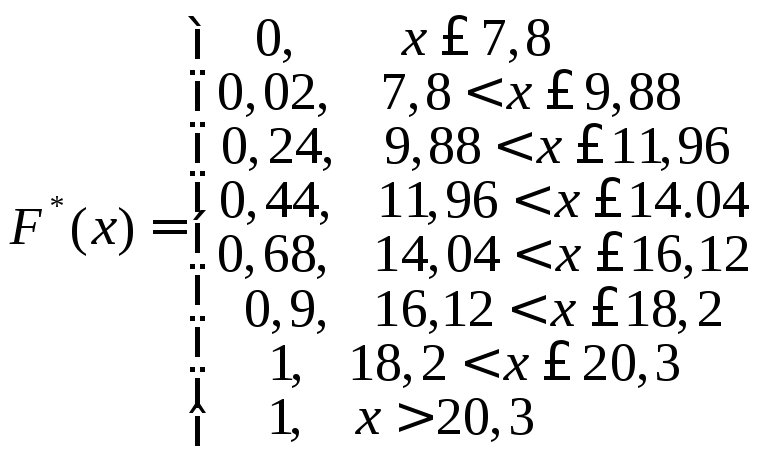
Строим график эмпирической функции распределения (кумулянту).

3) Определяем выборочную среднюю
![]() по формуле
по формуле![]() .
.
![]()
Находим выборочную дисперсию
![]() по формуле
по формуле![]() .
.
![]() .
.
Находим среднее квадратическое отклонение
![]() .
.
Для определения моды
![]() ,
сначала выбираем модальный интервал с
наибольшей частотой.
,
сначала выбираем модальный интервал с
наибольшей частотой.
В нашем случае это 4-й интервал.
Моду находим по следующей формуле:
![]() ,
где
,
где![]() - начальная граница модального интервала;
- начальная граница модального интервала;
![]() - частота модального интервала;
- частота модального интервала;
![]() - частота предмодального интервала;
- частота предмодального интервала;
![]() - частота послемодального интервала;
- частота послемодального интервала;
- длина интервала.
![]() .
.
Для определения медианы находим медианный интервал. Проверяем по порядку следующие условия:
![]()
![]()
![]()
В нашем случае 4-й интервал является медианным.
Медиану
![]() находим по формуле:
находим по формуле:
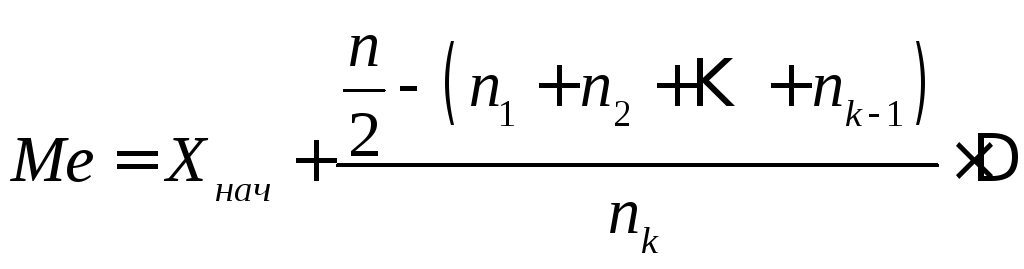 ,
где
,
где![]() - начальная граница медианного интервала;
- начальная граница медианного интервала;
![]() - частота медианного интервала;
- частота медианного интервала;
![]() - объем выборки;
- объем выборки;
![]() - сумма частот до медианного интервала;
- сумма частот до медианного интервала;
- длина интервала.
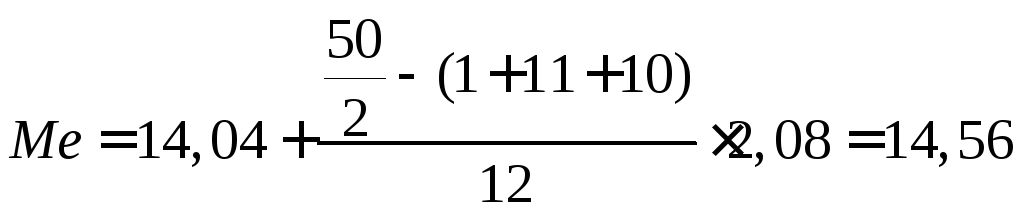 .
.
