UnEncrypted

Aguiar et al.

infection. γ is the recovery rate, μ is the demographic rate, α is the waning immunity rate related to temporary cross-immunity, and φ is the ADE ratio which describes the secondary infection contribution to the force of infection. In the models the ADE e ect modifies the transmissibility of secondary infections. When φ is larger than one, individuals in their secondary infection transmit the disease more than individuals in their first infection, and when φ is smaller than one, the individuals in their secondary infection are transmitting less than individuals in their first infection. The parameter ρ is the import factor, related to the possibility of an individual to get infected outside the studied population and then bring the infection into the population to which this individual belongs to, mimicking the imported cases of the disease in a defined population.

Dengue models including multi-strain interactions via ADE but without temporary cross-immunity period e.g. [18, 19, 20] have shown deterministic chaos when strong infectivity on secondary infection was assumed.

Figure 2: Bifurcation diagram. In a) model neglecting temporary cross-immunity (α = 52y−1). In b) model assuming temporary cross-immunity (α = 2y−1).

The di erent forces of infection combined with the temporary cross immunity period bring complex behavior in a unexpected and biologically more realistic parameter region,

φ> 1 [5, 6, 3], i.e. deterministic chaos was found in a wider parameter regions. In Fig. 2 we show bifurcation diagrams were the total number of infected individuals in a log scale is plotted over the ADE ratio parameter. Fixed points appear as one dot per parameter value, limit cycles appear as two dots, double-limit cycles as four dots, more complicated limit cycles as more dots, and chaotic attractors as continuously distributed dots for a single

φvalue. We see that when temporary cross immunity is assumed, a new chaotic window appears, and the ADE e ect does not need to be restricted to one or another region in

Descriptive and Predictive models of dengue epidemiology

parameter space.

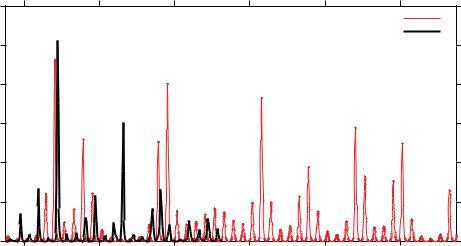
The seasonal model with import shows complex dynamics and qualitatively a very good result when comparing empirical DHF and simulations (see Fig. 3) [3]. However, the extended model needs to be parametrized on data referring to incidence of severe disease.

A qualitatively a very good result when comparing empirical DHF data and simulation suggest that this parameter set could be the starting set for a more detailed parameter estimation procedure. In Fig. 3 the model simulation is matched with the DHF data for the Chiang Mai province in Thailand.

time (years)

Figure 3: For the following parameter set: β0 = 2γ, γ = 52y−1, α = 2y−1, φ = 0.9 and μ = 1/65y−1 empirical DHF incidence data (in black) for the province of Chiang Mai in the North of Thailand are matched with simulations (in red) for the seasonal multi-strain models with import of infected. The parameter β is given explicitly by β(t) = β0 ·(1+η ·cos(ω ·t)) where β0 is the infection rate and η is the degree of seasonality. Here, the degree of seasonality is η = 0.35 and the import factor ρ = 10−10.

However, more stochasticity is needed to get even better agreement for some of the available data sets, as in the case for Bangkok, where the available data is very noisy linked with a low endemicity of DHF cases [29].

The two-strain model in its simplicity is a good model to be analyzed, giving the expected complex behavior to explain the fluctuations observed in empirical data. It is minimalistic in the sense that it can capture the essential di erences of primary versus

Aguiar et al.

secondary infection without needing to restrict the ADE e ect to one or another region in parameter space. For future parameter estimation only the two-strain model could attempt to estimate all initial conditions as well as the few model parameters.

3Prospective work and discussion

In this manuscript we presented the o cial notification DHF data from the Ministry of Public Health in Bangkok, Thailand. The representation of the biological processes using mathematical modeling approach were improved in comparison to previous models based on the following aspects: temporary cross-immunity, antibody dependent enhancement, and seasonality. We now propose to extend the previously existing dengue models, by including vector dynamics, and the transmission contribution of an asymptomatic host and data analysis.

A model which can be fully parametrized on data referring to incidence of disease can become a predictive tool to guide the policies of prevention and control of the dengue virus transmission, including the implementation of vaccination programs when the candidate dengue fever vaccines will be available.

After the expansion of previous multi-strain dengue models, the basic parameters of transmission, infectivity and disease severity (ADE parameter) will be a ected. In such a way the model will be parametrized on data referring to incidence of severe disease and prevalence of infection from di erent endemic countries with di erent intensities of dengue transmission. Technical parameter estimation is notoriously di cult for chaotic time series but temporally local approaches are possible [27], for example. In the EU project Dengue Research Framework for Resisting Epidemics in Europe (DENFREE), with a work-package on descriptive and predictive models of dengue epidemiology, various sources of data will be accessed to test the models which are able to provide a valuable tool to guide policies of prevention and control of the dengue virus transmission.

Acknowledgements

This work has been supported by the EU project DENFREE under Framework Program 7 and has been further supported by the Portuguese FCT project PTDC/MAT/115168/2009. We thank Bernard Cazelles, Ecole Normale Sup´erieure, France, and Yoshiro Nagao, Osaka University Graduate School of Medicine in Japan, for enabling us with parts of the existing data sets for Thailand prior to our access of the full data in collaboration with the MoPh in Bangkok.

Descriptive and Predictive models of dengue epidemiology

References

[1]World Health Organization. (2009). Dengue and Dengue Hemorrhagic Fever, Fact sheet 117. Retrieved from http://www.who.int/mediacentre/factsheets/fs117/en/

[2]World Health Organization – Programs and Projects: Initiative for Vaccine Research (2011). Vector borne infections. Retrieved from

http://www.who.int/vaccine research/diseases/vector/en/index1.html#virology

[3]Aguiar, M., Ballesteros, S., Kooi, B.W., & Stollenwerk, N. (2011) The role of seasonality and import in a minimalistic multi-strain dengue model capturing di erences between primary and secondary infections: complex dynamics and its implications for data analysis, Jounal of Theoretical Biology, 289, 181–196.

[4]Stollenwerk, N., Aguiar, M., Ballesteros, S., Boto, J., Kooi, W. B., & Mateus, L. (2012). Dynamic noise, chaos and parameter estimation in population biology, Interface Focus, 2, 156–169.

[5]Aguiar, M., Kooi, B., & Stollenwerk, N. (2008) Epidemiology of dengue fever: A model with temporary cross-immunity and possible secondary infection shows bifurcations and chaotic behaviour in wide parameter regions, Math. Model. Nat. Phenom. 3, 48–70.

[6]Aguiar, M., Stollenwerk, N., & Kooi, B. (2009) Torus bifurcations, isolas and chaotic attractors in a simple dengue fever model with ADE and temporary cross immunity,

Intern. Journal of Computer Mathematics 86, 1867–77.

[7]Wikipedia contributors. Wikipedia, The Free Encyclopedia. Provinces of Thailand. Retrieved from http://en.wikipedia.org/wiki/Provinces of Thailand

[8]Halstead S. B., et al. (1969). Dengue and chikungunya virus infection in man in Thailand, 1962–1964. V. Epidemiologic observations outside Bangkok. Am. J. Trop. Med. Hyg. 18, 1022–33.

[9]Gubler D. J., (2002). Epidemic dengue/dengue hemorrhagic fever as a public health, social and economic problem in the 21st century. Trends in Microbiology, 10, 100–103.

[10]Chareonsook, O.et al. (1999). Changing epidemiology of dengue hemorrhagic fever in Thailand. Epidemiol. Infect., 122, 161–166.

[11]S. Matheus, X. Deparis, B. Labeau, J. Lelarge, J. Morvan, P. Dussart. Discrimination between Primary and Secondary Dengue Virus Infection by an Immunoglobulin G Avidity Test Using a Single Acute-Phase Serum Sample. Journal of Clinical Microbiology (2005), No. 43, 2793–97.

Aguiar et al.

[12]Dejnirattisai, W. et al. (2010). Cross-Reacting Antibodies Enhance Dengue Virus Infection in Humans. Science, 328, 745–748.

[13]Guzm´an, M.G. et al. (2010). Dengue: a continuing global threat. Nature Reviews Microbiology, 8, S7–S16, ISSN : 1740-1526.

[14]Halstead, S.B. (1982). Immune enhancement of viral infection. Progress in Allergy, 31, 301–364,ISSN 0079-6034.

[15]Halstead, S. B. (1994). Antibody-dependent Enhancement of Infection: A Mechanism for Indirect Virus Entry into Cells. Cellular Receptors for Animal Viruses, 28, Chapter 25, 493–516, ISBN 0-87969-429-7. (Cold Spring Harbor Laboratory Press).

[16]Halstead, S.B. (2003). Neutralization and antibody-dependent enhancement of dengue viruses. Advances in Virus Research, 60, 421–467.

[17]Mackenzie, J. S., Gubler, D. J. & Petersen, L. R. (2004). Emerging flaviviruses: the spread and resurgence of Japanese encephalitis, West Nile and dengue viruses. Nature Medicine Review, 12, S98–S109.

[18]Ferguson, N., Anderson, R. and Gupta, S. (1999). The e ect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens.

Proc. Natl. Acad. Sci. USA, 96, 790–94.

[19]Schwartz, I. B., et al. (2005). Chaotic desynchronization of multi-strain diseases. Physical Review, E 72, 066201–6.

[20]Billings, L., et al. (2007). Instabilities in multiserotype disease models with antibodydependent enhancement. Journal of Theoretical Biology, 246, 18–27.

[21]Wearing, H.J. & Rohani, P. (2006). Ecological and immunological determinants of dengue epidemics Proc. Natl. Acad. Sci. USA , 103, 11802–11807.

[22]Nagao, Y. & Koelle, K.(2008). Decreases in dengue transmission may act to increase the incidence of dengue hemorrhagic fever. Proc. Natl. Acad. Sci. USA, 105, 2238–2243.

[23]Recker, M. et al. (2009). Immunological serotype interactions and their e ect on the epidemiological pattern of dengue. Proc. R. Soc. B., 276, 2541–2548.

[24]Map of Thailand. Retrieved from http://thethailandlife.com/map-of-thailand

[25]Ionides, E., Breto, C., & King, A. A. (2006). Inference for nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA, 103, 18438–18443. (DOI:10.1073.pnas.0603181103.)

Descriptive and Predictive models of dengue epidemiology

[26]He, D., Ionides, E. L., King, A. A. (2010). Plug-and-play inference for disease dynamics: measles in large and small populations as a case study. J. R. Soc. Interface, 7, 271–283. (DOI:10.1098/rsif.2009.0151)

[27]Stollenwerk, N., Aguiar, M., Ballesteros, S., Boto, J., Kooi, W. B., Mateus, L. (2012). Dynamic noise, chaos and parameter estimation in population biology. Interface Focus, 2, 156–169.

[28]Aguiar, M., Kooi, W. B., Rocha, F., Gha ari, P. and Stollenwerk, N. (2012). How much complexity is needed to describe the fluctuations observed in dengue hemorrhagic fever incidence data? submitted. Available at arXiv:1111.3844v2 [nlin.CD]

[29]Aguiar, M., Kooi B. W. & Stollenwerk N. (2012). Scaling of stochasticity in DHF epidemics, accepted for publication in MMNP.

Proceedings of the 12th International Conference on Computational and Mathematical Methods in Science and Engineering, CMMSE 2012 July, 2-5, 2012.

Dynamics of some Parallel Dynamical Systems over Digraphs

Juan A. Aledo1, Silvia Martinez1 and Jose C. Valverde1

1 Department of Mathematics, University of Castilla-La Mancha

emails: JuanAngel.Aledo@uclm.es, Silvia.MSanahuja@uclm.es,

Jose.Valverde@uclm.es

Abstract

In a previous research, for parallel dynamical systems over digraphs corresponding to the simplest Boolean functions AND and OR, we proved that only fixed or eventually fixed points appear, as occurs over undirected dependency graphs. Nevertheless, for general Boolean functions, it was shown that any period can appear, depending on the Boolean function that infers the global evolution operator of the system and on the structure of the dependency digraph. In this sense, this work analyzes the orbit structure of parallel discrete dynamical systems over some special digraph classes.

Key words: Discrete dynamical systems; periodic orbits; parallel dynamical systems; directed graphs; Boolean functions.

MSC 2000: 37B99; 37E15; 37N99; 68R10; 94C10.

1Introduction

In the last decade, several works have been dealt with the development of mathematical foundations for a theory of simulation. The first one of a series of these works was [3], where sequentially updated cellular automata (sCA) over arbitrary graphs are employed as a paradigmatic framework. This first step was followed by [4], [5] and [6], where the authors developed this theory, analyzing the asymptotic behavior.

Computer simulations involve generation of dynamics by iterating local mappings. These processes have been usually modeled by cellular automaton. Wolfram [17] analyzed a set of cellular automata and showed that, despite their simple construction, some of them are capable of complex behavior. Later, based on a deeper research [18], he suggested that

Dynamics of Some Parallel Dynamical Systems over Digraphs

many one-dimensional cellular automata fall into four basic behavior classes: three of them exhibiting a similar behavior to fixed points, periodic orbits and chaotic attractors and the fourth one so that asymptotic properties are undecidable. The concept of parallel dynamical system generalizes the one of the cellular automaton.

For convenience, it is common to rename the local mappings as entities (cells in the language of cellular automata theory), which are the lowest level of aggregation of the system. In many processes, there are many entities and each entity has a state at a given time (see [3, 4, 5]). The update of states of the entities constitutes an evolution in time of the system, i.e., a discrete dynamical system (see [7, 13]).

The update of the states is determined by dependency relations of the entities and local rules, which together constitute the (global) evolution operator of the dynamical system (see [12], [16]). If the states of the entities are updated in a parallel (or synchronous) manner, the system is called a parallel dynamical system (PDS), while if they are updated in a sequential order, the system is named sequential dynamical system (SDS) [7, 13, 14].

In particular, in [7] parallel and sequential dynamical systems are studied, considering OR (resp. AND) and NOR (resp. NAND) as global functions. Following these ideas, in [1] we extend these results for the parallel case, giving a complete characterization of the orbit structure of any parallel dynamical system with any maxterm (resp. minterm) as a global function. As a result, for the simplest maxterm (resp. minterm), OR (resp. AND), only fixed or eventually fixed points can appear, while for a general maxterm (resp. minterm), uniquely periodic or eventually periodic orbits of period lower than or equal to 2 can be found.

The results in [1] opened new di erent research directions concerning parallel dynamical systems on Boolean functions. One of them consists in considering non-reciprocal relations between two related entities, because it could occur that an entity influences another one, but not vice versa, as happens in practice [8]. This can be modeled by a directed dependency graph or dependency digraphs of relations.

These non-reciprocal relations emerge also in other applied models created for the simulation of aspects of the behavior of biological systems. This occurs in [10], where Kau man constructed molecular automata for modeling a gene as a binary (on-o ) device and studied the behavior of large, randomly constructed nets of these binary genes (see also [11]). A Kau man net of size n and connectivity k consists of n interconnected vertices, each one having k inputs and one output. The update of any gene is determined by the (directed) dependency relations and local rules which are given by random Boolean functions.

In computer simulation, entities are related and they get information from the related ones in their own neighborhood. In order to get a graphical idea of the situation, every entity is usually represented by a vertex of an undirected graph and two vertices are adjacent if their states influence each other in the update of the system. The undirected graph so built is called the (undirected) dependency graph of the system (see [7]).

J.A. Aledo, S. Martinez, J.C. Valverde

However, as we said before, it could occur that an entity influences another one, but not vice versa. Actually, in practice, the process of information exchange is not bidirectional [8]. This could be represented by an arc whose initial vertex would be the influencing entity and the final vertex would correspond to the influenced entity, so obtaining a directed graph or digraph of relations. The directed graph so built will be called the directed dependency graph of the system.

We actually determine a dynamical system over a directed dependency graph (see [15] for a similar approach that considers cellular automata over Cayley graphs) by associating to each vertex i, a state xi {0, 1} and a local map fi defined on the states of the influencing vertices and the vertex/entity i, and which returns its new state yi {0, 1}. We shall denote this digraph D = (V, A), where V = {1, 2, . . . , n} is the vertex set and A is the arc set.

For every vertex/entity 1 ≤ i ≤ n, we shall consider all the vertices that influence it in an update of the system. Thus, we denote

ID(i) = {j V |(j, i) A}

The evolution or update of the system is implemented by local functions which are the restrictions of a global one. In this context, for updating the state of an entity i, the corresponding local function acts only on the state of that entity itself and the states of the entities in ID(i) which influence i.

Actually, it can be stated the following definition.

Definition Let D = (V, A) be a digraph on V = {1, 2, . . . , n}. Then a map

F : {0, 1}n → {0, 1}n, F (x1, x2, . . . , xi, . . . , xn) = (y1, y2, . . . , yi, . . . , yn),

where yi is the updated state of the entity/vertex i by applying a local function fi over the states of the entities in {i} ID(i), constitutes a discrete dynamical system called parallel directed dynamical system over {0, 1}n.

In this work, the global evolution operator F of the system will be induced by Boolean functions. A Boolean function describes how to determine a Boolean output from some Boolean inputs. Thus, such functions play a fundamental role in questions as design of circuits or computer processes [9]. In our context, they correspond to components of the evolution operator of the dynamical system.

In a previous paper [2], for parallel dynamical systems over digraphs corresponding to the simplest Boolean functions AND and OR, we proved that only fixed or eventually fixed points appear, as occurs over undirected dependency graphs. Nevertheless, for general Boolean functions, it was shown that any periodic orbit can exist, depending on the Boolean function that infer the global evolution operator of the system and on the structure of the dependency digraph. In this sense, this work analyze the orbit structure of parallel discrete dynamical systems over some special digraph classes, as complete, circle, line, star graphs and arborescences.

Dynamics of Some Parallel Dynamical Systems over Digraphs

Acknowledgements

This work has been partially supported by the grants MTM2011-23221, PEII11-0132-7661 and PEII09-0184-7802.

References

[1]J.A. Aledo, S. Martinez and J.C. Valverde, Parallel Dynamical Systems on Maxterms and Minterms Boolean Functions, Math. Comput. Model. 35 (2012) 666– 671.

[2]J.A. Aledo, S. Martinez and J.C. Valverde, Parallel Dynamical Systems over directed dependency graphs, (under review).

[3]C.L. Barret and C.M. Reidys, Elements of a theory of computer simulation I, Appl. Math. Comput. 98 (1999) 241–259.

[4]C.L. Barret, H.S. Mortveit and C.M. Reidys, Elements of a theory of computer simulation II, Appl. Math. Comput. 107 (2002) 121–136.

[5]C.L. Barret, H.S. Mortveit and C.M. Reidys, Elements of a theory of computer simulation III, Appl. Math. Comput. 122 (2002) 325–340.

[6]C.L. Barrett, H.S. Mortveit, C.M. Reidys, ETS IV: sequential dynamical systems: fixed points, invertibility and equivalence, Appl. Math. Comput. 134 (2003) 153171.

[7]C.L. Barret, W.Y.C. Chen and M.J. Zheng, Discrete dynamical systems on graphs and Boolean functions, Math. Comput. Simul. 66 (2004) 487–497.

[8]W.Y.C. Chen, X. Li and J. Zheng, Matrix method for linear sequential dynamical systems on digraphs, Appl. Math. Comput. 160 (2005) 197212.

[9]O. Colon´ -Reyes, R. Laubenbacher, B. Pareigis, Boolean monomial dynamical systems, Ann. Combin. 8 (2004) 425–439.

[10]S. A. Kauffman, Metabolic stability and epigenesis in randomly constructed genetic nets, J. Theor. Biol. 22 (1969) 437–467.

[11]S. A. Kauffman, Origins of Order: Self-Organization and Selection in Evolution, Oxford University Press, Oxford, 1993.

[12]Y.A. Kuznetsov, Elements of Applied Bifurcation Theory, Springer, New York, 2004.