
- •2012 Введение
- •Неопределённый интеграл (блок-схема)
- •Оглавление
- •Глава 1. Первообразная и неопределённый интеграл
- •1.1. Определение первообразной функции
- •1.4. Следствия из теоремы «единственности» первообразной
- •1.5. Неопределённый интеграл
- •Операция интегрирования – операция нахождения
- •1.6. Проблема существования первообразной
- •1.7. Геометрическая интерпретация первообразной
- •1.8. Простейшее дифференциальное уравнение. Задача Коши
- •1.9. Проблема нахождения первообразной
- •1.10 Табличные интегралы
- •1.11. Неберущиеся интегралы
- •1.12. Линейные свойства неопределённого интеграла
- •1.13. Дифференциал неопределённого интеграла
- •1.14. Неопределённый интеграл от дифференциала
- •1.15. Непосредственное интегрирование
- •1.16. Метод замены переменной. Основные теоремы
- •Формулы интегрирования сохраняют свою структуру
- •1.17. Замена переменной. Способ 1.
- •1.18. Замена переменной в интеграле. Способ 2
- •1.19. Интегрирование по частям
Глава 1. Первообразная и неопределённый интеграл
1.1. Определение первообразной функции
Поставим задачу:
требуется найти функцию
![]() такую, что
такую, что![]() .
.
Решение этой
задачи очевидно: функция
![]() есть искомая функция.
есть искомая функция.
Решение не
единственно,
поскольку
![]() ,
,![]() ,
,![]() и т.д.
и т.д.
Данная задача – задача восстановления функции по её производной.
Функция
![]() –первообразная
функция (или первообразная)
для функции
–первообразная
функция (или первообразная)
для функции
![]() .
Любая функция из множества
.
Любая функция из множества![]() ,
где
,
где![]() -
произвольная постоянная, тоже является
первообразной для функции
-
произвольная постоянная, тоже является
первообразной для функции![]() .
.
Введём определение первообразной функции.
Определение
1.1. Пусть
на промежутке
![]() определены функции
определены функции![]() и
и![]() ,
и во всех точках этого промежутка имеет
место равенство
,
и во всех точках этого промежутка имеет
место равенство
-

(1.1)
Тогда говорят, что
функция
![]() естьпервообразная
функция,
или просто первообразная
функции
естьпервообразная
функция,
или просто первообразная
функции
![]() на промежутке
на промежутке![]() .
.
Примеры 1.1.
1.
Функция
![]() - первообразная функции
- первообразная функции![]() на промежутке
на промежутке![]() ,
поскольку
,
поскольку![]() во всех точках числовой оси.
во всех точках числовой оси.
2.
Функция
![]() - первообразная функции
- первообразная функции![]() на промежутке
на промежутке![]() ,
поскольку
,
поскольку![]() во всех точках этого промежутка.
во всех точках этого промежутка.
3.
Функция
![]() - первообразная функции
- первообразная функции![]() на интервале
на интервале![]() ,
поскольку
,
поскольку![]() всюду на интервале
всюду на интервале![]() .
.
так,
|
|
|
|
Проблемы, связанные с определением первообразной
Перечислим три основные проблемы, связанные с определением первообразной.
1. Проблема существование первообразной:
какие функции имеют первообразную?
2. Проблема единственности первообразной:
если первообразная существует, единственна она или нет?
3. Проблема нахождения первообразной:
если первообразная данной функции существует, то как её найти?
Проблема единственности первообразной
Ответ на вопрос о
единственности первообразной несложен.
Напомним, что задача, поставленная в п.
1.1, решается неоднозначно: функция
![]() имеет бесконечное множество
имеет бесконечное множество![]() первообразных функций. Здесь
первообразных функций. Здесь![]() - произвольная постоянная на всей
числовой прямой функции.
- произвольная постоянная на всей
числовой прямой функции.
В общем случае,
если
![]() - первообразная функция
- первообразная функция![]() на промежутке
на промежутке![]() ,
то любая функция из множества
,
то любая функция из множества![]() ,
где
,
где![]() - произвольная постоянная на промежутке
- произвольная постоянная на промежутке![]() функция (или просто постоянная), тоже
является первообразной функции
функция (или просто постоянная), тоже
является первообразной функции![]() на этом промежутке, поскольку
на этом промежутке, поскольку![]() .
.
Итак,
-
 –первообразная
–первообразнаяфункции
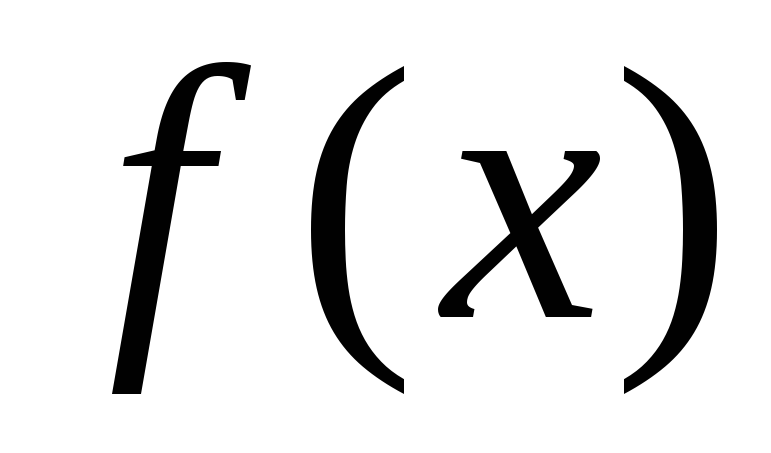

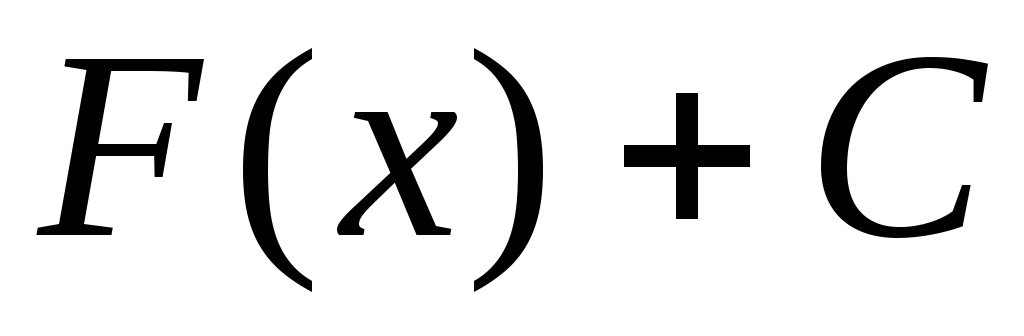 –первообразная
функции
–первообразная
функции
 ,
,
Другими словами, если данная функция имеет первообразную, то фактически эта функция имеет бесконечно много «однотипных» первообразных функций, графики которых могут быть построены с помощью одного шаблона.
Возникает вопрос:
может ли функция
![]() иметь первообразную, не входящую в
бесконечное множество
иметь первообразную, не входящую в
бесконечное множество![]() её первообразных? Ответ на этот вопрос
даёт следующая теорема.
её первообразных? Ответ на этот вопрос
даёт следующая теорема.
Теорема
1.1.
(«Единственность»
первообразной). Если
![]() –
–
одна из первообразных
функций для функции
![]() на промежутке
на промежутке![]() ,
то любая первообразная
,
то любая первообразная![]() функции
функции![]() на промежутке
на промежутке![]() имеет вид
имеет вид![]() ,
где
,
где![]() -
некоторая постоянная на промежутке
-
некоторая постоянная на промежутке![]() функция.
функция.
Доказательство.
Введём
функцию
![]() Функция
Функция
![]() дифференцируема на промежутке
дифференцируема на промежутке![]() как разность двух дифференцируемых
функций, причём, всюду на
как разность двух дифференцируемых
функций, причём, всюду на![]()
![]()
![]()
Тогда в силу
следствия из теоремы Лагранжа функция
![]() постоянна на промежутке
постоянна на промежутке![]() ,
т.е.
,
т.е.![]() ,
или
,
или![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Итак, если
![]() - первообразная функции
- первообразная функции![]() на промежутке
на промежутке![]() ,
то множество всех её первообразных
совпадает с множеством
,
то множество всех её первообразных
совпадает с множеством![]() ,
где
,
где![]() - произвольная постоянная на промежутке
- произвольная постоянная на промежутке![]() функция.
функция.![]()
Итак, первообразная данной функции на данном промежутке единственна с точностью до постоянного слагаемого.

